Centre of Mass | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Introduction |

|
| Centre of Mass |

|
| Centre of Mass of a Continuous Mass Distribution |

|
| Centre of Mass After Partial Removal |

|
| Motion of Centre of Mass |

|
Introduction
- Imagine balancing a pencil on your finger—there’s a special spot where it stays balanced. This is its centre of mass, the point where all of its weight seems concentrated.

- Every object, no matter its size or shape, has a center of mass, which helps us predict how it moves.
- In physics, understanding the centre of mass simplifies studying motion, making it easier to analyze the movement of anything from a car to a spinning basketball.
What is a Rigid Body?
Objects that don’t change shape when force is applied are called rigid bodies.
- When discussing the center of mass, we looked at different types of objects made up of millions of tiny particles.
- Some of these objects can change shape or get deformed when a force is applied to them. Objects that don’t change shape when force is applied are called rigid bodies.
- So, rigid bodies are those that don't deform under stress, and their center of mass stays in the same place.
- For rigid bodies with uniform density, the center of mass is usually at the geometric center (centroid).
- Examples of rigid bodies include solid steel spheres and solid cylinders.
Centre of Mass
- When we look at a group of moving particles as a whole, we don't have to worry about each particle's movement. Instead, we can just focus on one special point that represents the entire group.
- This point is called the centre of mass. The motion of this point is just like the motion of a single particle, but its mass is the total mass of all the particles in the group.
- For objects that have the same density throughout and are solid, the center of mass is at the object's geometric center. For instance, in a disc with even thickness, the center of mass is at the middle. However, the center of mass isn't always on the object itself. In the case of a ring, the center of mass is in the center of the ring, where there’s no actual material.
 Centre of mass concentrated at one point
Centre of mass concentrated at one point
- The forces acting on all the particles can be thought of as acting directly on this centre of mass.
- It is a useful concept for understanding how groups of objects move together, particularly during events such as collisions or explosions.
- So, instead of dealing with the complexity of each particle's movement, we simplify things by thinking about the motion of the centre of mass.
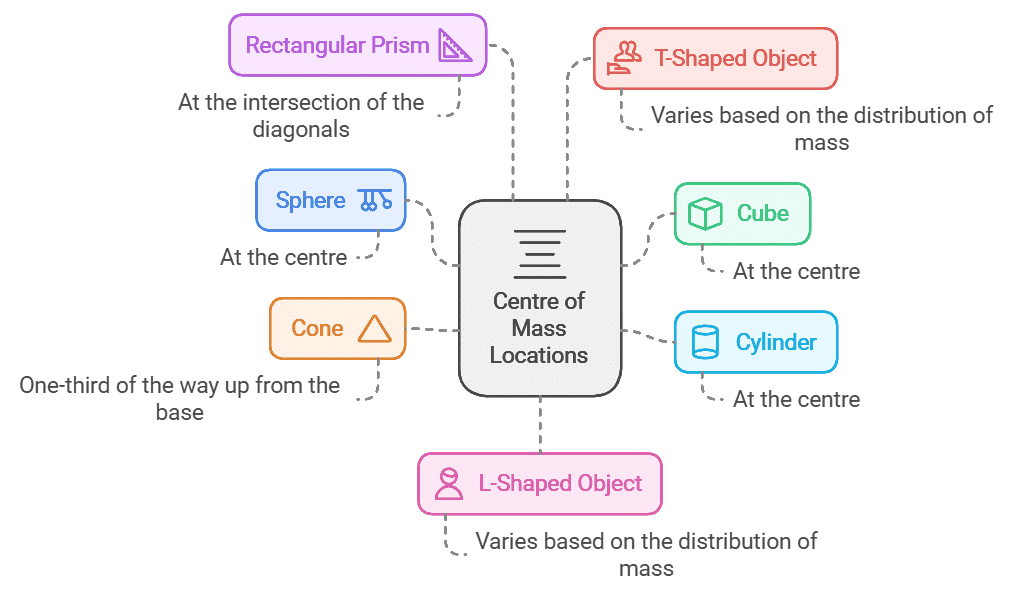
Centre of Mass for Various Objects
The center of mass for certain 3D solids is as follows:
Centre of Mass of a System of 'n' Particles
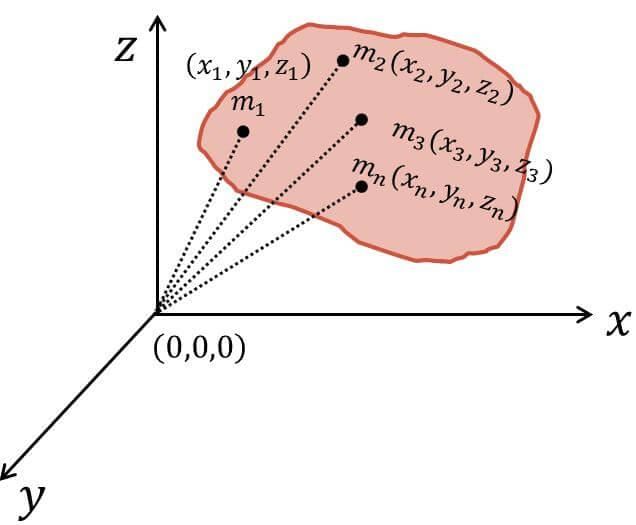
Consider a system of n particles as shown in the figure below, having masses m1, m2, m3, .................. mn and their position vectors 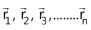 respectively. The position vector of the centre of mass is rcm with respect to the origin,
respectively. The position vector of the centre of mass is rcm with respect to the origin,
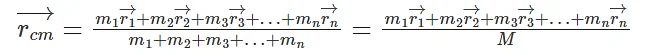
Here,
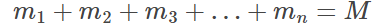
M is the total mass of the system.
If the total mass of the system is M, then 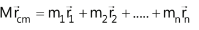
 System of ParticlesFurther,
System of ParticlesFurther, 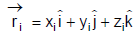
So, the cartesian coordinates of centre of mass will be,
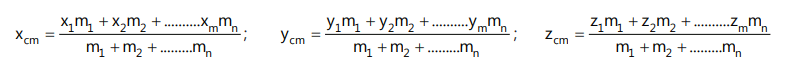
If the origin is taken at the centre of mass then
= 0. hence, the centre of mass is the point about which the sum of "mass moments" of the system is zero.
If we change the origin, then
changes. So
also changes but exact location of center of mass does not change.
Examples of Centre of Mass Motion
- The Earth moves around the Sun in an elliptical orbit, while the Moon revolves around the Earth in a circular orbit. Both the Earth and the Moon move around a common center of mass.
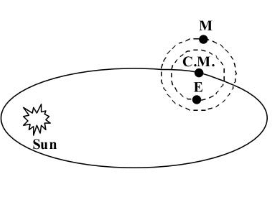
The gravitational attraction between the Earth and the Moon is the internal force acting on this system. The Earth and Moon are always positioned on opposite sides of this center of mass. Since the Earth is much heavier than the Moon, the centre of mass of the Earth-Moon system is located very close to the Earth. This center of mass revolves around the Sun in an elliptical path.
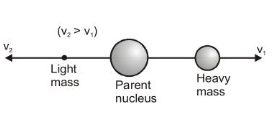
- In radioactive decay, the process happens due to the internal forces within the system. Because of this, the initial and final momentum are both zero. As a result, the decay products move in opposite directions. The centre of mass of the system stays at rest. The heavier particle moves more slowly compared to the lighter particle.
- When a projectile (like a firecracker) explodes in mid-air, it initially follows a parabolic path due to gravity. After the explosion, each piece moves on its own parabolic path, but the centre of mass of the projectile continues along the same original parabolic path.

Explanation: The projectile moves in a parabolic path under the influence of Earth's gravity. When the projectile explodes, it's due to internal forces within the system, and there is no external force acting on it. These internal forces change the momentum of individual fragments, but they do not change the total momentum of the system. Therefore, the centre of mass remains unaffected and continues to follow the same parabolic path as it did before the explosion.
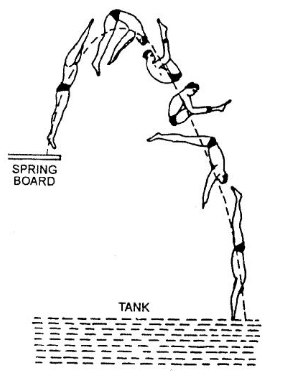
- When a diver jumps into water from a height, their body can move in different directions, but the centre of mass of their body follows a parabolic path. This shows that the centre of mass follows the laws of motion.
Position of Centre of Mass of Two Particles
For a system comprising of two particles of masses m1 and m2, positioned at coordinates (x1, y1, z1) and (x2, y2, z2), respectively, we have:
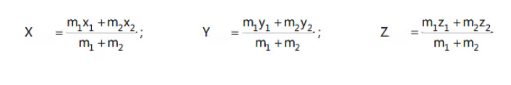 For a two-particle system, Centre of mass lies closer to the particle having more mass, which is rather obvious. If centre of mass coordinates are made zero, we would observe that the distances of individual particles are inversely proportional to their masses.
For a two-particle system, Centre of mass lies closer to the particle having more mass, which is rather obvious. If centre of mass coordinates are made zero, we would observe that the distances of individual particles are inversely proportional to their masses.
Q1. Two particles of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.
Sol: For the system of particles of masses m1 and m2 , if the distances of the particles from the centre of mass are r1 and r2 respectively then it is seen that,
m1 r1 = m2 r2
Since both the particles lie on the x-axis, the centre of mass will also lie on the x-axis. Let the centre of mass be located at x = x, then
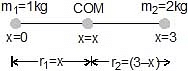
r1 = distance of centre of mass from the particle of mass 1 kg = x,
r2 = distance of centre of mass from the particle of mass 2 kg = (3 -x)
Using
or
or x = 2 m
Thus, the centre of mass of the two particles is located at x = 2m.
Q2. Two particles of mass 4 kg & 2 kg are located as shown in the figure then find out the position of centre of mass.
Sol: First, find out the position of the 2 kg mass
x2kg = 5 cos 37° = 4 m
y2kg = 5 sin 37° = 3 m
So this system is like a two-particle system of mass 4 kg and 2kg are located (0, 0) and (4, 3) respectively, then
x = =
=
=
y = =
= 1 m
So, the position of C.O.M is
Q3. Two particles of mass 2 kg and 4 kg lie on the same line. If 4 kg is displaced rightwards by 5 m then by what distance 2 kg should be moved for which centre of mass will remain at the same position?
Sol: Let us assume that Centre of mass lie at point C and the distance of C from 2 kg and 4 kg particles are r1 and r2 respectively. Then from relation
m1r1 = m2r2
2r1 = 4r2 ...(i)
Now 4 kg is displaced rightwards by 5 m then assume 2 kg is displaced leftwards by x distance to keep the centre of mass at rest.
From relation: m1r1 = m2r2'
⇒ m1(r1 + x) = m2 (r2 + y)
⇒ 2(r1 + x) = 4(r2 + 5) ...(ii)
⇒ 2x = 20
⇒ x = 10 m
Alter: If the centre of mass is at rest then we can write
m1x = m2y
2 × x = 4 × 5
x = 10 m.
Q4. Two particles of mass 1 kg and 2 kg lie on the same line. If 2 kg is displaced 10 m rightwards then by what distance 1 kg be displaced so that the centre of mass will be displaced 2m rightwards?
Sol: Initially let us assume that centre of mass is at point C which is r1 & r2 distance apart from mass m1 & m2 respectively as shown in the figure
From relation: m1 r1 = m2 r2
⇒ (1) r1 = 2 r2
Now 2 kg is displaced 10 m rightwards then we assume that 1 kg is displaced x m leftward to move centre of mass 2m rightwards.
So from relation, m1r1' = m2r2'
⇒ 1 (x + r1 + 2) = 2 (10 + r2 - 2)
⇒ x + r1 + 2 = 20 + 2r2 - 4 ...(ii)
from eq. (i) & (ii)
x = 14 m (leftwards).
Q5. Three particles of mass 1 kg, 2 kg, and 3 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Find the distance of their centre of mass from A.
Sol: Assume that 1 kg mass is placed at the origin as shown in the figure
Coordinate of A = (0, 0)
Coordinate of B = (1 cos60°,1 sin60°) =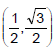
Coordinate of C = (1, 0)
Position of centre of mass
Distance of centre of mass from point
Centre of Mass of a Continuous Mass Distribution
For continuous mass distribution, the centre of mass can be located by replacing the summation sign with an integral sign.
Proper limits for the integral are chosen according to the situation: = M (mass of the body)
here x, y, z in the numerator of the is the coordinate of the centre of mass of the dm mass. =
If an object has symmetric mass distribution about x axis then y coordinate of centre of mass is zero and vice-versa.
Centre of Mass of a Uniform Straight Rod
- Suppose a rod of mass M and length L is lying along the x-axis with its one end at x = 0 and the other at x = L. Mass per unit length of the rod l =
- Therefore, dm, (the mass of the element dx situated at x = x is) = l dx
- The coordinates of the element dx are (x, 0, 0).
- Therefore, the x-coordinate of centre of mass of the rod will be
x ==
=
- The y-coordinate of centre of mass is
y == 0
- Similarly, z = 0
i.e., the coordinates of centre of mass of the rod are, i.e., it lies at the centre of the rod.
Note: Many people mistakenly believe that the centre of mass of a continuous body must be inside the body. However, the centre of mass can be outside the body in specific configurations, such as hollow rings.
Centre of Mass of a Uniform Semicircular Wire
To derive the expression for the coordinates of the centre of mass of a semicircular ring with linear density �σ and radius �r, we can use the method of integration.
- Let's assume that the semicircular ring is in the first quadrant, with the base of the semicircle on the X-axis, and the centre of the equivalent circle placed at the origin of the Cartesian plane as shown in the image below:
 Semicircular ring
Semicircular ring - Consider a small mass element ��dm on the semicircular ring. The mass of this element can be expressed as ��=�⋅��dm = σ⋅ds, where ��ds is the differential arc length.
- The position vector of this mass element ��dm with respect to the centre of the semicircular ring can be expressed as �⃗=�cos(�)�^+�sin(�)�r=r cos(θ)i+r sin(θ)j,
where �θ is the angle made by the position vector with the positive x-axis. - Then, the total mass of the ring is m=σ π r.
- �=���.Let the radius touching this point of the ring make an angle θ with the positive X axis. Consider a small portion of the ring of length ds=rdθ.��=���
- The mass of this portion is dm=σ rdθ.The distance of this portion from the base of the semicircle is, y=rsinθ.
The centre of mass (�cm,�cm)(xcm, ycm) of the semicircular ring can be calculated using the formula:
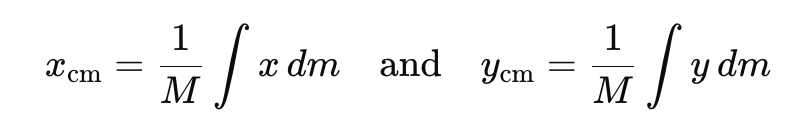
- On substituting the required values we get,
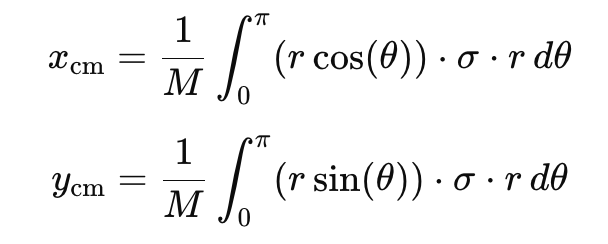
- For x- coordinate:
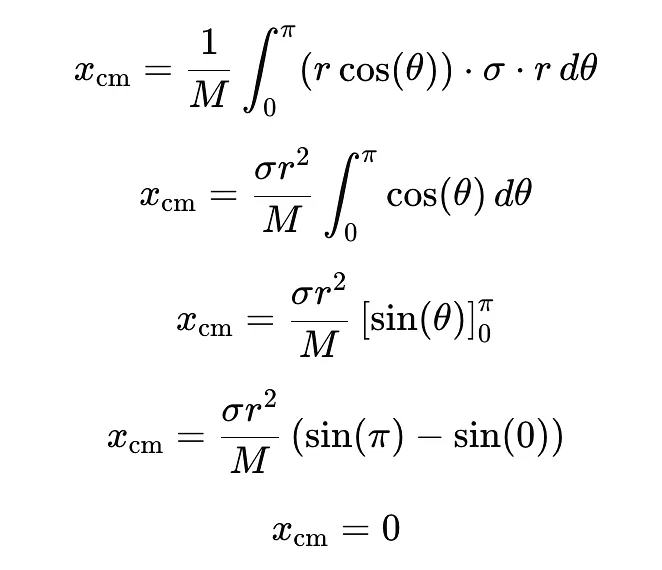
- For y-coordinate:
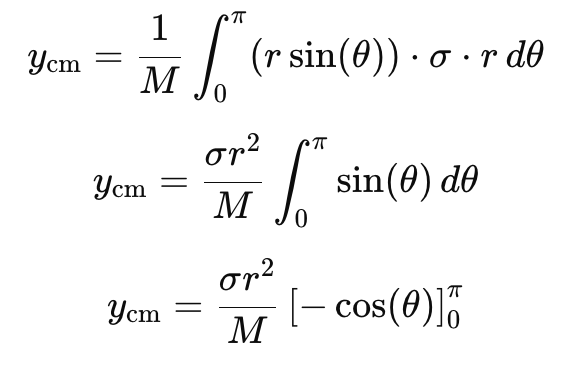
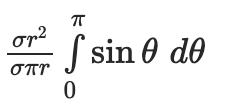
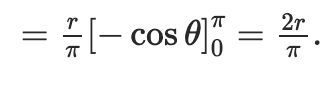
The centre of mass of a uniform semicircular ring of radius r� is (0, 2R/π) , (0,2�where the centre of the equivalent circle is at the origin of the Cartesian plane and the base of the semicircle is on the X-axis.
Centre of Mass of Uniform Semicircular Plate
To derive the expression for the coordinates of the centre of mass of a semicircular plate with radius �r, we can use the method of integration.
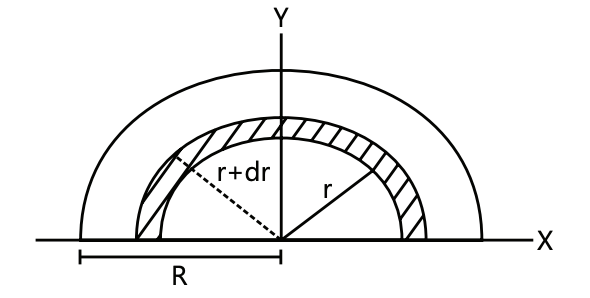 Semicircular Plate
Semicircular Plate
- For a semicircular plate, we'll use polar coordinates for integration. The coordinates of the centre of mass (�ˉ,�ˉ)(x,y) are given by the equations:
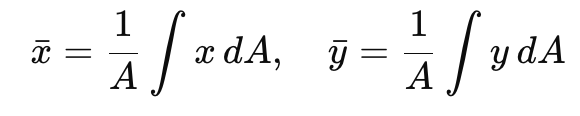
Here �A is the area of the semicircle, and ��dA is an infinitesimal area element of the semicircle.
- In polar coordinates, an element of area ��dA can be represented as � �� ��rdr dθ, where �r is the radius from the origin to the area element, and ��dθ is the differential angle in radians. For a semicircle, �r ranges from 00 to �R, and �θ ranges from 00 to �π.
- The �x coordinate of a point in polar coordinates is given by �=�cos(�)x=r cos(θ).
However, due to symmetry about the �y-axis, we know that for every point with a positive �x, there's a corresponding point with a negative �x of equal mass, making the net �x-coordinate of the centre of mass 00. - The �y coordinate of a point in polar coordinates is �=�sin(�)y=r sin(θ).
Substituting this into the formula for �y, we get: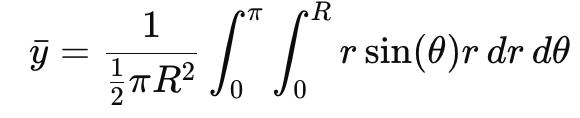 Simplifying, we distribute �r and move constants outside of the integral:
Simplifying, we distribute �r and move constants outside of the integral:
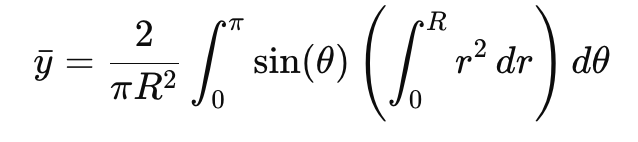
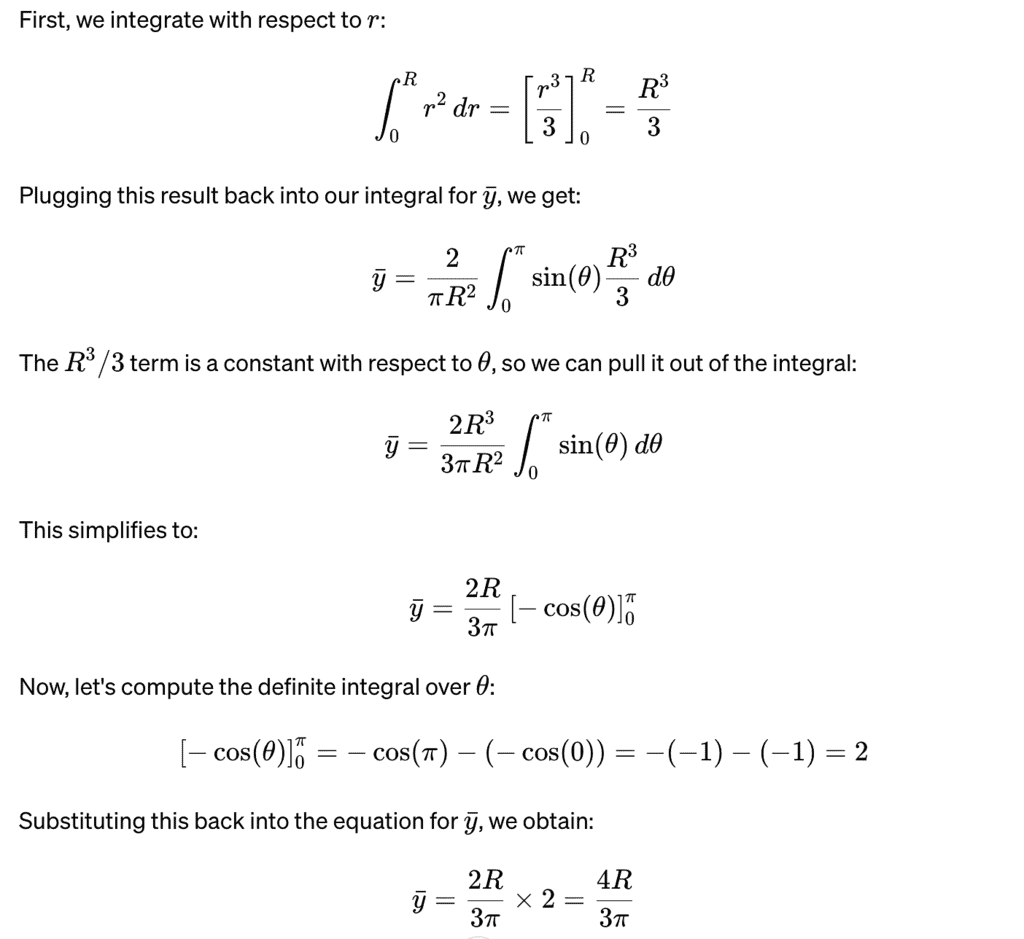
The centre of mass of a uniform semicircular plate of radius R is (0, 4R/3π).
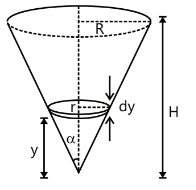
Q1. Determine the centre of mass of a uniform solid cone of height h and semi angle α, as shown in figure.

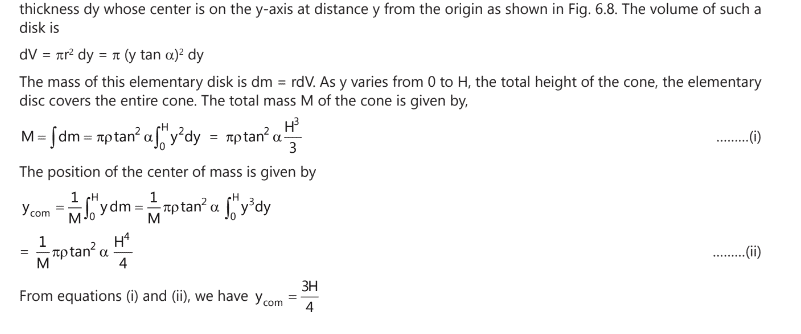
Some Important Figures
Here's a comprehensive table that compiles the values of centre of mass coordinates for all the important figures, in Cartesian coordinates, suitable for objective-type questions in NEET:

- L: Total length of the rod or side length of the rectangle/square.
- W: Width of the rectangle.
- R: Radius of the circle or semicircle.
- b: Base length of the triangle.
- h: Height of the triangle from the base to the opposite vertex.
- H: Height of the cylinder or cone.
Centre of Mass After Partial Removal
- To find the coordinates of the centre of mass of a body after a portion of it is removed, we can consider the body and the removed part as two separate masses and then use the principle of superposition for the centre of mass.
- Let's assume we know the coordinates of the centre of mass of the original body (�original,�originalxoriginal, yoriginal) before any mass is removed and the coordinates of the centre of mass of the removed portion (�1,�1x1,y1).
- The mass of the original body is �m, and the mass of the removed portion is �1m1. The task is to find the coordinates of the new centre of mass of the remaining body (�new,�newxnew,ynew).
 Q1. A rectangular sheet of metal has dimensions of 4 m by 3 m and a uniform mass of 24 kg. A square piece of side 1 m is cut out from one of the corners of the sheet. Find the coordinates of the centre of mass of the remaining sheet if the original centre of mass of the whole sheet was at the geometric centre. Assume the sheet and the cut-out piece have uniform thickness and density.
Q1. A rectangular sheet of metal has dimensions of 4 m by 3 m and a uniform mass of 24 kg. A square piece of side 1 m is cut out from one of the corners of the sheet. Find the coordinates of the centre of mass of the remaining sheet if the original centre of mass of the whole sheet was at the geometric centre. Assume the sheet and the cut-out piece have uniform thickness and density.
Sol:
Dimensions of the rectangular sheet: 4 m x 3 m
Mass of the rectangular sheet (�m): 24 kg
Dimensions of the cut-out square: 1 m x 1 m
Mass of the cut-out square (�1m1): Since the area of the cut-out square is 111/12 of the total area, its mass is 112×24 kg=2 kg(1/12) × 24kg = 2kg.
The original centre of mass of the rectangular sheet (�original,�originalxoriginal,yoriginal): (2 m, 1.5 m), the geometric centre of the sheet.
Since the square is cut from one of the corners, its centre of mass will be at the midpoint of the square. Assuming the bottom left corner of the rectangle as the origin (0,0), the centre of mass of the square is at (0.5 m,0.5 m)(0.5m,0.5m).
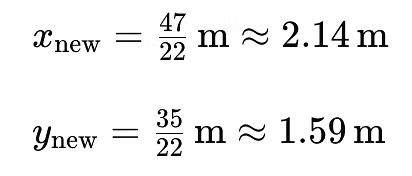
The new centre of mass of the remaining metal sheet, after a square piece is cut out from one of the corners, is approximately
(2.14 m, 1.59 m) from the original bottom left corner.
Motion of Centre of Mass
For a n-particle system of total mass M and individual particles having mass m1, m2, …mn, from the definition of center of mass we can write,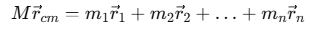
where 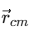 is the position vector of the center of mass, and
is the position vector of the center of mass, and 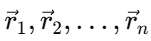 are the position vectors of the individual particles relative to the same origin in a particular reference frame.
are the position vectors of the individual particles relative to the same origin in a particular reference frame.
If the mass of each particle of the system remains constant with time, then, for our system of particles with fixed mass, differentiating the above equation with respect to time, we obtain,
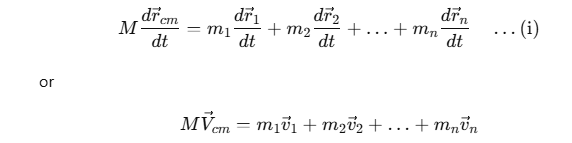
where  are the velocities of the individual particles, and
are the velocities of the individual particles, and 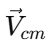 is the velocity of the center of mass. Again differentiating with respect to time, we obtain
is the velocity of the center of mass. Again differentiating with respect to time, we obtain
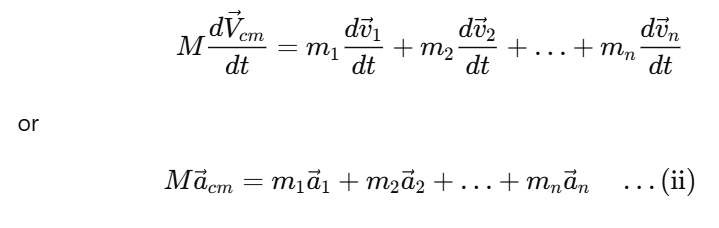
Where 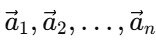 are the accelerations of the individual particles, and
are the accelerations of the individual particles, and 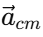 is the acceleration of the center of mass. Now, from Newton’s second law, the force
is the acceleration of the center of mass. Now, from Newton’s second law, the force 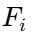 acting on the
acting on the 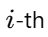 particle is given by
particle is given by 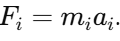 Then, the above equation can be written as
Then, the above equation can be written as
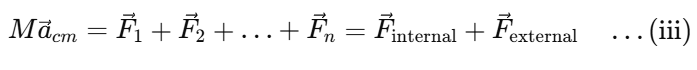
Internal forces are the forces exerted by the particles of the system on each other. However, from Newton’s third law, these internal forces occur in pairs of equal and opposite forces, so their net sum is zero. 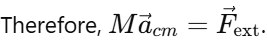
This equation states that the center of mass of a system of particles behaves as if all the mass of the system were concentrated there and the resultant of all the external forces acting on all the particles of the system was applied to it.
Concept: When the parts of a system are rearranged due to internal forces (such as pieces moving away or towards each other, or an internal explosion), and no external force acts on the system, there are two possibilities:
(a) If the system was initially at rest, meaning the centre of mass was at rest, then the centre of mass will remain at rest.
(b) If the system was moving with a constant velocity, the centre of mass will keep moving with the same constant velocity. If the centre of mass had acceleration at the time of the change, like in an explosion, it will continue moving in the same path with the same acceleration as if nothing had happened.
In short, any internal changes in the system do not affect the motion of centre of mass.
Q1. A car of mass 1500 kg is moving east with a speed of 20 m/s, and a truck of mass 3000 kg is moving west with a speed of 10 m/s. Find the velocity of the centre of mass of the system.
Sol: The velocity of the centre of mass is given by:
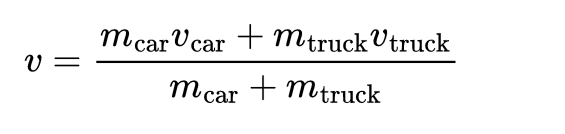
Taking east as positive and west as negative,
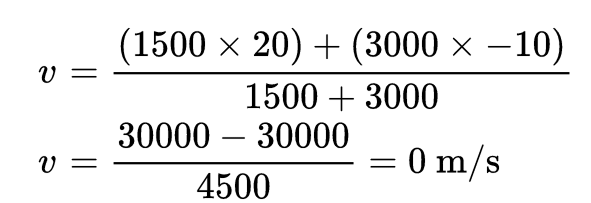
The velocity of centre of mass of the system is 0 m/s, meaning the centre of mass of the system remains stationary.
Q2. Two particles, one of mass 3 kg and the other of mass 2 kg, are moving along the x-axis. If the 3 kg mass has a velocity of 4 m/s to the right and the 2 kg mass has a velocity of 3 m/s to the left, what is the velocity of the centre of mass?
Sol: 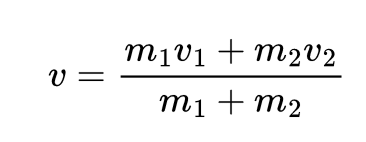
Taking right as positive and left as negative,
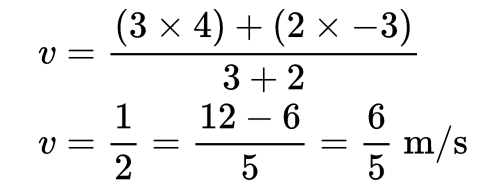
The velocity of centre of mass of the system is 1.2 m/s towards the right.
Q3. A man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform, with what velocity relative to the ice does the platform recoil?
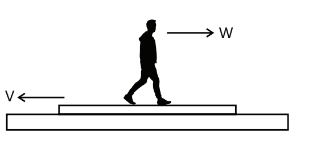


Sure! Please provide the text you would like me to analyze for mistakes.
Applications of Centre of Mass
The centre of mass has various practical applications, including:
- Stability: When constructing buildings or towers, the centre of mass should be lower to ensure stability.
- Motion: In sports and art, performers shift their centre of mass to enhance performance.
- Engineering: Engineers apply the centre of mass concept to create stable and safe structures, such as cranes and bridges.
- Astronomy: The centre of mass is essential in the study of celestial bodies.
magine balancing a pencil on your finger—there’s a special spot where it stays balanced. This is its centre of mass, the point where all of its weight seems concentrated. magine balancing a pencil on your finger—there’s a special spot where it stays balanced. This is its centre of mass, the point where all of its weight seems concentrated.
|
96 videos|367 docs|98 tests
|
FAQs on Centre of Mass - Physics Class 11 - NEET
| 1. What is the definition of the centre of mass in a physical system? |  |
| 2. How do you calculate the centre of mass for a continuous mass distribution? |  |
| 3. What happens to the centre of mass when a part of the mass is removed from the system? |  |
| 4. How does the motion of the centre of mass relate to the motion of individual particles in a system? |  |
| 5. Why is the concept of the centre of mass important in physics and engineering? |  |
















