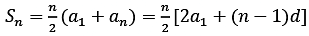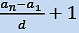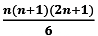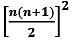UPSC Exam > UPSC Notes > CSAT Preparation > Important Formulae: Progressions
Important Formulas for CAT Progressions
1. Arithmetic Progression Formulae
- an = a1 + (n - 1)d

- Number of terms =

Sum of first n natural numbers
⇒ 1 + 2 + 3 … + n =
Sum of squares of first n natural numbers
⇒ 12 + 22 + 32 + … + n2 =
Sum of cubes of first n natural numbers
⇒ 13 + 23 + 33 ... + n3 =
- Sum of first n odd numbers
⇒ 1 + 3 + 5 … + (2n - 1) = n2 - Sum of first n even numbers
⇒ 2 + 4 + 6 ... 2n = n(n - 1) - If you have to consider 3 terms in an AP, consider {a-d, a, a+d}. If you have to consider 4 terms, consider {a-3d, a-d, a+d, a+3d}
- If all terms of an AP are multiplied with k or divided with k, the resultant series will also be an AP with the common difference dk or d/k respectively.

2. Geometric Progression Formulae
The list of formulas related to GP is given below which will help in solving different types of problems.
- The general form of terms of a GP is a, ar, ar2, ar3, and so on. Here, a is the first term and r is the common ratio.
- The nth term of a GP is Tn = arn-1
- Common ratio = r = Tn/ Tn-1
- The formula to calculate the sum of the first n terms of a GP is given by:
Sn = a[(rn – 1)/(r – 1)] if r ≠ 1and r > 1
Sn = a[(1 – rn)/(1 – r)] if r ≠ 1 and r < 1 - The nth term from the end of the GP with the last term l and common ratio r = l/ [r(n – 1)].
Question for Important Formulae: ProgressionsTry yourself: What is the formula to find the sum of the first n terms of an arithmetic progression?View Solution
- The sum of infinite, i.e. the sum of a GP with infinite terms is S∞= a/(1 – r) such that 0 < r < 1.
- If three quantities are in GP, then the middle one is called the geometric mean of the other two terms.
- If a, b and c are three quantities in GP, then and b is the geometric mean of a and c. This can be written as b2 = ac or b =√ac
- Suppose a and r be the first term and common ratio respectively of a finite GP with n terms. Thus, the kth term from the end of the GP will be = arn-k.

The document Important Formulas for CAT Progressions is a part of the UPSC Course CSAT Preparation.
All you need of UPSC at this link: UPSC
|
218 videos|139 docs|151 tests
|
FAQs on Important Formulas for CAT Progressions
| 1. What is the formula for finding the nth term of an arithmetic progression? |  |
Ans. The formula for finding the nth term of an arithmetic progression is given by: \(a_n = a_1 + (n-1)d\), where \(a_n\) is the nth term, \(a_1\) is the first term, \(n\) is the term number, and \(d\) is the common difference.
| 2. How do you find the sum of the first \(n\) terms of an arithmetic progression? |  |
Ans. The sum of the first \(n\) terms of an arithmetic progression can be calculated using the formula: \(S_n = \frac{n}{2}(2a_1 + (n-1)d)\), where \(S_n\) is the sum of the first \(n\) terms, \(a_1\) is the first term, \(n\) is the number of terms, and \(d\) is the common difference.
| 3. What is the formula for finding the nth term of a geometric progression? |  |
Ans. The formula for finding the nth term of a geometric progression is given by: \(a_n = a_1 \cdot r^{(n-1)}\), where \(a_n\) is the nth term, \(a_1\) is the first term, \(r\) is the common ratio, and \(n\) is the term number.
| 4. How can you calculate the sum of the first \(n\) terms of a geometric progression? |  |
Ans. The sum of the first \(n\) terms of a geometric progression can be found using the formula: \(S_n = \frac{a_1(1-r^n)}{1-r}\), where \(S_n\) is the sum of the first \(n\) terms, \(a_1\) is the first term, \(r\) is the common ratio, and \(n\) is the number of terms.
| 5. What is the difference between an arithmetic progression and a geometric progression? |  |
Ans. In an arithmetic progression, each term is obtained by adding a constant difference to the previous term, while in a geometric progression, each term is obtained by multiplying the previous term by a constant ratio.

|
Explore Courses for UPSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches