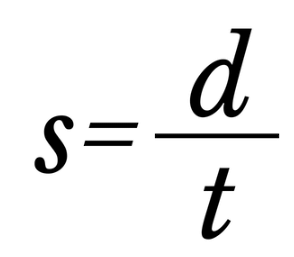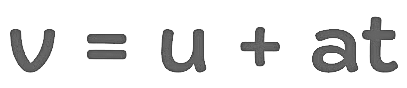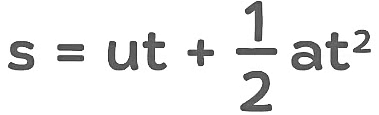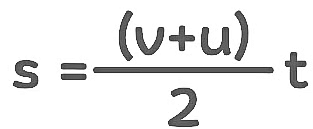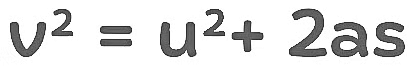Numericals with Answers - Motion | Science Class 9 PDF Download
The study of Class 9 Science Chapter Motion is an essential part of physics, as it helps us understand how objects move and the factors that affect their movement. This chapter covers the basic concepts of motion, including types of motion, distance, displacement, speed, velocity, and acceleration.
Basic Formulae
1. Formula for Speed :
Speed is the distance traveled per unit of time. It is how fast an object is moving.
2. Velocity Formula:
The distance covered by a body in a unit time in a particular direction is called velocity.
Equation of Velocity
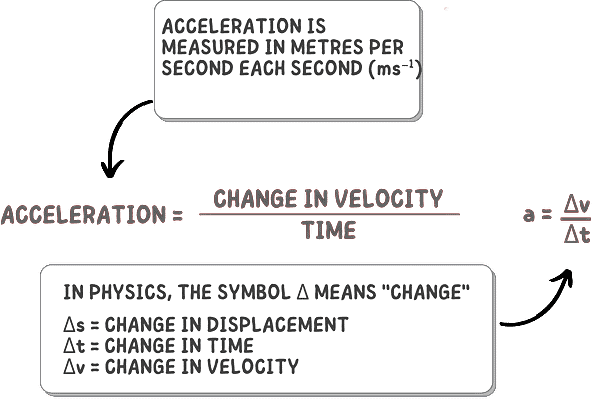
3. Acceleration Velocity Formula:
Acceleration is the rate of change of velocity.
4. Equations of Motion:
The equations of motion of kinematics describe the most fundamental concepts of motion of an object.
(a) The First Equation of Motion
(b) Second Equation of Motion
(c) Third Equation of Motion
5. Squared Velocity Formula
Solved Examples
Q1: A truck travelling at 54 km/h is slow down to 36 km/h in 10 sec. Find the retardation
Ans: Given:
- u=54 km/h =15 m/s
- v=36 km/h=10 m/s
Acceleration is given by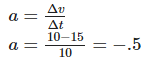
So a=-0.5 m/s2
Negative sign implies retardation
Q2: A train starts from rest and accelerate uniformly at the rate of 5 m/s2 for 5 sec. Calculate the velocity of train in 5 sec.
Ans: Here u=0 ,a= 5m/s2 ,t= 5 sec, To find : v=?
Now using, v=u+at
v=0+5×5
v=25 m/s
Q3: A car start from rest and acquire a velocity of 54 km/h in 2 sec. Find
(i) the acceleration
(ii) distance travelled by car assume motion of car is uniform?
Ans: u=0, v=54 km/h=15 m/s ,t=2 sec
a) Acceleration is given by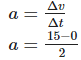
So a=7.5 m/s2
b) Distance is given by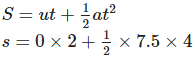
s=15m
Q4: On a 120 km track, a train travels the first 30 km with a uniform speed of 30 km/h. How fast must the train travel the next 90 km so as to average 60 km/h for the entire trip?
Ans: Total distance d = 120 km
Average speed Vav = 60 km/h
Total time = t = ?
Average speed = Total distance/Total time taken
Vav = d/t
t = Putting the values
t = 120/60 = 2h .............(i)
Distance travelled in first part of trip
d1 = 30 km
Speed in first part of the trip v1 = 30 km/h
Time taken in first part of trip
t1 = ?
t1 = putting the values
t1 = 30/30 = 1 h (as time = distance /speed)
Time taken left to complete second part of the trip
t2 = t - t1 = 2 - 1 = 1h
Distance to be covered in second part of the trip
d2 = 90 km
required speed in second part
v2 = ?
Now since, speed = distance/time
v2 = d2/t2 = 90 km/h
Q5: A train accelerates from 36 km/h to 54 km/h in 10 sec.
(i) Acceleration
(ii) The distance travelled by car.
Ans: a. Acceleration is given by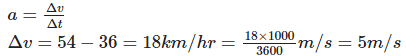
So a= 5/10 m/s2
hence, a=0.5 m/s2
b. Distance is given by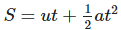
Now u=36 km/hr =10m/s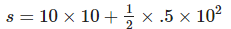
So, s=125m
Q6: A scooter travelling at 10 m/s speed up to 20 m/s in 4 sec. Find the acceleration of scooter.
Ans: Acceleration is given by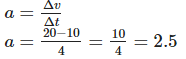
So a=2.5 m/s2
Q7: The maximum speed of a train is 90 km/h. It takes 10 hours to cover a distance of 500 km. Find the ratio of its average speed to maximum speed?
Ans: 
Ratio of average speed to maximum speed= 50:90=5:9
Q8: Two cars A and B race each other. The Car A ran for 2 minute at a speed of 7.5 km/h, slept for 56 minute and again ran for 2 minute at a speed of 7.5 km/h. find the average speed of the car A in the race.
Ans: We know that
Distance=speed×time
Distance travelled in first 2 minute =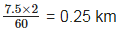
Distance travelled in last 2 minute =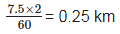
Total distance = .25+.25 = 0.5 km
Total time = 2+2+56 = 60 minute = 1 hr
Average speed = 0.5/1
= 0.5 km/hr
Q9: An object moves along a straight line with an acceleration of 2 m/s2. If its initial speed is 10 m/s, what will be its speed 2 s later?
Ans: Given: u=10 m/s, t=2 s, a=2 m/s2
v=u+at
v=10+2×2
v=14 m/s
Q10: An electron moving with a velocity of 5×103m/s enters into a uniform electric field and acquires a uniform acceleration of 103m/s2 in the direction of initial velocity.
i. Find out the time in which electron velocity will be doubled.?
ii. How much distance electron would cover in this time.?
Ans: Given u=5×103m/s , a=103m/s2, v=2u=104 m/s
i. Using v=u+at
104=5×103+103t
104- 5×103= 103t
or
t=5 sec
ii. Using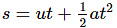
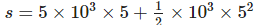
=37.5×103m
Q11: Anand leaves his house at 8.30 A.M for his school. The school is 2 km away and classes start at 9.00 A.M. If he walks at a speed of 3 km/h for the first kilometre, at what speed should he walk the second kilometre to reach just in time?
Ans: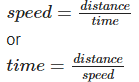
For travelling 1 km with 3 km/hr,
Time taken = 1/3 hr = 20 min
Now he has to reach school in 30 min, So he has cover another 1 km in = 30 -20 =10 min= 1/6 hr
So speed = distance /time
= 1/(1/6)
= 6 km/hr
Q12: A bullet hits a Sand box with a velocity of 20 m/s and penetrates it up to a distance of 6 cm. Find the deceleration of the bullet in the sand box.
Ans: We are given the following information:
Initial velocity, u=20m/s
Distance traveled, d=6cm=0.06m
We can use the equation of motion:
v2=u2+2ad
Since the bullet comes to rest (v=0m/s), we have:
0=u2+2ad
Solving for deceleration (a):
2ad=−u2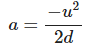
Substituting the given values: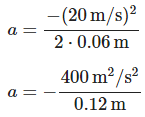
a=−3333.33m/s2 (rounded to two decimal places)
Therefore, the deceleration of the bullet in the sand box is approximately −3333.33m/s2.
Q13: A train 100 m long is moving with the velocity of 72 km/hr. Find the time it takes to cross the bridge which is 2 km long?
Ans: Given Lenght of Train = 100m , velocity = 72 km/hr = 20 m/s, Length of the Bridge =2 Km.
Total distance covered by the train to fully pass the bridge = 2000 + 100 = 2100 m
So, time taken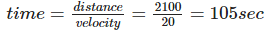
Q14: A bus between Kota to Jaipur passed the 100 km, 160 km and 220 km points at 10.30 am, 11.30 am and 1.30 pm. Find the average speed of the bus during each of the following intervals :
(a) 10.30 am to 11.30 am,
(b) 11.30 am to 1.30 pm and
(c) 10.30 am to 1.30 pm.
Ans: 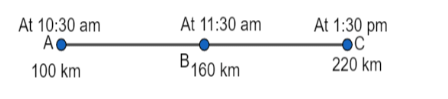 (a) The distance covered between 10.30 am and 11.30 am is 160 km - 100 km = 60 km. The time interval is 1 hour. The average speed during this interval is v1 = 60km/1h = 60 km/h.
(a) The distance covered between 10.30 am and 11.30 am is 160 km - 100 km = 60 km. The time interval is 1 hour. The average speed during this interval is v1 = 60km/1h = 60 km/h.
(b) The distance covered between 11.30 am and 1.30 pm is 220 km -160 = 60 km. The time interval is 2 hours.
The average speed during this interval is v2 = 60km/2h = 30 km/h
(c) The distance covered between 10.30 am and 1.30 pm is 220 km, 100 km = 120 km. The time interval is 3 hours.
The average speed during this interval is, v3 = 120km/3h = 40 km/h.
Q15: The average speed of a bicycle, an athlete and car are 18 km/h, 7 m/s and 2 km/min. respectively. Which of the three is the fastest and which is the slowest?
Ans: 18 km/h = 18km/1h = 18000m/3600s = 5 m/s
2 km/min = 2km/1min = 2000m/60s = 33.3 m/s
Thus the average speeds of the bicycle, the athlete and the car are 5 m/s, 7 m/s and 33.3 m/s respectively. So the car is the fastest and the bicycle is the slowest.
Q16: An object is sliding down on the inclined plane. The velocity changes at a constant rate from 10 cm/s to 15 cm/s in 2 seconds. What is its acceleration?
Ans: 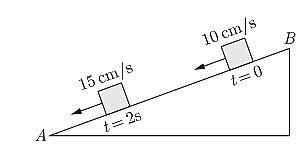 The situation is shown in the figure. Let us take BA as the positive direction. The velocity at t = 0 is u = 10 cm/s and that at t = 25 is v = 15 cm/s.
The situation is shown in the figure. Let us take BA as the positive direction. The velocity at t = 0 is u = 10 cm/s and that at t = 25 is v = 15 cm/s.
Thus, a = 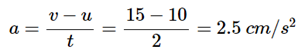
Q17: Figure shows the distance-time graph of two objects A and B which object is moving with greater speed when both are moving?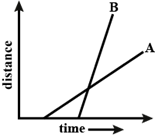 Ans: The line for object B makes a longer angle with the time-axis. Its slope is longer than the slope of the line for object A.
Ans: The line for object B makes a longer angle with the time-axis. Its slope is longer than the slope of the line for object A.
Thus, the speed of B is greater than that of A.
Q18: Figure represents the speed-time graph for a particle. Find the distance covered by the particle between t = 10 min. and t = 30 min.
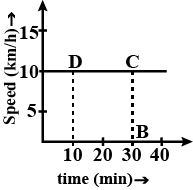
Ans: We draw perpendicular lines from the 10-minute point and the 30-minute point to the time axis (fig.) The distance covered is equal to the area of the rectangle ABCD its value is ABCD = (30 - 10) × (10) = 20 × 10 = (20/60) × 10 = 10/3 km.
Q19: Find the distance covered by a particle during the time interval t = 0 to t = 20 s for which the speed-time graph is shown in the figure.
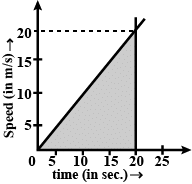
Ans: The distance covered in the time interval 0 to 20 s.
Area of the shaded triangle = 1/2 × base × height. = 1/2 × (20) × (20) = 200 m.
Q20: Figure shows the velocity-time graphs for two objects, A and B, moving along the same direction. Which object has greater acceleration?
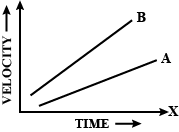
Ans: The slope of the velocity-time graph of B is greater than that for A, Thus, the acceleration of B is greater than that of A.
Q21: A particle moves through a distance of 3 m due east and then 4m due north.
(a) How much is the net distance traversed?
(b) What is the magnitude of the net displacement?
Ans: The situation is shown in the figure. The particle starts from O. It moves through a distance of 3m due east to reach A and then through a distance of 4m due north to reach B.
(a) The total distance moved is 3m + 4m = 7 m,
(b) The magnitude of the net displacement is OB. In the right_angled triangle OAB,
OB2 = OA2 + AB2 = (3m)2 + (4m)2 = 9m2 + 16m2 = 25m2
Therefore, OB = 5 m,
Q22: A car moves 30 km. in 30 min. and the next 30 km. in 40 min. calculate the average speed for the entire journey.
Ans: Given, the total time taken is 30 min + 40 min. = 70 min.
the total distance traversed = 30km + 30 km = 60 km.
The average speed vav = 60km/70min
= 60km/(70/60)h
= 3600/70 km/hr
= 51.4 km/h
Q23: A boy runs for 10 min. at a uniform speed of 9 km/h. At what speed should he run for the next 20 min. So that the average speed comes to 12 km/h?
Ans: Total time = 10 min + 20 min = 30 min.
The average speed is 12 km/h
using s = vt, the distance covered in 30 min = 12 km/h × 30 min = 12km/h x 1/2h = 6km
The distance covered in the first 10 min = 9 km/h × 10 min. = 9km/h x 1/6h = 1.5 km
Thus, he has to cover 6 km - 1.5 km = 4.5 km. in the next 20 min.
The speed required is 4.5km/20min = 4.5km/(20/60)h = 13.5 km/h
Q24: A particle was at rest from 9:00 am to 9:30 am. It moved at a uniform speed of 10 km/h from 9:30 am to 10:00 am. Find the average speed between
(a) 9:00 am and 10:00 am
(b) 9:15 am and 10:00 am
Ans:(a) The distance moved by the particle between 9:30 am and 10:00 am is
s = vt = 10km/h x 1/2h = 5 km.
This is also the distance moved between 9:00 am and 10:00 am. Thus, the average speed during this interval is
vav = s/t = 5km/1h = 5 km/h
(b) The distance moved between 9:30 am and 10:00 am is 5km. This is also the distance moved in the interval 9:15 am to 10:00 am. The average speed during this interval is _
vav = s/t = 5km / 45min = 6.67 km/h.
Q25: It is estimated that the radio signal takes 1.27 seconds to reach the earth from the surface of the moon. Calculate the distance of the moon from the earth. Speed of radio signal = 3 × 108 ms-1 (speed of light in air).
Ans: Here, time = 1.27 s
speed = 3 × 108 ms-1
distance = ?
Using distance = speed × time, we get
distance = 3 × 108 × 1.27
= 3.81 × 108 km
= 3.81 × 105 km
Q26: A wireless signal is sent to earth from a spacecraft. This signal reaches the earth in 300 seconds. Calculate the distance of the spacecraft from the earth. Given, speed of the signal = 3 × 108 ms-1.
Ans: Here, t = 300 s
Speed, v = 3 × 108 ms-1
Distance = ?
Using distance = speed × time, we get
distance = 3 × 108 × 300 = 9 × 1010 m = 9 = 107 km
Thus, distance of spacecraft from earth = 9 × 107 km.
Q27: A sound is heard 5 seconds later than the lightning is seen in the sky on a rainy day. Find the distance of the location of lightning. Given speed of sound = 346 ms-1.
Ans: Here, t = 5 s
Speed, v = 346 ms-1
Distance = ?
Using distance = speed × time, we get
distance = 346 ms-1 × 5 s = 1730 m
Thus, distance of the location of lightning = 1730 m
Q28: A particle is moving in a circle of diameter 20 m. What is its distance and as per the table given below
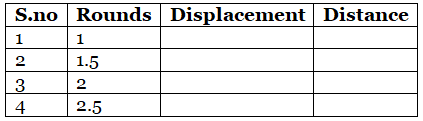
Ans: After every round, particle comes to it starting position. So displacement at full rounds will be zero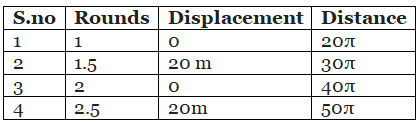
Q29: An object dropped from a cliff falls with a constant acceleration of 10 m/s2. Find its speed 5 s after it was dropped.
Ans: v = u + at
u = 0
v = 10 x 5
v = 50m/s
Q30: A ball is thrown upwards and it goes to the height 100 m and comes down
(i) What is the net displacement?
(ii) What is the net distance?
Ans: As it comes down to the initial point
(i) Net displacement is zero
(ii) Net distance=200 m
Go through detailed chapter notes of this chapter here.
You can find NCERT Solution of the chapter here.
|
84 videos|544 docs|60 tests
|
FAQs on Numericals with Answers - Motion - Science Class 9
| 1. What is the formula for calculating speed in motion? |  |
| 2. How do you calculate distance using time and speed? |  |
| 3. What is the difference between speed and velocity? |  |
| 4. Can you explain what uniform motion is? |  |
| 5. What are some examples of practical applications of motion formulas? |  |