Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
Q1: If the difference between the circumference and the radius of a circle is 37 cm, then using π = 22/7, calculate the circumference (in cm) of the circle.
Sol: 2πr – r = 37 ⇒ r(2π – 1) = 37
⇒ r ( 447 − 1) = 37 ⇒ r ( 377 )= 37
⇒ r = 37 × 737 = 7 cm
Circumference of the circle = 2πr = 2 × 227 × 7 = 44 cm
Q2: If he is taken as 22/7, calculate the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution.
Sol: Radius (r) = 35/2
Required distance = Perimeter = 2πr
= 2 × 22/7 × 35/7 cm = 110 cm or 1.1 m
Q3: In the Figure, PQ and AB are respectively the arcs of two concentric circles of a radii 7 cm and 3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [Use π = 22/7]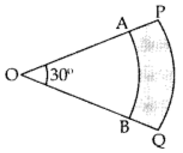 Sol: Area of sector with radius 7 cm
Sol: Area of sector with radius 7 cm
π × 7 × 7 × 30360 = 49π12
Area of sector with radius 3.5 cm:
π × 72 × 72 × 30360 = 49π48
∴ Area of the shaded region:
49π12 − 49π48 = 196π − 49π48
= 147π48 = 14748 × 227 = 778
= 9.625 sq. cm
Q4: Find the area of the major segment APB, in the figure of a circle of radius 35 cm and ∠AOB = 90°. (Use π = 22/7)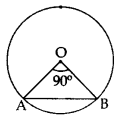 Sol: Here θ = 90°, p = OA = OB = 35 cm
Sol: Here θ = 90°, p = OA = OB = 35 cm
Area of minor segment = ar(minor sector) – ar(∆AOB)
θ360° πr2 − 12 × OA × OB
= 90°360° × 227 × 352 − 12 × 35 × 35
= 35 × 35 11 − 714
= 35 × 35 × 414 = 350 cm2
Area of circle = πr2:
= 227 × 35 × 35 = 3,850 cm2
Area of shaded region (major segment):
= Area of circle − Area of minor segment
= 3,850 − 350 = 3,500 cm2
Q5: A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. (Use π = 22/7 and √3 = 1.73)
Sol: Here θ = 120°, r = 14 cm
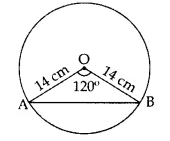 Area of shaded region (minor segment):
Area of shaded region (minor segment):
= ar(minor sector) − ar(ΔAOB)
= θ360° πr2 − r2 sin θ2 cos θ2
= 120°360° × 227 × (14)2 − (14)2 × sin 120°2 × cos 120°2
= (14)2 2221 − sin 60° cos 60°
= 14 × 14 2221 − √32 × 12
= 14 × 14 88 − 21√384
= 146 × [88 − 21(1.73)]
= 73 × [88 − 36.33]
= 73 × 51.67 = 120.56 cm2
Q6: In Figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)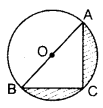 Sol: ∠ACB = 90° …[Angle in a semi-circle
Sol: ∠ACB = 90° …[Angle in a semi-circle
∴ AC2 + BC2 = AB2 …[Pythagoras’ theorem
(12)2 + BC2 = (13)2
144 + BC2 = 169
BC2 = 169 – 144 = 25
BC = + 5 cm
Radius, r = OA = OB = AB2 = 132 cm
Area of shaded region:
= Area (semi-circle) − Area (ΔACB)
= 12 πr2 − 12 × base × corresponding altitude
= 12 × 3.14 × ( 1322 )− 12 × 5 × 12
= 3.14 × 1698 − 30
= 66.33 − 30
= 36.33 cm2
Q7: In Figure, ABC is a right-angled triangle right angled at A. Semicircles are drawn on AB, AC and BC as diametres. Find the area of the shaded region.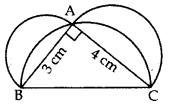 Sol: In rt. ∆BAC,
Sol: In rt. ∆BAC,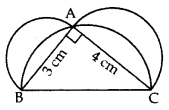
∴ BC2 = AB2 + AC2 …[Pythagoras’ theorem
= (3)2 + (4)
= 9 + 16 = 25 cm2
∴ BC = +5 cm … [Side of ∆ can’t be -ve
Area of the shaded region:
= [area of semi-circle whose diagonal is AB] + [area of semi-circle whose diagonal is AC]
− [area of semi-circle whose diagonal is BC] + ar(ΔABC)
= 12 πr12 + 12 πr22 − 12 πr32 + 12 × AB × AC
Where:
ar(semi-circle) = 12 πr2
ar(Δ) = 12 × base × corresponding altitude
r1 = AB2 = 32 cm
r2 = AC2 = 42 cm
r3 = BC2 = 52 cm
Substituting values:
= 12 π(r12 + r22 − r32) + 12 × 3 × 4
= 12 × 227 × [ 322 + 422 − 522 ] + 6
= 117 × [ 94 + 164 − 254 ] + 6
= 117 × 0 + 6 = 6 cm2
Q8: In the given figure, OAPB is a sector of a circle of radius 3.5 cm with the centre at O and ∠AOB = 120°. Find the length of OAPBO.

Sol: Here, the major sector angle is given by θ = 360° − 120° = 240°
Radius = 3.5 cm = 3510 cm = 72 cm
∴ Circumference of the sector APB:
= θ360 × 2πr = 240360 × 2 × 227 × 72 cm
= 23 × 22 cm = 443 cm
∴ Perimeter of OAPBO = [Circumference of sector AOB] + OA + OB
= 443 + 72 + 72 = 443 + 7
= 443 + 213 = 653 or 21 23 cm
Q9: Find the area of a square inscribed in a circle of radius 10 cm.
Sol: Let ABCD be the square such that

AB = BC = 10 cm
∴ AC2 = AB2 + BC2
AB2 + BC2 = (10 × 2)
⇒ x2 + x2 = (20)2
[Let AB = BC = x]
⇒ 2x2 = 400
⇒ x2 = 4002 = 200 cm2
∴ Area of the square = 200 cm2.
Q10: In the given figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter of the shaded region.

Sol. O is the centre of the circle.
∴ AB is its diameter.
In right Δ ABC,
AC2 + BC2 = AB2
⇒ 122 + 162 = AB2
⇒ 144 + 256 = AB2 ⇒ AB2 = 400
⇒ AB = √400 = 20 cm
∴ Circumference of semi-circle ACB:
= 12 (2πr)
= 12 × 2 × 227 × 202 cm
= 11 × 207 cm = 2207 cm
∴ Perimeter of the shaded region = 22/7 cm + 12 cm + 16 cm
= 31.43 cm + 12cm + 16cm
= 59.43 cm
|
127 videos|550 docs|75 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Area Related to Circles
| 1. What is the formula for calculating the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How can I calculate the area of a circle if I only have the diameter? |  |
| 5. What units are used when measuring the area of a circle? |  |























