Previous Year Questions: Triangles | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Previous Year Questions 2024 |

|
| Previous Year Questions 2023 |

|
| Previous Year Questions 2022 |

|
| Previous Year Questions 2021 |

|
| Previous Year Questions 2020 |

|
| Previous Year Questions 2019 |

|
Previous Year Questions 2024
Q1: In ΔABC, DE || BC (as shown in the figure). If AD = 2 cm, BD = 3 cm, BC = 7.5 cm, then the length of DE (in cm) is: (CBSE 2024) (a) 2.5
(a) 2.5
(b) 3
(c) 5
(d) 6
 View Answer
View Answer 
Ans: (b) 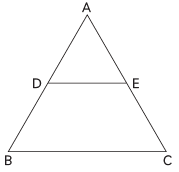
Consider the triangles ΔADE and ΔABC.
Since DE || BC, the corresponding angles are equal.
Hence,
∠ADE = ∠ABC
∠AED = ∠ACB
Thus, by AA similarity, we find that ΔADE and ΔABC are similar.
So, ΔADE ~ ΔABC.
When two triangles are similar, their corresponding sides are proportional.
This gives the equation:
AE/AC = DE/BC = AD/AB
From this, we write:
AD/AB = DE/BC
We know that:
AB = AD + BD = 2 + 3 = 5 cm
Substituting values:
2/5 = DE/7.5
Using cross multiplication:
2 × 7.5 = 5 × DE
DE = (15/5)
DE = 3 cm
Q2: In ΔABC, if AD ⊥ BC and AD2 = BD × DC, then prove that ∠BAC = 90º. (CBSE 2024)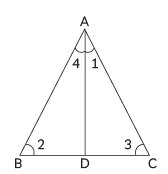
 View Answer
View Answer 
Ans: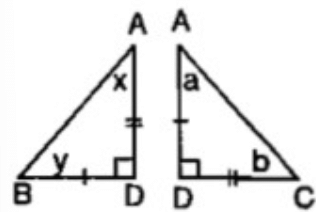

Q3: The greater of two supplementary angles exceeds the smaller by 18°. Find the measures of these two angles. (2024)
 View Answer
View Answer 
Ans:
Let the measures of the two angles be x° and y° (x > y).
Given:
x + y = 180° ........ (i) (Sum of Supplementary angles are 180°)
Also,
x - y = 18° ........ (ii) (Given)
Adding both the equations, we get:
2x = 198°
x = 99°
By putting value of x in equation (i)
we get,
99° + y = 180°
y = 180° - 99° = 81°
Hence, y = 81° and x = 99°.
Q4: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio. (2024)
 View Answer
View Answer 
Ans:
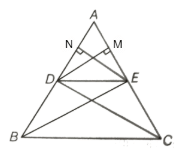 Given: In ΔABC, DE || BC
Given: In ΔABC, DE || BC
To Prove: DB/AD =EC/AE
Proof:
In ΔABC and ΔADE
∠AED = ∠ACB (Corresponding angles)
∠ADE = ∠ABC (Corresponding angles)
∠EAD is common to both the triangles
∴ ΔAED ~ ΔACB by AAA similarity
⇒ AC / AE = AB / AD ( ∴ corresponding sides of similar triangles are proportional) ...............(i)
⇒ Also, AC = AE + EC and AB = AD + BD
Putting these values in (i), we get
⇒ (AE + EC) / AE = (AD + BD) / AD
⇒ EC / AE = BD / AD
Hence proved.
Q5: Sides AB and BC and median AD of a ΔABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC ∼ ΔPQR. (2024)
 View Answer
View Answer 
Ans: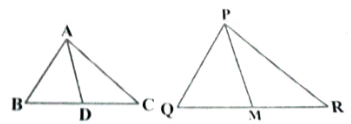
Since AD and PM are medians of ΔABC and ΔPQR,
∴ BD = 1/2 BC and QM = 1/2 QR ……….(1)
Given that,
AB / PQ = BC / QR = AD / PM ……….(2)
From (1) and (2),
AB / PQ = BD / QM = AD / PM ……….(3)
In ΔABD and ΔPQM,
AB / PQ = BD / QM
By SSS criterion of proportionality,
ΔABD ~ ΔPQM
∴ ∠B = ∠Q (Corresponding Sides of Similar Triangles) ……….(4)
In ΔABC and ΔPQR,
AB / PQ = BC / QR (From 2)
∠B = ∠Q (From 4)
By SAS criterion of proportionality,
ΔABC ~ ΔPQR
Q6: In the given figure, ABCD is a quadrilateral. Diagonal BD bisects ∠B and ∠D both. (2024)
Prove that:
(i) ΔABD ∼ ΔCBD
(ii) AB = BC

 View Answer
View Answer 
Ans: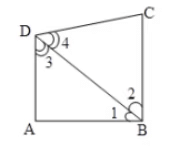
i. Given: diagonal BD bisects ∠B and ∠D
To prove: ΔABD ~ ΔCBD
Proof: In ΔABD and ΔCBD
∠ABD = ∠CBD … (BD bisects ∠B)
∠ADB = ∠CDB … (BD bisects ∠D)
Therefore, ΔABD ~ ΔCBD … (by AA rule)
Hence proved
ii. Since, ΔABD ~ ΔCBD
Therefore, ABBD = BCBD … (by cpst)
Hence, AB = BC
Hence proved.
Q7: In the given figure, PA, QB, and RC are each perpendicular to AC. If AP = x, BQ = y, and CR = z, then prove that (1/x) + (1/z) = (1/y). (CBSE 2024)
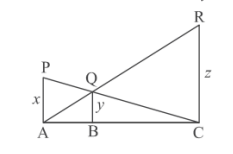
 View Answer
View Answer 
Ans:
In ΔCAP and ΔCBQ
∠CAP = ∠CBQ = 90°
∠PCA = ∠QCB (common angle)
So, ΔCAP ~ ΔCBQ ... (By AA similarity Rule)
Hence, BQAP = BCAC ⇒ yx = BCAC ... (i) (Corresponding part of similar triangle)
Now, in ΔACR and ΔABQ
∠ACR = ∠ABQ = 90°
∠QAB = ∠RAC (common angle)
So, ΔACR ~ ΔABQ (By AA similarity Rule)
Hence, BQCR = ABAC ⇒ yz = ABAC ... (ii) (Corresponding part of similar triangle)
On adding eq. (i) and (ii), we get
yx + yz = BCAC + ABAC
⇒ y(1/x + 1/z) = BC + ABAC
⇒ y(1/x + 1/z) = 1
1/x + 1/z = 1/y
Hence proved.
Previous Year Questions 2023
Q8: In ΔABC, PQ || BC If PB = 6 cm, AP = 4 cm, AQ = 8 cm. find the length of AC. (2023)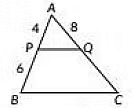 (a ) 12 cm
(a ) 12 cm (b) 20 cm
(c) 6 cm
(d) 14 cm
 View Answer
View Answer 
Ans: (b)
Sol: Since, PQ || BC
∴ APPB = AQQC .......... (By Proportionality Theorem)
⇒ 46 = 8QC
⇒ QC4 = 8 × 64
= 12 cm
Now length of AC = AQ+QC = 12+8 = 20 cm
Q9: In the given figure, XZ is parallel to BC. AZ = 3 cm, ZC = 2 cm, BM = 3 cm and MC = 5 cm. Find the length of XY. (2023)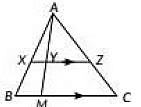
 View Answer
View Answer 
Ans:
Given: AZ = 3 cm, ZC = 2 cm, BM = 3 cm, and MC = 5 cm.
Proof:
We can calculate the lengths of AC and BC:
- AC = AZ + ZC = 3 + 2 = 5 cm,
- BC = BM + MC = 3 + 5 = 8 cm.
Next, in triangles AXY and ABM, we know that:
- ∠AXY = ∠ABM (corresponding angles since XZ is parallel to BC),
- ∠XAY = ∠BAM (common angle).
∴ By the AA similarity criterion (Angle-Angle similarity):
ΔAXY ~ ΔABM.
Since these triangles are similar, their corresponding sides are proportional:
AX / AB = XY / BM = AZ / AC.
From the proportionality, we substitute the known values:
AX / AB = AZ / AC, which simplifies to:
XY / BM = AZ / AC.
Substituting the known values of AZ = 3 cm and AC = 5 cm, we get:
XY / 3 = 3 / 5.
Now, solving for XY, we multiply both sides by 3:
XY = (3 × 3) / 5 = 9 / 5 = 1.8 cm.
Thus, the length of XY is 1.8 cm.
Q10: Assertion (A): The perimeter of ΔABC is a rational number.
Reason (R): The sum of the squares of two rational numbers is always rational. (2023)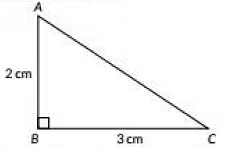
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
 View Answer
View Answer 
Ans: (d)
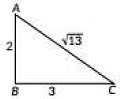
In ΔABC, AC2 = AB2 + BC2 (Using Pythagoras Theorem)
⇒ AC2 = 22 + 32
⇒ AC2 = 4 + 9
⇒ AC= √13 cm
So, perimeter is (2 + 3 + √13)cm = (5 + √13), which is irrational.
Hence, Assertion in false but Reason is true.
Q11: In a ΔPQR, N is a point on PR, such that QN ⊥ PR. If PN × NR = QN2, prove that ∠PQR = 90°. (CBSE 2023)
 View Answer
View Answer 
Ans: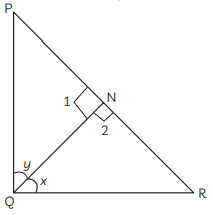
We have, PN . NR = QN²
∴ PN / QN = QN / NR …(i)
In ΔQNP and ΔRNQ,
PN / QN = QN / NR (from (i))
And ∠PNQ = ∠RNQ (Each equal to 90°)
∴ ΔQNP ~ ΔRNQ [By SAS similarity criterion]
Then, ΔQNP and ΔRNQ are equiangular,
i.e., ∠PQN = ∠QRN
⇒ ∠QRN = ∠QPN
On adding both sides, we get:
∠PQN + ∠QRN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN …(ii)
We know that the sum of angles of a triangle is 180°.
In ΔPQR,
∠PQR + ∠PQR + ∠QR = 180°
⇒ ∠PQR + ∠QRN + ∠QRN = 180° [∴ ∠PQR = ∠QPN and ∠QRN = ∠QRN]
⇒ 2∠PQR = 180° [Using equation (ii)]
⇒ ∠PQR = 180° / 2 = 90°
∴ ∠PQR = 90°
Hence proved.
Q12: In the given figure, ΔABC and ΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)= AODO. (CBSE 2023)
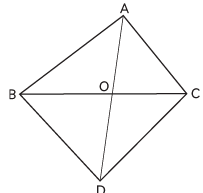
 View Answer
View Answer 
Ans: Given: ΔABC and ΔDBC are on the same base BC. AD and BC intersect at O.
To Prove:
ar(ΔABC)ar(ΔDBC)= AODO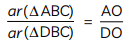
Construction: Draw AL ⊥ BC and DM ⊥ BC
Proof:
Now, in ΔALO and ΔDMO, we have
∠ALO = ∠DMO = 90°
∠AOL = ∠DOM (Vertically opposite angles)
Therefore, ΔALO ~ ΔDMO (By AA criterion)
∴ ALDM = AODO (Corresponding sides of similar triangles are proportional)
ar(ΔABC)ar(ΔDBC) = 1/2 × BC × AL1/2 × BC × DM
⇒ ALDM = AODO
Hence, proved.
Q13: In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm, and BQ = 5 cm, then the length of BC is ______.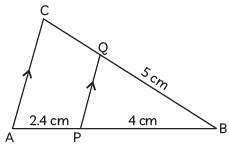
(a) 8 cm
(b) 3 cm
(c) 0.3 cm
(d) 25/3 cm (CBSE 2023)
 View Answer
View Answer 
Ans: (a)
As PQ || AC by using basic proportionality theorem
⇒ BPPA = BQQC
⇒ 42.4 = 5QC
⇒ QC = 5 × 2.44
⇒ QC = 5 × 0.6
QC = 3 cm
∴ BC = BQ + QC
= 5 + 3
= 8 cm
Previous Year Questions 2022
Q14: In the figure given below, what value of x will make PQ || AB? (2022)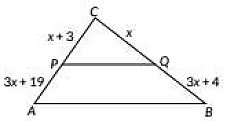 (a) 2
(a) 2
(b) 3
(c) 4
(d) 5
 View Answer
View Answer 
Ans: (a)
Sol: Suppose PQ || AB
By using Proportionality theorem we have
CPPA = CQQB
⇒ x + 33x + 19 = x3x + 4
⇒ 3x² + 19x = 3x² + 9x + 4x + 12
⇒ 6x = 12
⇒ x = 2
Q15: If Δ ABC and Δ PQR are similar triangles such that ∠A = 31° and ∠R = 69°, then ∠Q is : (2022)
(a) 70°
(b) 100°
(c) 90°
(d) 80°
 View Answer
View Answer 
Ans: (d)
Sol: Given Δ ABC and Δ PQR are similar.
Hence, ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R
We know that,
∠P + ∠Q + ∠R = 180°
31° + ∠Q + 69° = 180°
100° + ∠Q = 180°
∠Q = 180° - 100°
∠Q = 80°
Q16: A vertical pole of length 19 m casts a shadow 57 m long on the ground and at the same time a tower casts a shadow 51m long. The height of the tower is (2022)
(a) 171m
(b) 13 m
(c) 17 m
(d) 117 m
 View Answer
View Answer 
Ans: (c)
Sol: Let AB be the pole and PQ be the tower
Let height of tower be h m
Now, ΔABC ∼ ΔPQR
∴ ABPQ = BCQR
⇒ 19h = 5751
⇒ h = 19 x 5157
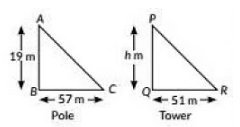
⇒ h = 17m
Previous Year Questions 2021
Q17: Aman goes 5 metres due west and then 12 metres due North. How far is he from the starting point? (2021) View Answer
View Answer 
Ans: 13 m
Let Aman starts from A point and continues 5 m towards west and readied at B point, from which he goes 12 m towards North reached at C point finally.
In ΔABC, we have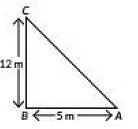
AC2 = AB2 + BC2 ............ [By Pythagoras theorem]
AC2 = 52 + 122
AC2 = 25 + 144 = 169
AC = 13m
So, Aman is 13 m away from his starting point.
Previous Year Questions 2020
Q18: All concentric circles are ___________ to each other. (2020) View Answer
View Answer 
Ans: All concentric circles are similar to each other.
Q19: In figure, PQ || BC, PQ = 3 cm, BC = 9 cm and AC = 7.5 cm. Find the length of AQ. (2020)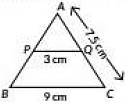
 View Answer
View Answer 
Ans: Given, PQIIBC
PQ = 3 cm, BC = 9 cm and AC = 7.5 cm
Since. PQ || BC
∴ ∠APQ = ∠ABC (Corresponding angles are equal)
Now, in ΔAPQ and ΔABC
∠APQ =∠ABC (Corresponding angles are equal)
∠A = ∠A (Common)
ΔAPQ ∼ ΔABC (AA similarity)
∴ APAB = AQAC = PQBC
⇒ AQAC = 39
⇒ AQ7.5 = 13
⇒ AQ = 7.53 = 2.5 cm
Q20: In the given figure, EA/EC = EB/ED, prove that ΔEAB ~ ΔECD. (CBSE 2020)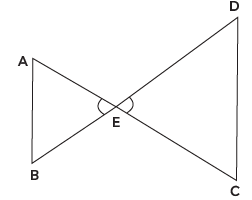
 View Answer
View Answer 
Ans: In ΔEAB and ΔECD
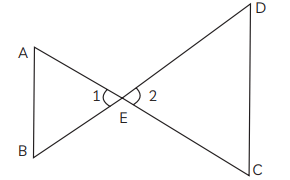
Acc to Converse of basic proportionality theorem, It states that if any line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
It is given that
Since, EA/EC = EB/ED
∠1 = ∠2 [Vertically opposite angles]
So, by SAS similarity criterion ΔEAB ~ ΔECD
Hence, proved.
Previous Year Questions 2019
Q21: In the figure, GC||BD and GE||BF. If AC = 3cm and CD = 7 cm, then find the value of AE / AF. (2019)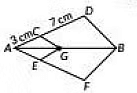
 View Answer
View Answer 
Ans: 3/10
Here in the given figure.
GC || BD and GE || BF
AC = 3 cm and CD = 7 cm
By Basic Proportionality theorem.
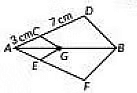
We get, ACCD = AEEF
∴ AE / EF = 3 / 7
⇒ AF / AE = 7 / 3
⇒ AE + EF / AE = 3 + 7 / 3
⇒ AF / AE = 10 / 3
Thus, AE / AF = 3 / 10.
Q22: The perpendicular from A on the side BC of a ΔABC intersects BC at D, such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2. (2019)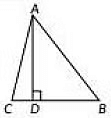
 View Answer
View Answer 
Ans:
In ΔABC, AD ⟂ BC and BD = 3CD
BD + CD = BC
3CD + CD = BC
4CD = BC
CD = (1/4) BC …… (1)
and, BD = (3/4) BC …… (2)
In ΔADC, ∠ADC = 90°
AC² = AD² + CD² [Using Pythagoras theorem]
AD² = AC² - CD² ….. (3)
In ΔADB, ∠ADB = 90°
AB² = AD² + BD² [Using Pythagoras theorem]
AB² = AC² - CD² + BD² [from equation (3)]
AB² = AC² + (3/4 BC)² - (1/4 BC)² [from equations (1) and (2)]
AB² = AC² + (9BC² - BC²)/16
AB² = AC² + 8BC²/16
AB² = AC² + 1/2 BC²
Thus, 2AB² = 2AC² + BC²
|
127 videos|584 docs|79 tests
|
FAQs on Previous Year Questions: Triangles - Mathematics (Maths) Class 10
| 1. What are the different types of triangles based on their sides and angles? |  |
| 2. How do you calculate the area of a triangle? |  |
| 3. What is the Pythagorean theorem and how does it relate to right triangles? |  |
| 4. How can you determine if a triangle is congruent to another triangle? |  |
| 5. What are the properties of the angles in a triangle? |  |
















