Class 10 Maths Chapter 6 HOTS Questions - Triangles
Q1: A quadrilateral OABC in which OA = OC. The bisector of ∠AOB meet AC at D and AB at F and the bisector of ∠COB meets AC at E and BC at G. Prove that ∆ODE ~ ∆OFG.
Ans: We know that bisector of an angle of a triangle divides the opposite side in the ratio of sides containing the angle.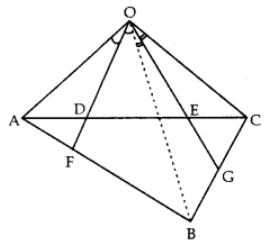

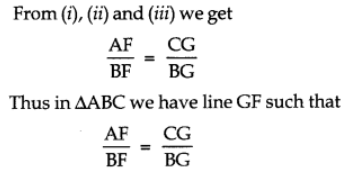
⇒ FG || DE …(iv)
[by converse of Basic Proportionality Theorem]
In ∆ODE and ∆OFG, we have
⇒ AODE ~ AOFG [SAS similarity]
Hence proved.
Q2: Bisector of ∠B and ∠C in ∆ABC meet each other at X. Line AX cuts the side BC in Y. Prove that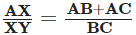
Ans: In ∆ABY, BX is bisector of ∠B.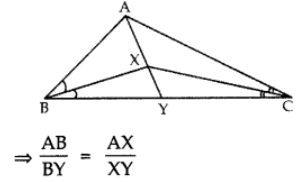
[Bisector of an angle of a triangle divides the opp. sides in the ratio of sides containing the angles.] ….. (i)
Similarly, in ∆ACY, CX is bisector of ∠C.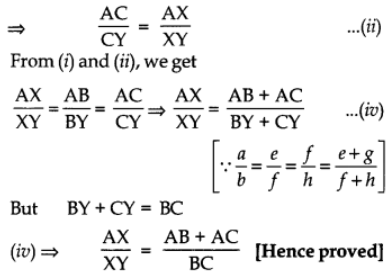
Q3: CE and DE are equal chords of a circle with centre O. If ∠AOB = 90°, then find ar(∆CED): ar(∆AOB). Ans:
Ans:
In ∆CED, we have ∠CED = 90°
[∵ Angle in semicircle is a right angle]
∠1 = ∠2 = 45°
[∵ CE = DE (given) and ∠1 + ∠2 = 90°]
In ∆AOB, ∠AOB = 90° [given]
⇒ OA = OB [Radii of same circle]
⇒ ∠3 = ∠4 = 45°
Now in ∆CED and ∆AOB
∠CED = ∠AOB [each 90°]
∴ ∠1 = ∠3 [each 45°]
∴ ∠2 = ∠4 [each 45°]
∆CED ~ ∆AOB [AAA similarity]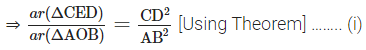
Now CD = 2OD = 2OB
⇒ CD2 = 4(OB2)
In right ∆AOB
AB2 = OA2 + OB2 = OB2 + OB2 = 2(OB)2
[∵ OA = OB (Radii of same circle)]
From (i) and (ii), we get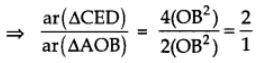
Thus, ar (∆CED): ar (∆AOB) = 2:1
Q4: The internal bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.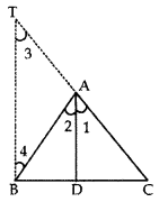
Ans: Given: A ∆ ABC such that ,X bisector of ∠A meets BC in D.
To prove: 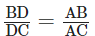 Construction: BT parallel to AD, meeting CA produced at point T.Proof: Now BT || AD and CT is a transversal.
Construction: BT parallel to AD, meeting CA produced at point T.Proof: Now BT || AD and CT is a transversal.
⇒ ∠1 = ∠3 ……. (i)
[Corresponding angles]
Further BT || AD and AB is a transversal.
⇒ ∠2 = ∠4 [Alternate angles] ……. (ii)
But ∠1 = ∠2 ……. (iii)
[Given as AD is bisector of ∠BAC]
From (i), (ii) and (iii), we get
∠3= ∠4
⇒ AB = AT …(to)
[∵ Sides opposite to equal angles are also equal]
Also in ABCT, DA || BT
∴ By B.P.T.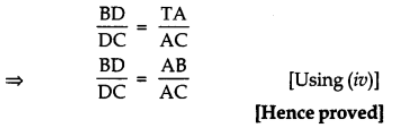
|
127 videos|584 docs|79 tests
|
















