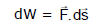Introduction to Work and Work Energy Theorem | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Introduction |

|
| What is Work in Physics? |

|
| Work Done by a Constant Force |

|
| Work Done by a Variable Force |

|
| Work Done by Area Under F-S or F -x Graph |

|
| Work Energy Theorem |

|
Introduction
In common language, the term "work" often brings to mind images of physical labor, like lifting heavy objects or doing chores. However, in science, "work" has a very specific meaning that differs from our everyday understanding.
This document aims to clarify the scientific definition of work and how it differs from the physiological pictures we might have in mind.
What is Work in Physics?
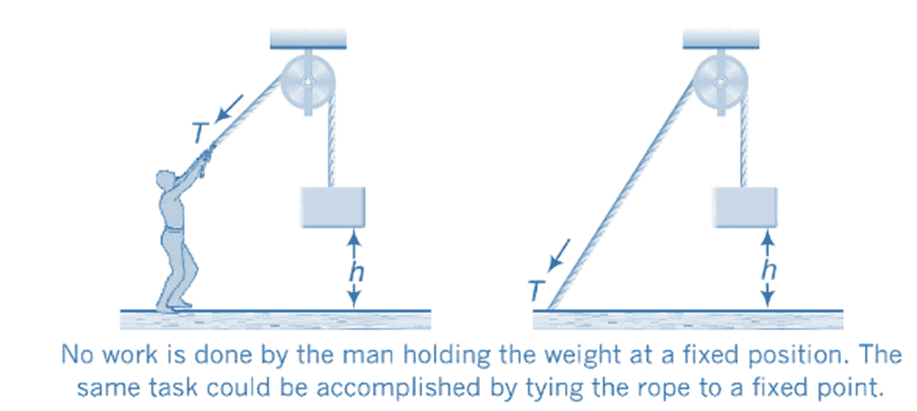
- Consider the scenario of a person holding a weight at a height 'h' above the floor, as depicted in the figure.

- In everyday language, we might say that the person is doing work, but according to our scientific definition, no work is performed by a force acting on an object at rest, possibly because the force applied by the person was not sufficient enough to produce any movement in the weight he was holding.
- In physics, a force is said to work only when it acts on a body, and if there is a consequential displacement of the point of application in the direction of the force.

- There are mainly two methods of finding work done by a force:

Work Done by a Constant Force
Say, if a constant force F displaces a body through displacement s then the work done, W, is given by
W = F d cosθ = F.d,
where,
d is the magnitude of displacement and
θ is the angle between force and displacement.
The SI unit of work is Joule or Newton-metre.
- In the image above, the force F has been broken into rectangular components: F sinθ and Fcosθ.
- The component, Fsinθ does not work as the body does not move up or down. All the work is done by the component, Fcosθ.
- Hence, work done by a force is the product of a component of force in the direction of displacement and magnitude of displacement.
- The component of force perpendicular to the object's displacement does zero work.
Unit of Work
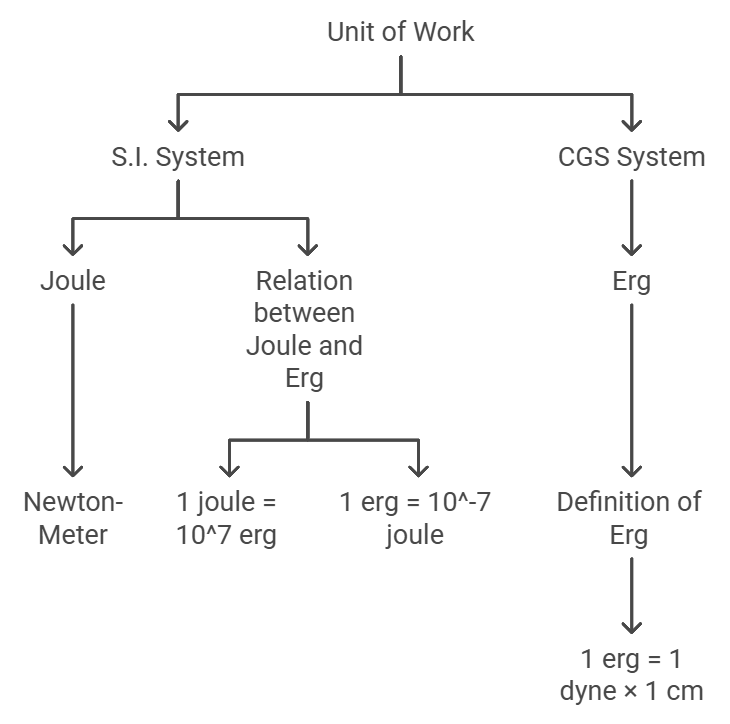
In the S.I. system, the unit of work done is Joule. Another name for joule is newton-meter.In the CGS system, the unit of work is erg.
One erg of work is said to be done when a force of one dyne displaces a body through one centimeter in its direction.
1 erg = 1 dyne × 1 cm = 1 g cm s-2 × 1 cm = 1 g cm2 s-2
Relation between joule and erg:
1 joule = 1 newton × 1 metre
1 joule = 105 dyne × 102 cm = 107 dyne cm
1 joule = 107 erg
1 erg = 10-7 joule
Dimensions of Work
[Work] = [Force] [Distance] = [MLT-2] [L] = [ML2T-2]
Nature of Work
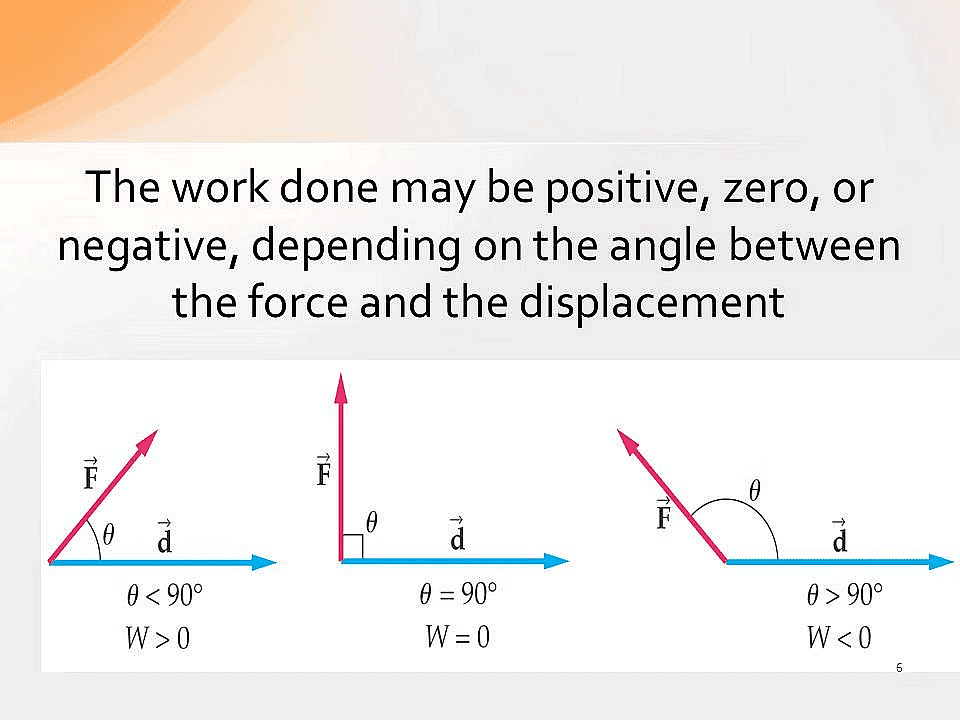
Looking at this equation W = F d cosθ, we can understand three different scenarios for the work done:
 Nature of Work
Nature of Work
1. Positive Work:
When the force and the direction of movement are at an acute angle (θ < 900), cosθ is positive. Hence, the work done is positive.
For example, when a body falls freely under the force of gravity, θ=00, cosθ=+1, so the work done by gravity is positive; when a horse pulls a cart on a flat road; when a spring is stretched, in such cases, the work done is positive.
 For a body freely falling under gravity work done by gravity is positive
For a body freely falling under gravity work done by gravity is positive
2. Zero Work:
If the force applied and the direction of movement are at right angles (perpendicular), i.e. θ=900, cosθ=0, the work done is zero.
For example, when an object is moved in a circular path by a string, the work done by the centripetal force is zero as the angle between force and displacement is always 900; when a coolie carrying some load on his head moves on a horizontal platform the value of the angle between force and displacement is 900 and hence work done is zero; if you push a wall and it doesn't move, work is not done as there is no displacement; when we hold a bag on our head and walk horizontally such that the angle between the displacement and the gravitational force is 90 degrees, thus, work done is zero.
 An object is moved in a circular path by a string
An object is moved in a circular path by a string
3. Negative Work:
When the force and the direction of movement form an obtuse angle ( θ >900), cos θ is negative, and hence work done is negative.
For example, when a body moves over a rough surface, the direction of frictional force opposes the motion of the body i.e. the angle between force and displacement is 180° and cos180° = -1, so work done is negative; when a body is lifted, the direction of force and displacement is also opposite.
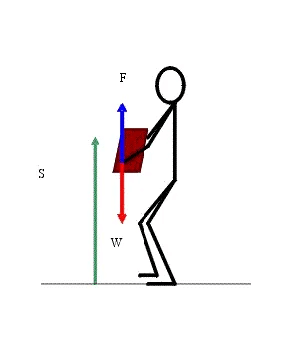 Body lifted up
Body lifted up
Special Cases
(i) If θ = 0°, W = F S cos0° = FS
(ii) If θ =90°, W = F S cos90° = 0
(iii) If θ =180°, W = F S cos180° = −FS
(a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) Work done by gravitational force in the above case.
(c) Work done by friction on a body sliding down an inclined plane.
(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Q1. A block of mass m = 2 kg is pulled by a force F = 40 N upwards through a height (h) = 2m. Find the work done on the block by the applied force F and its weight mg. (g = 10m/s2)
Sol:
Work done by the applied force WF=F h = cos0°
As the angle between force and displacement is 0°
WF= (40)(2)(1)
= 80J
Similarly, work done by its weight
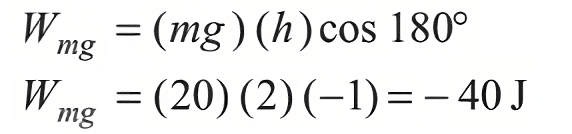
Q2. A block of mass m is kept on a platform which starts from rest with constant acceleration g/2 upward, as shown in fig. work done by normal reaction on the block in time t is: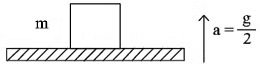
(a) 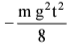
(b) 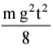
(c) 0
(d) 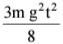
Sol:
Here,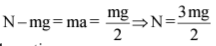
n = normal reaction
Now, work done by normal reaction 'N' on the block in time t,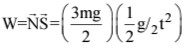
or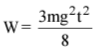
Q3. A force 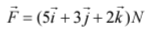 is applied over a particle which displace it from its origin to the point
is applied over a particle which displace it from its origin to the point 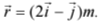 The work done on the particle in joules is
The work done on the particle in joules is
(a) +10
(b) +7
(c) -7
(d) +13
Sol:
Given force 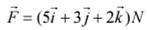
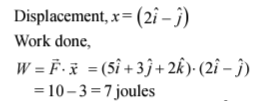
Q4. A block of mass M is pulled along a horizontal surface by applying a force at an angle θ with horizontal. The coefficient of friction between the block and surface is μ. If the block travels with uniform velocity, find the work done by this applied force during a displacement d of the block.
Sol:
The forces acting on the block are shown in Figure. As the block moves with uniform velocity the resultant force on it is zero.


F cos θ = μN ...(i)
F sin θ + N = Mg ...(ii)
Eliminating N from equations (i) and (ii),
F cos θ = n(Mg - Fsin θ)

Work done by this force during a displacement d,

Q5. A particle moving in the x-y plane undergoes a displacement 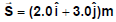 while a constant force
while a constant force 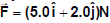 acts on the particle.
acts on the particle.
(a) Calculate the magnitude of the displacement and that of the force.
(b) Calculate the work done by the force.
Sol:

(b) Work done by force, 
 = 10 + 0 + 0 + 6 = 16 N.m = 16 J
= 10 + 0 + 0 + 6 = 16 N.m = 16 J
Q6. A block of mass m is placed on an inclined plane that is moving with constant velocity v in the horizontal direction as shown in the figure. Then find out the work done by the friction in time t if the block is at rest with respect to the incline plane.
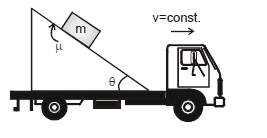
Sol:
F.B.D of the block with respect to ground.


The block is at rest with respect to wedge
⇒ f = mg sinθ
In time t the displacement of the block with respect to ground d = vt
Work done by friction for man A
Wf = (component of friction force along displacement) × displacement
Wf = mgsinθ.vt cos(180°- θ)
Wf = - mg vt cosθ sinθ
Wf for man B = 0 (displacement is zero with respect to man B)
Conservative force
A force is said to be conservative if work done by or against the force in moving a body depends
(a) only on the initial and final positions of the body and
(b) Does not depend on the nature of path followed between the initial and final positions.

- Consider a body of mass m being raised to a height h vertically upwards as shown in above figure. The work done is m g h.
- Suppose we take the body along the path as in (b). The work done during horizontal motion is zero.
- Adding up the work done in the two vertical parts of the paths, we get the result m g h once again.
- Any arbitrary path like the one shown in (c) can be broken into elementary horizontal and vertical portions.
- Work done along the horizontal path is zero.
- The work done along the vertical parts add up to m g h.
- Thus we conclude that the work done in raising a body against gravity is independent of the path taken. It only depends upon the initial and final positions of the body.
We conclude from this discussion that the force of gravity is a conservative force.
Examples of Conservative forces:
(i) Gravitational force, not only due to Earth due in its general form as given by the universal law of gravitation, is a conservative force.
(ii) Elastic force in a stretched or compressed spring is a conservative force.
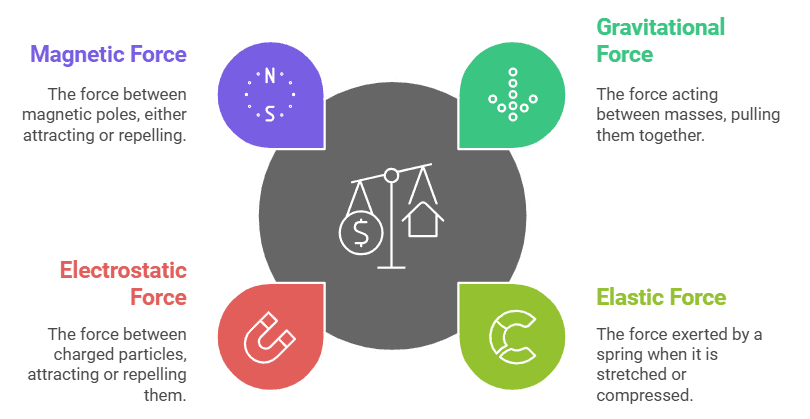 Examples of Conservative Forces
Examples of Conservative Forces
(iii) Electrostatic force between two electric charges is a conservative force.
(iv) Magnetic force between two magnetic poles is a conservative force.
Forces acting along the line joining the centers of two bodies are called central forces.
Gravitational force and Electrostatic forces are two important examples of central forces. Central forces are conservative forces.
Properties of Conservative forces
- Work done by or against a conservative force does not depend upon the nature of the path between initial and final position of the body.
- Work done by or against a conservative force in a round trip is zero.
- If a body moves under the action of a force that does no total work during any round trip, then the force is conservative; otherwise it is non-conservative.
- The concept of potential energy exists only in the case of conservative forces.
- The work done by a conservative force is completely recoverable.
Some Solved Examples are:
I format : (When constant force is given)
Example 1. Calculate the work done to displace the particle from (1, 2) to (4, 5). if 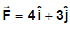
Sol:
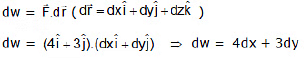
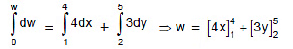
w = (16 - 4) + (15 - 6) = w = 12 + 9 = 21 Joule
II format : (When F is given as a function of x, y, z)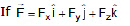 then
then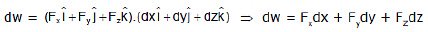
Example 2. An object is displaced from position vector 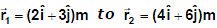 under a force
under a force 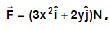 Find the work done by this force.
Find the work done by this force.
Sol. 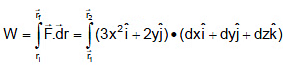
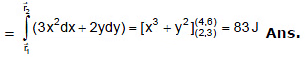
III format : (perfect differential format)
Example 3. 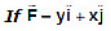 then find out the work done in moving the particle from position (2, 3) to (5, 6).
then find out the work done in moving the particle from position (2, 3) to (5, 6).
Sol: 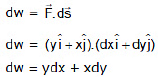
Now ydx + xdy = d(xy) (perfect differential equation)⇒ dw = d(xy)
for total work done we integrate both sides,
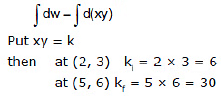
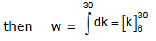
⇒ w = (30 - 6) = 24 Joule
Non-conservative forces
A force is said to be non-conservative if work done by or against the force in moving a body depends upon the path between the initial and final positions.
The frictional forces are non-conservative forces. This is because the work done against friction depends on the length of the path along which a body is moved. It does not depend only on the initial and final positions.
Note: The work done by frictional force in a round trip is not zero.
The velocity-dependent forces such as air resistance, viscous force, magnetic force etc., are non-conservative forces.
Example 4. Calculate the work done by the force to move the particle from (0, 0) to (1, 1) in the following condition
(a) y = x (b) y = x2
Sol. We know that 
dw = ydx ...(1)
In equation (1) we can calculate work done only when we know the path taken by the particle.
either
y = x or y = x2 so now
(a) when y = x
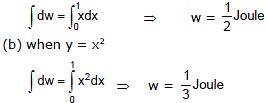
Difference between conservative and Non-conservative forces:
Work Done by a Variable Force
Up to this point, we have focused on the work performed by a constant force, maintaining both its magnitude and direction. Now, let's examine a force that consistently acts in a single direction but may vary in magnitude.
- For convenience, let's align the force along the x-axis.
- Additionally, we'll assume that the magnitude of the force, denoted as F(x), is a known function of x.
- Our objective is to determine the work done by this force when displacing an object from x1 to x2.
- The work done in a small displacement from x to x + dx can be expressed as dW = F(x) dx.
- To calculate the total work, we integrate the elemental work equation mentioned above over the interval from x1 to x2:
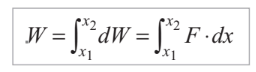
➢ When F as a function of x, y, z
- When the magnitude and direction of a force vary in three dimensions, it can be expressed as a function of the position.
- For a variable force work is calculated for infinitely small displacement and for this displacement force is assumed to be constant.
dW =
- The total work done will be the sum of infinitely small work

- In terms of rectangular components,

Q7. A force F = (4.0 x + 3.0 y
+ 3.0 y ) N acts on a particle that moves in the x-direction from the origin to x = 5.0 m. Find the work done on the object by the force.
) N acts on a particle that moves in the x-direction from the origin to x = 5.0 m. Find the work done on the object by the force.
Sol: Here the work done is only due to the x component of force because displacement is along the x-axis.
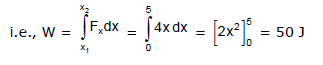
Q8. A force F = 0.5x + 10 acts on a particle. Here F is in Newton and x is in metre. Calculate the work done by the force during the displacement of the particle from x = 0 to x = 2 metre.
Sol: The small amount of work done, dW in giving a small displacement is given by
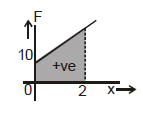

Total work done, W

➢ When F is given as a function of Time(t)
When the force, denoted as F, is given as a function of time, denoted as t, it means that the magnitude of the force acting on an object can change over time. In this case, we are interested in finding the work done by this time-dependent force in moving an object from one position to another.
Here is an example showing how to solve this:
Q9. The force F = 2t2 is applied on the 2 kg block. Then find out the work done by this force in 2 sec. Initially at time t = 0, the block is at rest.
Sol:




Let the displacement of the block be dx from t = t to t = t +dt then, work done by the force F in this time interval, dt is:




Work Done by Area Under F-S or F -x Graph
Work done by a force can be obtained from the area under the F-x graph. Unlike the integration
W = ∫Fdx= area under F- x graph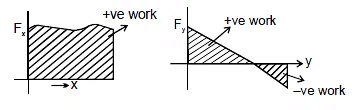

- Work done by a force can be obtained from the area under the F-x graph.
- Unlike the integration method of finding work done in which the sign of work done automatically comes after integration, in this method area of the graph will only give us the magnitude of work done.
- If force and displacement have the same sign, work done will be positive and if both have opposite signs, work done is negative.
Q10. Force acting on a particle varies with x as shown in the figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
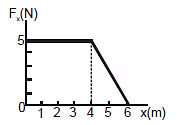
Sol: The work done by the force is equal to the area under the curve from x = 0 to x = 6.0 m.
This area is equal to the area of the rectangular section from x = 0 to x = 4.0 m plus the area of the triangular section from x = 4.0 m tox = 6.0 m. The area of the rectangle is (4.0) (5.0) N.m = 20 J, and the area of the triangle is  (2.0), (5.0) N.m = 5.0 J. Therefore, the total work done is 25 J.
(2.0), (5.0) N.m = 5.0 J. Therefore, the total work done is 25 J.
Q11. A person pushes a box on a rough horizontal platform surface. He applies a force of 200 N over a distance of 15 m. Thereafter, he gets progressively tired and his applied force reduces linearly with distance to 100 N. The total distance through which the box has been moved is 30 m.
What is the work done by the person during the total movement of the box ?
(a) 3280 J
(b) 2780 J
(c) 5690 J
(d) 5250 J
Ans: (d) 5250 J
Explanation:
The given situation can be drawn graphically as
shown in figure.
Work done = Area under F-x graph
= Area of rectangle ABCD + Area of trapezium BCFE
Q12. Con sider a force 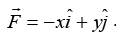 The work done by this force in moving a particle from point A(1, 0) to B(0, 1) along the line segment is: (all quantities are in SI units)
The work done by this force in moving a particle from point A(1, 0) to B(0, 1) along the line segment is: (all quantities are in SI units)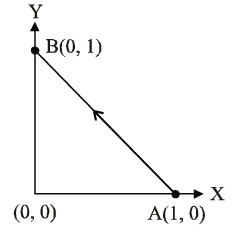
(a) 2 J
(b) 1/2 J
(c) 1 J
(d) 3/2 J
Ans: (c) 1 J
Explanation:
Q13. When a rubber band is stretched by a distance x, it exerts restoring force of magnitude F = ax + bx2 where a and b are constants. The work done in stretching the unstretched rubber band by L is:
(a) aL2 + bL3
(b) 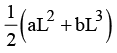
(c) 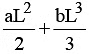
(d) 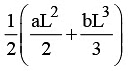
Ans: (c) 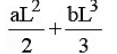
Explanation:
Work done in stretching the rubber band by a distance dx is
dW = F dx = (ax + bx2)dx
Integrating both sides,
Work Energy Theorem
If the resultant or net force acting on a body is Fnet then Newton's second law states that
Fnet = ma ...(1)
If the resultant force varies with x, the acceleration and speed also depend on x.


Work done by net force Fnet in displacing a particle equals to the change in kinetic energy of the particle.
i.e. we can write eq. (3) in following way
(W.D)C + (W.D)N.C + (W.D)ext. + (W. D)pseudo
= ΔK ...(4)
where (W.D)C = work done by conservative force
(W. D)N.C = work done by non conservative force.
(W.D)ext = work done by external force
(W.D)pseudo = work done by pseudo force, we know that
we know that
(W.D)c = - ΔU
⇒ - ΔU + (W.D)N.C + (W.D)ext (W.D)pseudo = ΔK
= (W.D)N.C + (W.D)ext + (W.D)pseudo - (kf + uf) - (ki + ui)
∴ k 4+ u = Mechanical energy.
=> work done by forces (except conservative forces) = change is mechanical energy.
If (W.D)N.C = (W.D)ext = (W.D)pseudo = 0
= Kf + Uf = Ki + Ui
Initial mechanical energy = final mechanical energy
This is called mechanical energy conservation law.
Questions Based on Work Energy Theorem
(A) When only one conservative force is actingExample 5. The block shown in the figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m.
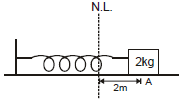
Sol:
In the above problem only one conservative force (spring force) is working on the block so from mechanical energy conservation

at A block is at rest so ki = 0

At position B if speed of the block is v then

Putting the above values in equation (i), we get

Example 6. A block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
Sol:
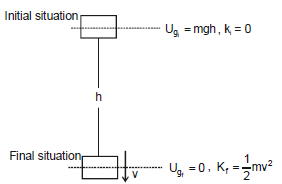
Figure shows the complete description of the problem only one conservative force is working on the block. So from mechanical energy conservation
kf + uf = ki + ui
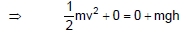
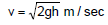
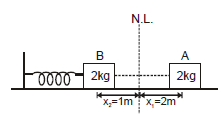
(B) When two conservative force are acting in problem.
Example 7. One end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37º with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. [sin 37º = 3/5]

Sol: If l is the stretched length of the spring, then from figure


Now, taking point B as reference level and applying law of conservation of mechanical energy between A and B,
EA = EB
or 
[as for, B, h = 0 and y = 0]
or 


Example 8. The block shown in figure is released from rest and initially the spring is at its natural length. Write down the energy conservation equation. When the spring is compressed by l1 ?

Sol: Here two conservative forces are included in the problem.
(i) Gravitational force (ii) spring force
We assume zero gravitational potential energy at A as shown in figure.
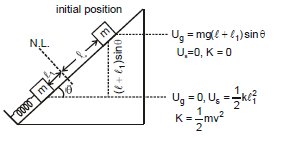
from mechanical energy conservation
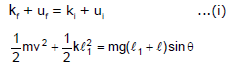
(C) When only one non conservative force is included in problem.
Example 9. Find out the distance travelled by the block as shown in figure. If the initial speed of the block is v and m is the friction coefficient between the surface of block and ground.

Sol. Applying work energy theorem, we get
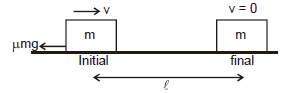
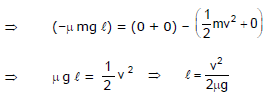
(D) When both conservative and non-conservative force in the problem
Example 10. A particle slides along a track with elevated ends and a flat central part as shown in figure. The flat portion BC has a length l = 3.0 m. The curved portions of the track are frictionless. For the flat part the coefficient of kinetic friction is mk = 0.20, the particle is released at point A which is at height h = 1.5 m above the flat part of the track. Where does the particle finally comes to rest?
Sol: As initial mechanical energy of the particle is m g h and final is zero, so loss in mechanical energy will be m g h. This mechanical energy is lost in doing work against friction in the flat part,
So, loss in mechanical energy = work done against friction
or m g h = m g s i.e., s =  =
=  = 7.5 m
= 7.5 m
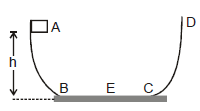
After starting from B the particle will reach C and then will rise up till the remaining KE at C is converted into potential energy. It will then again descend and at C will have the same value as it had when ascending, but now it will move from C to B. The same will be repeated and finally the particle will come to rest at E such that
BC + CB + BE = 7.5
or 3 + 3 + BE = 7.5
i.e., BE = 1.5
So, the particle comes to rest at the centre of the flat part.
Example 11. A 0.5 kg block slides from the point A on a horizontal track with an initial speed 3 m/s towards a weightless horizontal spring of length 1 m and force constant 2 N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as 0.22 and 0.20 respectively. If the distance AB and BD are 2 m and 2.14 m respectively, find the total distance through which the block moves before it comes to rest completely. [g = 10 m/s2]
Sol: As the track AB is frictionless, the block moves this distance without loss in its initial
KE =  =
=  × 0.5 × 32 = 2.25 J. In the path BD as friction is present, so work done against friction
× 0.5 × 32 = 2.25 J. In the path BD as friction is present, so work done against friction
= mk mgs = 0.2 × 0.5 × 10 × 2.14 = 2.14 J
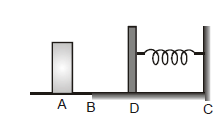
So, at D the KE of the block is = 2.25 - 2.14 = 0.11 J.
Now, if the spring is compressed by x
0.11 =  × k × x2+ mk mgx
× k × x2+ mk mgx
i.e., 0.11 =  × 2 × x2 0.2 × 0.5 × 10x
× 2 × x2 0.2 × 0.5 × 10x
or x2 + x - 0.11 = 0
which on solving gives positive value of x = 0.1 m
After moving the distance x = 0.1 m the block comes to rest. Now the compressed spring exerts a force :
F = kx = 2 × 0.1 = 0.2 N
on the block while limiting frictional force between block and track is fL = ms mg = 0.22 × 0.5 × 10 = 1.1 N.
Since, F < fL. The block will not move back. So, the total distance moved by block
= AB + BD + 0.1
= 2 + 2.14 + 0.1
= 4.24 m
Important Examples:
Example 12. A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle q it slides.
Sol: We solve the above problem with respect to the sphere. So apply a pseudo force on the particle

Now from work energy theorem.
work done by ma = change in mechanical energy
⇒ ma R sinθ = (kf + uf) - (ki + ui)
maR sinθ =  ⇒
⇒  = maR sinθ + mgR (1 - cosθ)
= maR sinθ + mgR (1 - cosθ)
⇒ v2 = 2R(a sinθ + g - g cosθ) ⇒ v = [2R (a sinθ + g - g cosθ)]1/2 m/sec
Example 13. In the arrangement shown in figure mA = 4.0 kg and mB = 4.0 kg. The system is released from rest and block B is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of friction between the block and the table.
Neglect friction elsewhere. (Take g = 10 m/s2)
Sol: From constraint relations, we can see that
vA = 2 vB
Therefore, vA = 2(0.3) = 0.6 m/s
as vB = 0.3 m/s (given)
Applying Wnc = DU + DK
we get - m mA g SA = - mB g SB +  mAvA2 +
mAvA2 +  mBvB2
mBvB2
Here, SA = 2SB = 2m as SB = 1 m (given)
- m(4.0) (10) (2) = - (1) (10) (1) + (4) (0.6)2 +
(4) (0.6)2 +  (1) (0.3)2
(1) (0.3)2
or - 80 m = - 10 + 0.72 + 0.045 or 80m = 9.235 or m = 0.115
Different situations
(A) A body moving inside a hollow tube or sphere
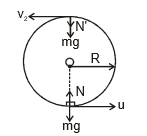
The previous discussion holds good for this case, but instead of tension in the string we have the normal reaction of the surface. If N is the normal reaction at the lowest point, then the condition for the body to complete the circle holds for this case also. All other equations (can be) similarly obtained by replacing tension T by normal reaction N.
for the body to complete the circle holds for this case also. All other equations (can be) similarly obtained by replacing tension T by normal reaction N.
(B) When Body is attached to a rod of length R
In this case since the body is attached to a rigid rod. The body can not leave the circular path.
Therefore, if the speed of the body becomes zero before the highest point C. It's motion will be oscillatory about the centre of the rod.
Condition for completing the circle:
If the body just reaches the highest point then it will completes the vertical circle
Applying energy conservation between the lowest and highest point of circle, we get
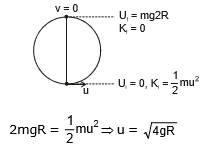
So, If the velocity at point A is greater than equal to  then body will compete the vertical circle.
then body will compete the vertical circle.
(C) Vertical Motion in a Dual Ring
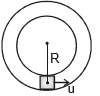
This system will behave as the previous system. So umin to complete vertical circle 
Angle at which the normal reaction on the body will change its direction from inward to outward the ring is given by


(D) Body Moving on a Spherical Surface
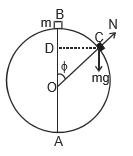
The small body of mass m is placed on the top of a smooth sphere of radius R and the body slides down the surface.
At any instant, i.e., at point C the forces are the normal reaction N and the weight mg. The radial component of the weight is mgcos f acting towards the centre. The centripetal force is
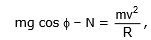

The body flies off the surface at the point where N becomes zero.

To find v, we use conservation of energy

From equation (ii) and (iii) we get

This gives the angle at which the body goes of the surface. The height from the ground of that point AD = R(1 + cos φ)

|
97 videos|379 docs|103 tests
|
FAQs on Introduction to Work and Work Energy Theorem - Physics Class 11 - NEET
| 1. What is the definition of work in physics? |  |
| 2. How is work done by a constant force calculated? |  |
| 3. What is the difference between work done by a constant force and work done by a variable force? |  |
| 4. How can the work-energy theorem be explained? |  |
| 5. How do you determine the work done from a force vs. displacement graph? |  |

|
Explore Courses for NEET exam
|

|