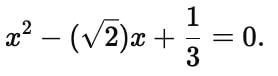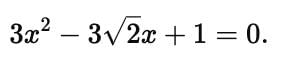Important Definitions & Formulas: Polynomials | Mathematics (Maths) Class 10 PDF Download
The chapter "Polynomials" is really important for learning the basics of algebra and how to use them to solve different math problems. It's like the foundation for solving all kinds of math questions in the future.
In this document, you'll find Class 10 Math Formulas related to Polynomials that can help you do well in your board exams and other important competitive exams.
Important Definitions
1. Polynomials
An algebraic expression of the form p(x) = a₀ + a₁ x + a₂ x2 + a₃ x3 + ...... + an xn, in which the variables involved have only non-negative integral exponents, is called a polynomial in x of degree n.
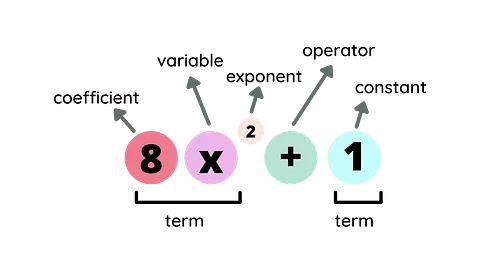 Polynomial
Polynomial
Note:
In the polynomial a₀ + a₁ x + a₂ x2 + a₃ x3 + ...... + an xn
a₀, a₁ x, a₂ x2, a₃ x3 ..... an - 1 xn - 1, anxn are terms.
a₀, a₁, a₂, ..... an - 1, an are the co-efficients of x0, x1, x2, ....., xn-1, xn respectively.
2. Degree of a Polynomial
The highest power of the variable in a polynomial is called its degree.
 Example:
Example:
5x + 3 is a polynomial in x of degree 1.
p(y) = 3y2 + 4y - 4 is a polynomial in y of degree 2.
- Linear Polynomial: A polynomial of degree 1 is called a linear polynomial. A linear polynomial is generally written as ax + b (a ≠ 0), where a, and b are real coefficients.
- Quadratic Polynomial: A polynomial of degree 2 is called a quadratic polynomial. A quadratic polynomial is generally written as ax2 + bx + c (a ≠ 0), where a, b and c are real coefficients.
- Cubic Polynomial: A polynomial of degree 3 is called a cubic polynomial. A cubic polynomial is generally written as ax3 + bx2 + cx + d (a ≠ 0), where a, b, c and d are real coefficients.
Examples: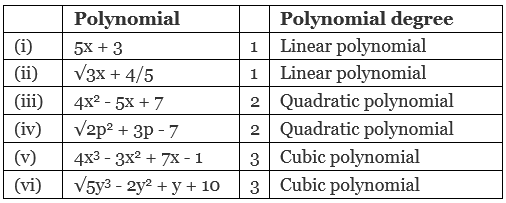
Value of a Polynomial at a Given Point
If p (x) is a polynomial in x and ‘a’ is a real number. Then the value obtained by putting x = a in p (x) is called the value of p (x) at x = a.
Example: Let p(x) = 5x2 - 4x + 2 then its value at x = 2 is given by
p(2) = 5 (2)2 - 4 (2) + 2 = 5 (4) - 8 + 2 = 20 - 8 + 2 = 14
Thus, the value of p(x) at x = 2 is 14.
3. Zeroes of a Polynomial
A real number ‘a’ is said to be a zero of the polynomial p (x), if p (a) = 0.
Example: Let p (x) = x2 - x - 2 Then p (2) = (2)2 - (2) - 2 = 4 - 4 = 0,
and p (-1) = (-1)2 - (-1) - 2 = 2 - 2 = 0
∴ (-1) and (2) are the zeroes of the polynomial x2 - x - 2.
Note:
I. A linear polynomial has at the most one zero.
II. A quadratic polynomial has at the most two zeroes.III. In general a polynomial of degree n has at the most n zeroes.
4. Geometrical Meaning of the Zeroes of a Polynomial
First, we consider a linear polynomial p (x) = ax + b.
Let ‘k’ be a zero, then p(k) = ak + b = 0
⇒ ak + b = 0
⇒ ak = - b or

The graph of a linear polynomial is always a straight line. It may or may not pass through the x-axis. In case the graph line is passing through a point on the x-axis, then the y-coordinate of that point must be zero. In general, for a linear polynomial ax + b = 0, (a ≠ 0), the graph is a straight line that can intersect the x-axis at exactly one point, namely, 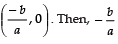 is the zero of the polynomial ax + b.
is the zero of the polynomial ax + b.
In the given figure, CD is meeting x-axis at x = -1.
∴ Zero of ax + b is -1.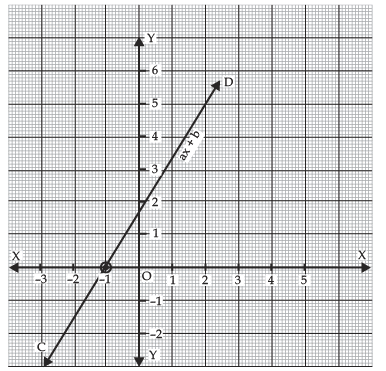
Note:
A zero of a linear polynomial is the x-coordinate of the point, where the graph intersects the x-axis.
Important Methods and Formulas
1. Graph of a Quadratic Polynomial
The graph of ax2 + bx + c, (a ≠0) is a curve of ∪ shape, called a parabola.
- If a > 0 in ax2 + bx + c, the shape of the parabola is ∪ (opening upwards).
- If a < 0 in ax2 + bx + c, the shape of the parabola is ∩ (opening downwards).
In the given figure, the graph of a quadratic polynomial x2 - 3x - 4 is shown. It intersects x-axis at (-1, 0) and (4, 0). Therefore, its zeroes are -1 and 4. Here, a > 0, so the graph opens upwards.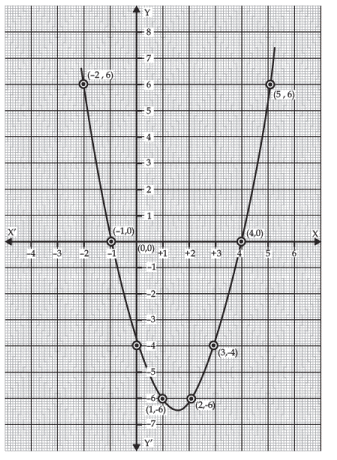
Whereas the following figure is a graph of the polynomial - x2 + x + 6. Since it intersects the x-axis at (3, 0) and (-2, 0). Therefore, the zeroes of - x2 + x + 6 are -2 and 3.
Here a < 0, so the parabola opens downwards.
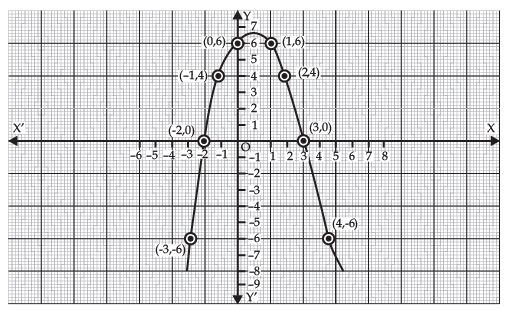
Note: In the case of Quadratic polynomial - at most 2 zeroes, Cubic polynomial - at most 3 zeroes, Biquadratic polynomial - at most 4 zeroes.
2. Relationship between Zeroes and Coefficients of Polynomials
- For a quadratic polynomial,
p(x) = ax2 + bx + c,
Sum of Roots: α + β = -b/a
Product of Roots: αβ = c/a
where α and β are the zeroes of the polynomial p(x) = ax2 + bx + c - For a cubic polynomial,
p(x) = ax3 + bx2 + cx + d,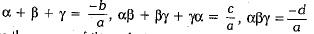
where α, β and γ are the zeroes of the polynomial p(x) = ax3 + bx2 + cx + d.
3. Division Algorithm (Deleted from NCERT Textbook)
To divide one polynomial by another, follow the steps given below.
Step 1: Arrange the terms of the dividend and the divisor in the decreasing order of their degrees.
Step 2: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor Then carry out the division process.
Step 3: The remainder from the previous division becomes the dividend for the next step. Repeat this process until the degree of the remainder is less than the degree of the divisor.
|
127 videos|655 docs|84 tests
|
FAQs on Important Definitions & Formulas: Polynomials - Mathematics (Maths) Class 10
| 1. What is the degree of a polynomial? |  |
| 2. How can we find the zeroes of a polynomial? |  |
| 3. How is the graph of a quadratic polynomial represented? |  |
| 4. What is the relationship between the zeroes and coefficients of a polynomial? |  |
| 5. Why was the Division Algorithm deleted from the NCERT textbook? |  |