Percentage And Its Applications | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| Percentage |

|
| Percentage Formula |

|
| Percentage Chart |

|
| Percentage Questions |

|
| Word Problems |

|
| Difference between Percentage and Percent |

|
Percentage
In mathematics, a percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by the whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100. It is represented by the symbol “%”.
Examples of percentages are:
- 10% is equal to 1/10 fraction
- 20% is equivalent to ⅕ fraction
- 25% is equivalent to ¼ fraction
- 50% is equivalent to ½ fraction
- 75% is equivalent to ¾ fraction
- 90% is equivalent to 9/10 fraction
Percentages have no dimension. Hence it is called a dimensionless number. If we say, 50% of a number, then it means 50 per cent of its whole.
Percentages can also be represented in decimal or fraction form, such as 0.6%, 0.25%, etc. In academics, the marks obtained in any subject are calculated in terms of percentage. Like, Ram has got 78% of marks in his final exam. So, this percentage is calculated on account of the total marks obtained by Ram, in all subjects to the total marks.
Percentage Formula
- To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100.
- Percentage formula = (Value/Total value) × 100
- Example: 2/5 × 100 = 0.4 × 100 = 40 per cent
How to calculate the percentage of a number?
To calculate the percentage of a number, we need to use a different formula such as:
P% of Number = X
where X is the required percentage.
If we remove the % sign, then we need to express the above formulas as;
P/100 * Number = X
Example: Calculate 10% of 80.
Let 10% of 80 = X
10/100 * 80 = X
X = 8
Percentage Difference Formula
If we are given with two values and we need to find the percentage difference between these two values, then it can be done using the formula:

For example, if 20 and 30 are two different values, then the percentage difference between them will be:
% difference between 20 and 30 =

Percentage Increase and Decrease
The percentage increase is equal to the subtraction of the original number from a new number, divided by the original number and multiplied by 100.
% increase = [(New number – Original number)/Original number] x 100
where,
increase in number = New number – original number
Similarly, a percentage decrease is equal to the subtraction of a new number from the original number, divided by the original number and multiplied by 100.
% decrease = [(Original number – New number)/Original number] x 100
Where decrease in number = Original number – New number
So basically if the answer is negative then there is a percentage decrease.
Example: Let a bag contain 2 kg of apples and 3kg of grapes. Find the ratio of quantities present, and the percentage occupied by each.
Solution:
The number of apples and grapes in a bag can be compared in terms of their ratio, i.e. 2:3.
The actual interpretation of percentages can be understood as follows:
The same quantity can be represented in terms of the percentage occupied, which can be done as given below.
Total quantity present = 5 kg
Ratio of apples (in terms of total quantity) = 2/5
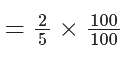
From the definition of percentage, it is the ratio that is expressed per hundred,
(1/100) = 1%
Thus, Percentage of Apples = (2/5) × 100 = 40%
Percentage of Grapes = (3/5) × 100 = 60%
Percentage Chart
The percentage chart is given here for fractions converted into percentages.
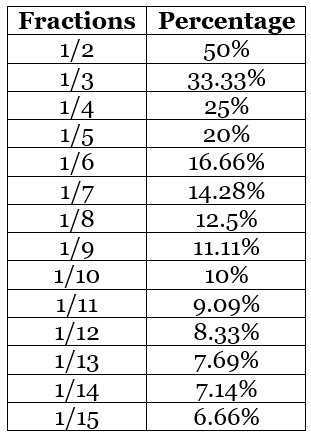
Converting Fractions to Percentage
A fraction can be represented by a/b.
Multiplying and dividing the fraction by 100, we have
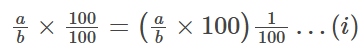
From the definition of percentage, we have;
(1/100) = 1%
Thus, equation (i) can be written as:
(a/b) × 100%
Therefore, a fraction can be converted to a percentage simply by multiplying the given fraction by 100.
Percentage Questions
Q1: If 16% of 40% of a number is 8, then find the number.
Solution: Let X be the required number.
Therefore, as per the given question,
(16/100) × (40/100) × X = 8
So, X = (8 × 100 × 100) / (16 × 40)
= 125
Q2: What percentage of 2/7 is 1/35 ?
Solution: Let X% of 2/7 is 1/35.
∴ [(2/7) / 100] × X = 1/35
⇒ X = (1/35) × (7/2) × 100
= 10%
Q3: Which number is 40% less than 90?
Solution: Required number = 60% of 90
= (90 x 60)/100
= 54
Therefore, the number 54 is 40% less than 90.
Q4: The sum of (16% of 24.2) and (10% of 2.42) is equal to what value?
Solution: As per the given question ,
Sum = (16% of 24.2) + (10% of 2.42)
= (24.2 × 16)/100 + (2.42 × 10)/100
= 3.872 + 0.242
= 4.114
Word Problems
Q1: A fruit seller had some apples. He sells 40% apples and still has 420 apples. Originally, he had how many apples?
Solution: Let he had N apples, originally.
Now, as per the given question, we have;
(100 – 40)% of N = 420
⇒ (60/100) × N = 420
⇒ N = (420 × 100/60) = 700
Q.2: Out of two numbers, 40% of the greater number is equal to 60% of the smaller. If the sum of the numbers is 150, then the greater number is?
Solution: Let X be the greater number.
∴ Smaller number = 150 – X {given that the sum of two numbers is 150}
According to the question,
(40 × X)/100 = 60(150 – X)/100
⇒ 2p = 3 × 150 – 3X
⇒ 5X = 3 × 150
⇒ X = 90
Difference between Percentage and Percent
- The words percentage and percent are related closely to each other.
- Percent ( or symbol %) is accompanied by a specific number.
- E.g., More than 75% of the participants responded with a positive response to abjure.
- The percentage is represented without a number.
- E.g., The percentage of the population affected by malaria is between 60% and 65%.
Fractions, Ratios, Percents and Decimals are interrelated with each other. Let us look at the conversion of one form to another: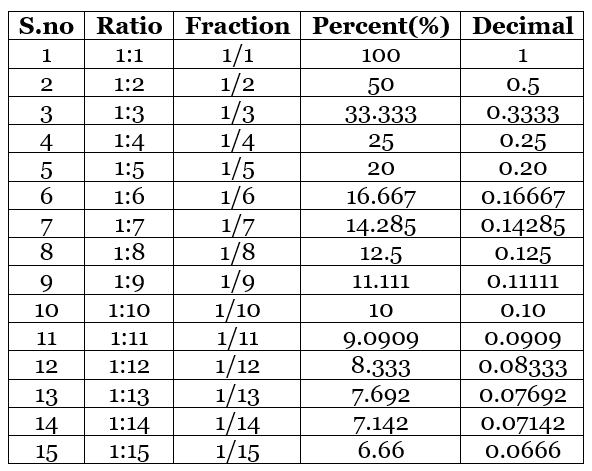
Percentage in Maths
Every percentage problem has three possible unknowns or variables :
- Percentage
- Part
- Base
In order to solve any percentage problem, you must be able to identify these variables.
Look at the following examples. All three variables are known:
Example 1: 70% of 30 is 21
- 70 is the percentage.
- 30 is the base.
- 21 is the part.
Example 2: 25% of 200 is 50
- 25 is the percent.
- 200 is the base.
- 50 is the part.
Example 3: 6 is 50% of 12
Percentage Tricks
To calculate the percentage, we can use the given below tricks.
x % of y = y % of x
Example: Prove that 10% of 30 is equal to 30% of 10.
Solution: 10% of 30 = 3
30% of 10 = 3
Therefore, they are equal i.e. x % of y = y % of x holds true.
Marks Percentage
Students get marks in exams, usually out of 100. The marks are calculated in terms of per cent. If a student has scored out of total marks, then we have to divide the scored marks by total marks and multiply by 100. Let us see some examples here:
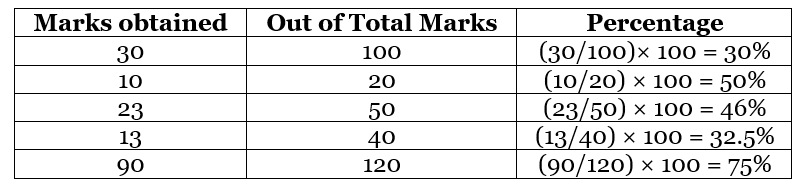
|
57 videos|108 docs|73 tests
|
FAQs on Percentage And Its Applications - Quantitative Techniques for CLAT
| 1. What is the formula to calculate percentage? |  |
| 2. How do you convert a percentage into a decimal? |  |
| 3. What are some common applications of percentages in daily life? |  |
| 4. What is the difference between percentage and percent? |  |
| 5. How can I solve percentage word problems effectively? |  |

|
Explore Courses for CLAT exam
|

|



















