Rate Law and Integrated Rate Equations | Chemistry Class 12 - NEET PDF Download
What is Rate of a Reaction ?
The Rate of a Chemical Reaction is a measure of how quickly reactants are transformed into products. It can be expressed in various ways, depending on the specific details of the reaction. Generally, it is defined as the change in concentration of a reactant or product per unit of time.
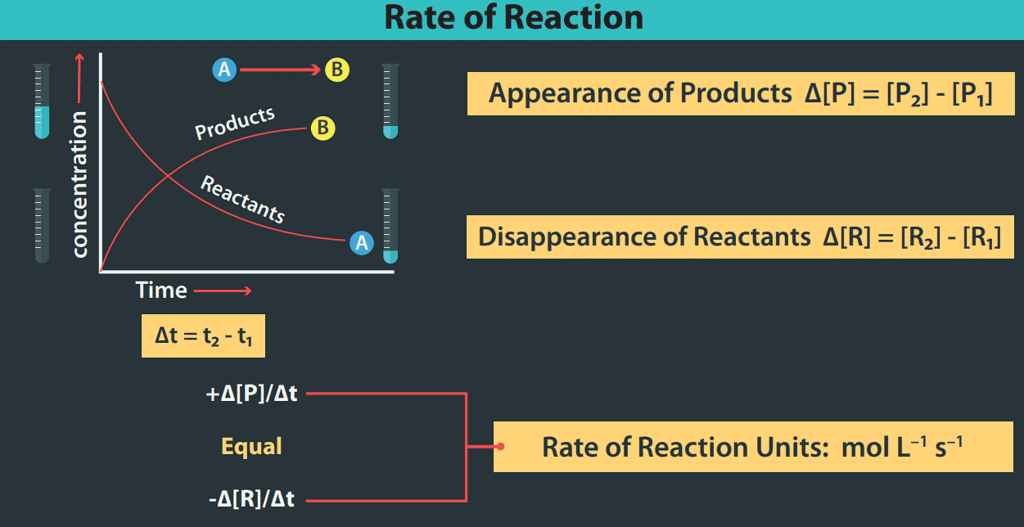
Mathematically, the Rate of a Reaction (R) can be expressed using the following general formula:
- The rate of reaction refers to the speed at which the products are formed from the reactants in a chemical reaction.
- It gives some insight into the time frame under which a reaction can be completed. For example, the reaction rate of the combustion of cellulose in fire is very high and the reaction is completed in less than a second.
- In general, for a reaction: R → P, the behaviour of the concentration of the reactant and product, as the reaction proceeds is shown graphically:
From the graph, it is clear that the concentration of the reactant decreases and that of the product increases as the reaction proceeds and the rate of the change of the concentration of the reactant as well as that of the product is also changing.
Example 1: Suppose the concentration of a reactant A changes from 0.4 M to 0.1 M in a time interval of 20 seconds. The rate of the reaction (r) can be calculated using formula:
r= Δ[A]/Δt
r = (0.1M−0.4M)/20s
r= −0.3M/20s
r=−0.015M/s
Note: The negative sign indicates a decrease in the concentration of the reactant, which is typical for reactants in a chemical reaction.So, in this example, the rate of the reaction is −0.015M/s
What is Rate Law?
The rate law (also known as the rate equation) for a chemical reaction is an expression that provides a relationship between the rate of the reaction and the concentrations of the reactants participating in it.
Formula and Unit of Rate of Reaction
The differential rate equations of chemical reaction in kinetics depend on the change of concentration of reactants and products at any instant in time.Let a simple kinetic reaction,
A → B
The rate in terms of reactant = − d[A]/dt
The rate in terms of product = d[B]/dt
- Negative signs are used to show the decrease in the concentration of reactants with time. But the rate is always a positive quantity and it decreases with time.
- A complication arises if we consider the reaction,
A + 2B → 3C + D - In this chemical reaction rate of decrease of B is twice the rate of decrease of A. To resolve this complication we mention the rate of reaction in terms of a particular component given below the picture,

- Unit of Rate of Reaction: In physical chemistry, the rate of reactions in chemical kinetics is defined as the rate of change of concentration of reactants and products at any instant in time. The unit of rate = unit of concentration/unit of time. Therefore, the unit of the rate of the reaction is mol lit−1 s−1 or mol m−3 s−1.
Example 2: In a chemical reaction, N2 + 3H2 → 2 NH3 the rate of (d[NH3]/dt) = 2 × 10−4. How to calculate the value of (−d[H2]/dt) by kinetics equation?
Answer: From the rate equation for the formation of ammonia from nitrogen and hydrogen,
d[H2]/dt = (3/2) × 2 × 10−4 mol lit−1 sec−1
= 3 × 10−4 mol lit−1 sec−1
Example 3: What do you understand by the rate law and rate constant of a reaction?
Answer: The rate of reaction is shown to be dependent on the concentration terms of reactant A and reactant B.
Then, Rate of reaction ∝ [A]α [B]β
or Rate = K [A]α [B]β
This expression is termed Rate law.
Example 4: The rate of formation of NO(g) in the reaction NOBr(g)→ NO(g) Br2(g) is found to be 1.6 × 10-4 M/s. Find the rate of overall reaction rate and rate of consumption of NOBr.
We have :
1.6 × 10-4 M/s.
First write a balanced chemical equation. 2NOBr(g) → 2NO(g) Br2(g)
Now, Rate of overall reaction =
=
=
= 0.8 × 10-4 M/s
Rate of consumption of NOBr = -
= 1.6 × 10-4 M/s
What is Order of a Reaction?
The order of a reaction refers to the power to which the concentration of a reactant is raised in the rate equation (rate law) for that particular reaction.
For example consider the reaction : aA+ bB → cC +dD. The differential rate law is written as :
Rate =  =
=  =
=  =
=  = kr[A]m[B]n
= kr[A]m[B]n
where kr is called as rate constant of the reaction or velocity constant or specific Reaction rate.
k is a characteristic of a reaction at a given temperature. It changing only when the temperature changes.
The powers m and n are integers or fractions. m is called as order of reaction with respect to A and n is called as order of reaction with respect to B. The overall order of reaction = m + n
Hence, the sum of powers of the concentration of the reactants in the rate law expression is called the order of that chemical reaction.

- The values of m and n are calculated from the experimental data obtained for a reaction and the powers m and n are not related to the stoichiometric coefficients of the reactants
- Order can be fractional, zero or negative.
For example consider the following reaction :
(i) H2(g) Br2(g) → 2 HBr (g) rate = k[H2] [Br2]1/2 (by experiment), order of reaction = 1 + 1/2 = 3/2
(ii) CH3CHO(g) → CH4(g) CO(g), rate = k[CH3CHO]3/2 , order of reaction = 3/2
Units of Rate Constant k:
In general, the rate law for a nth order reaction can be taken as :
where k: rate constant; c : concentration and n : order of reaction
⇒  ⇒ Units of k º (mol/L)1-n (time)-1
⇒ Units of k º (mol/L)1-n (time)-1
- For a 'zero' order reaction (n = 0) : Units of k = (mol/L)1 (time)-1 or mol/L/sec
- For a first order reaction (n = 1) : Units of k º (time)-1 e.g. sec-1, min-1, hrs-1 etc.
- For a second order reaction (n = 2) : Units of k º (mol/L)-1 (time)-1 or L/mol/sec.
Example 5: The rate constant of a reaction is k=3.28×10-4 s-1. Find the order of the reaction.
a) Zero order
b) First order
c) Second order
d) Third order
Answer: b) First order
Explanation: Given, k= 3.28×10-4 s-1
The standard formula for calculating rate constant units is k=(mol L-1)1-ns-1, where ‘n’ is the reaction order. The value of ‘n’ must be 1 for (mol L-1)1-ns-1 to be s-1. As a result, k=3.28×10-4s-1 denotes a first-order reaction.
Molecularity of a Reaction
Molecularity refers to the number of molecules (or ions) that participate as reactants in an elementary reaction.
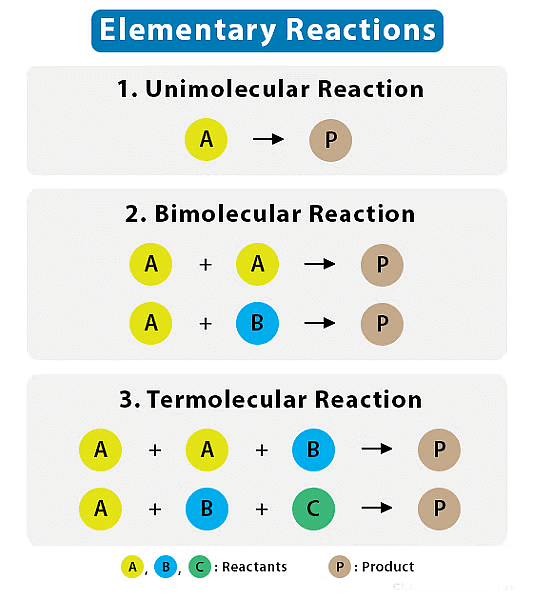
- Elementary reaction is a simple, single-step chemical reaction that involves a small number of reactant species and leads directly to the formation of products.
- Molecularity is a concept used specifically for elementary reactions, and it is not applicable to overall or complex reactions.
The molecularity of a reaction is often classified into three categories:
1. Unimolecular (Molecularity = 1)
- In a unimolecular reaction, a single molecule is involved in the elementary reaction. The rate equation for a unimolecular reaction is often expressed as: Rate=k[A]
- An example of a unimolecular reaction is a first-order reaction, where a single molecule undergoes a reaction, and the rate is directly proportional to its concentration.
- Cyclopropane → propene
- O3(g) → O2(g) + O(g)
- N2O5(g) → N2O4(g) +1/2O2(g)
2. Bimolecular (Molecularity = 2)
- In a bimolecular reaction, two molecules come together to react in a single step. The rate equation for a bimolecular reaction is often expressed as:
Rate=k[A][B]
- An example of a bimolecular reaction is a second-order reaction, where the rate is proportional to the product of the concentrations of two reactants.
- NO(g) + O3 (g) → NO2(g)+ O2(g)
- 2HI(g) → H2(g) I2(g)
3. Termolecular (Molecularity = 3)
- In a termolecular reaction, three molecules collide and react simultaneously in a single step. Termolecular reactions are relatively rare because they require the simultaneous collision of three reactant molecules, which is less likely to occur. They are more common in gas-phase reactions.
- Termolecular reactions are not as frequently encountered as unimolecular or bimolecular reactions.
It's important to note that molecularity is a theoretical concept used to describe elementary reactions. In more complex reactions, which involve multiple elementary steps, the reaction order and molecularity may not be the same. Overall reaction orders are determined experimentally, while molecularity is a concept used to describe the individual elementary steps of a reaction mechanism.
Difference Between Order and Molecularity of a Reaction

Example 6: From the rate laws for the reactions given below, determine the order with respect to each species and the overall order:
(i) 2HCrO4- + 6I- + 14H → 2Cr3 + 3I2+8H2O, Rate = k[HCrO4-] [I-]2 [H ]2
(ii) H2O2 +2I- +2H → I2 +2H2O, Rate = k[H2O2] [I-]
Sol. (i) The order of the reaction with respect to [HCrO4-] is 1; with respect to [I-] is 2 and with respect to [H ] is 2. The overall order of the reaction is 1 +2 +2 = 5
(ii) The order of the reaction with respect to [H2O2] is 1 and with respect to [I-] is 1. The overall order of the reaction is 1 +1= 2.
- In (i) stoichiometric coefficient of I- is 6 whereas the power coefficient (n) in the rate law is 2.
- Reaction (i) may not take place in a single step. It may not be possible for all the 22 molecules to be in a state to collide with each other simultaneously. Such a reaction is called a complex reaction.
- A complex reaction takes place in a series of a number of elementary reactions.
What are Integrated Rate Equations?
Integrated rate equations are mathematical expressions that relate the concentrations of reactants and/or products to time for a chemical reaction.

These equations are obtained by integrating the rate laws, which describe how the rate of a reaction depends on the concentrations of reactants.
- The integrated rate equations provide a way to directly relate concentration and time, allowing for the determination of reaction kinetics and the calculation of reaction constants.
- The form of the integrated rate equation depends on the order of the reaction, which is determined experimentally.
- The three most common types of reaction orders are zero order, first order, and second order. Here are the integrated rate equations for each:
(i) Zero Order Reactions
The rate law for zero order reactions (n = 0) is written as :



- 
- 
[A]o - [A] = kt
 =
= 
Half-life (t 1/2) of Zero Order Reaction
Time in which half of initial amount is left.
[A]o  [A]o/2
[A]o/2
t = o t = t1/2

k = 
t1/2 = 
Thus, for a Zero order reaction, half-life is directly proportional to the initial concentration of the reactant.
Clearly, zero-order reactions are those, whose rates are not affected by change in concentrations of reactants (i.e., independent of concentration). The rates of such reactions only depend upon temperature. Most of photochemical reactions are zero order reactions. Other examples are : decomposition of HI over the surface of gold and NH3 over tungsten.
Example :
(1) Photochemical Reactions, Photosynthesis
(2) CH4 Cl2
Cl - Cl  Cl
Cl
CH4 + Cl  CH3Cl + H
CH3Cl + H
(ii) First Order Reaction
A  product
product
t = o [A]o -
t = t [A] [P]




ln [A]o/[A] = kt

Half life (t1/2) of First Order Reaction
t = t1/2 [A] = [A]o/2
 =
= 




[A] =  where , n = number of half lifes.
where , n = number of half lifes.
Average life

Features of a First Order Reaction
- A first order reaction must follow above form of rate law for all time instants. This means if we are given value of A0 and values of x at different time instants [i.e.(A0 - x) as value of reactants after t], the values of k can be calculated for different time instants by using the above first order law.
If the reaction for which the data were given is a first order reaction, then all values of k will approximately equal to each other. - The time for half reaction for a first order reaction is independent of initial concentration of reactants.
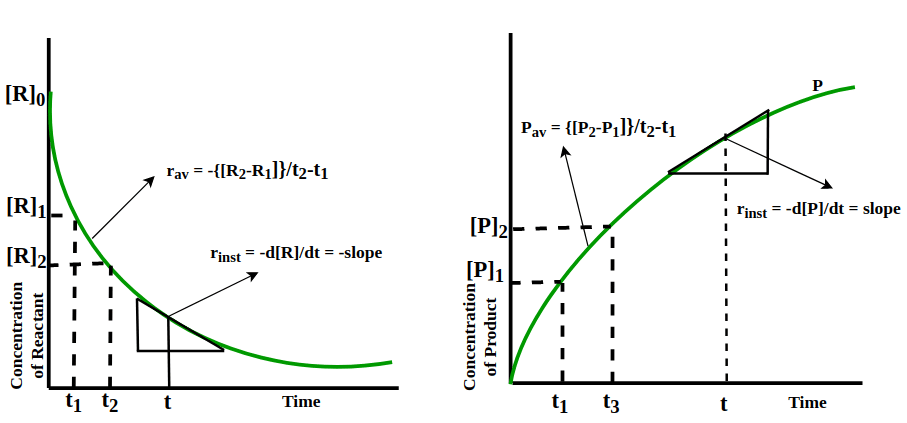
- The concentration of reactants in a first order reaction decreases exponentially with time (see figure)
Note that plot of log10 A vs t is linear.
Example :
- Radioactive disintegration.
- PCl5(g) -> PCl3(g) Cl2(g)
- H2O2 → H2O + 1/2O2
- NH4NO2 → N2 +2H2O
Rate constant of a first order reaction can also be calculated by measuring the concentration of the reactants at two time instants (if the initial concentration is not known).
If A1 and A2 are the reactant's concentrations at two time instants 't1' and 't2' respectively, then we have :
 ...(iii)
...(iii)
and  ... (iv)
... (iv)
Subtracting (iv) from (iii), we get :

Thus, k can be evaluated.
Example: For a reaction 2NO(g) + 2H2(g) → N2(g) + 2H2O (g) ; the following data were obtained.
| [NO] (mol/L) | [H2](mol/L) | Rate (mol/L/s) |
1. | 5 X 10-3 | 2.5 X 10-3 | 3 X 10-5 |
2. | 15 X 10-3 | 2.5 X 10-3 | 9 X 10-5 |
3. | 15 X 10-3 | 10 X 10-3 | 3.6 X 10-4 |
(a) Calculate the order of reaction.
(b) Find the rate constant.
(c) Find the initial rate if [NO] = [H2] = 8.0 x 10-3 M
Sol: Assuming rate law can be expressed as follows :
rate = k[NO]x [H2]y
By analyzing the data :
From observation 1 and 2, we see that [H2] is constant and when [NO] is tripled, the rate is also tripled.
⇒ rate (r) ∝ [NO] ⇒ x = 1
From observations 2 and 3, we see that [NO] is constant; when [H2] is increased four times, the rate also increases four times :
rate ∝ [H2] ⇒ y = 1
⇒ r = k [NO] [H2O]
⇒ The order of reaction w.r.t No and H2 is 1 and the overall order of reaction is 1 1 = 2.
Initial rate = k[NO][H2] = 2.4 x (8 x 10-3)2 = 1.536 x 10-4 mol/L/s.
(iii) Second Order Reaction
Case I:


-  = k[A]2
= k[A]2


k = 
Half-life (t1/2) of Second-Order Reaction
[A]t =  , k = 2/[A]o - 1/[A]o
, k = 2/[A]o - 1/[A]o

t1/2 =
Example:
- Alkaline hydrolysis of esters.
- Self Cannizzaro's reactions.
Case II:

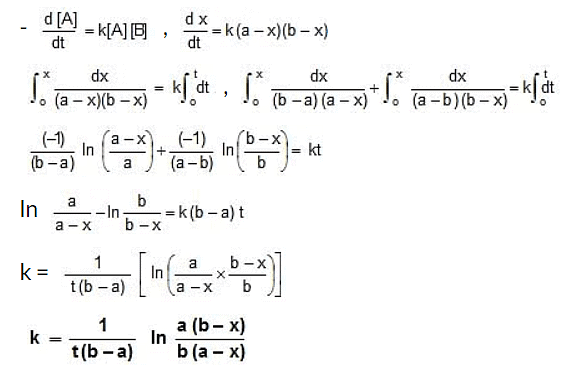
|
100 videos|282 docs|123 tests
|
FAQs on Rate Law and Integrated Rate Equations - Chemistry Class 12 - NEET
| 1. What is the Rate of a Reaction? |  |
| 2. What is Rate Law? |  |
| 3. What is Order of a Reaction? |  |
| 4. What is Molecularity of a Reaction? |  |
| 5. What are Integrated Rate Equations? |  |

|
Explore Courses for NEET exam
|

|



















