Analysis and Testing of Three Phase Transformers
(Refer Slide Time: 01:04)
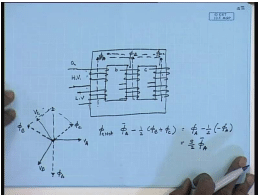
We have seen that in a three phase core type transformer, both the high and the low voltage windings are wound on the same core. The arrangement is somewhat like this. This is the transformer core. I am drawing a 3 core type arrangement – 3 limbed type arrangement rather. The high voltage and the low voltage windings… Let us say this is the HV winding; this is the LV winding of a particular phase; similarly, for the other phases. The individual windings may be connected star-delta or zigzag or whatever.
However, in steady state, with balanced sinusoidal supply, each of this set of windings operate independently of each other. This can be understood as follows. For example, let us say this is phase a winding; this is phase b winding; this is phase c winding. Irrespective of the connections of the individual windings with balanced 3 phase voltage applied between lines, the winding voltages will also be balanced. And we will have the same phase sequence as the line voltage.
So, let us say the high voltage winding is excited. In this particular case, this is the high voltage winding voltage V A phasor; this is V B phasor;and this is V C phasor. Assuming ideal transformer, the flux produced by the high voltage winding is phi A; phase b is phi B;and phase c is phi C which lags the respective applied voltage by 90 degree. So, this is phi A, this is phi B, and this is phi C.
Now, each of these voltages will divide in two equal parts assuming negligible reluctance of the core. One will flow through this – one part; the other part will flow through this; similarly, for the other phases. So, the next flux flowing through limb a is phi A minus half of phi B plus phi C. However, from this phasor diagram, we see that, phi B plus phi C is nothing but minus phi A, because these fluxes are also balanced. So, this is equal to phi A minus half of minus phi A; this is equal to 3 by 2 times phi A. So, phi A net.
Therefore, the net flux linking the HV and LV winding on each phase leg is in phase with the flux produced by that particular winding; it is in fact, proportional. Therefore, with balanced 3 phase supply voltage, each of these phases operate independent of each other; that is, each set of HV and LV winding can be treated separately irrespective of their connections provided we know what are the applied voltages and the currents. That being the case, it is possible at least to do steady state analysis with balanced supply with the 3 phase transformer on per phase basis; that is, given a transformer, we will find out first what are the applied winding voltages and winding currents; and then, proceed in the same manner as that of a single phase transformer. For example, let us take this as an example.
(Refer Slide Time: 07:07)
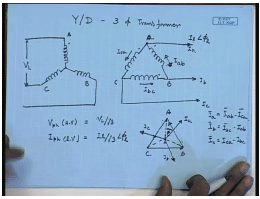
Let us say we have a Y, D-connected 3 phase transformer. This is supplying... So, Y, Dconnected 3 phase transformer... This is the high voltage side connection. And this is A; this is B; this is C. This is the low voltage side – B, A, C. Suppose the applied line to line voltage on the high voltage side is V L and the load current on the low voltage side is I l at an angle phi l. Now, it should be understood that, when the phase angle of the load current is specified, it is with respect to the line phase angle of the line current with respect to line to neutral voltage, not line to line voltage.
So, if we want to convert it into per phase equivalent circuit, then what is the applied phase voltage on the HV side – V phase on the HV side? This is equal to V L by root 3. Similarly, what is the line current through the LV side, phase current through the LV side? I phase – lv; magnitude is I l by root 3. What about the phase angle? For that, let us see the LV side voltage phasor... Line to line voltage phasor diagrams are like this. This is line current I a; this is I b; this is I c. So, this is winding current; this is winding current; this is winding current – I a b, I b c, I c a.
Now, as I said, the line to neutral voltages are these. This is the neutral point. So, this I l let us say is at a lagging angle of phi l. This is say I a; similarly, this will be I b this will be I c. So, what will be the winding currents let us see. So, line current I a can be written as I a b minus I c a. Similarly, I b can be written as line current I b equal to I b c minus I a b;and I c can be written as I c a minus I b c. If we draw the phasor diagram, we see that, this is line current I a; this can be drawn as I a b minus I c a. So, the angle between... If the line voltage A B leads the line to neutral voltage V a by 30 degree; then, line current I a b – angle between line current I a b and voltage V a b will be same as the angle phi l. This can be shown. So, the LV side line current, LV side winding current is also at an angle of phi l. With this, now, it is easy to draw the equivalence circuit of the transformer, because with the winding voltage and the winding currents specified, this set of windings can be treated as a single phase 2 winding transformer. And we already know the equivalent circuit for that.
(Refer Slide Time: 13:54)
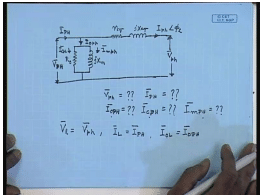
The approximate equivalent circuit will be... This is applied voltage V phase per phase core loss component or core loss resistance. This is per phase magnetizing reactance, per phase equivalent series resistance, per phase equivalent leakage reactance. And the current here is... This is the low voltage side phase voltage V p. This is high voltage side phase voltage V phase; this is low voltage side phase voltage V phase. And the current I phase is at an angle phi l. Hence, following the same procedure as we have used for single phase transformer, we can find out what will be the voltage V phase; what will be the input line current I phase; what will be per phase magnetisation, per phase no-load current I 0 phase, magnetic current and core loss current. All these in per phase basis will be able to find out following the same method as that in a single phase transformer.
Once we have them, then we go back to the original connection of the transformer. We know that, the low voltage side is delta-connected. So, the low voltage side line voltage will be same as the phase voltage. So, low voltage side line voltage will be same as the phase voltage. However, low voltage side line current is not same. On the high voltage side, we have seen that, the high voltage side is star-connected. So, high voltage side line current I L will be same as I phase and all other. The line quantities... So, no-load current will be same as referred to the high voltage side; it will be same as the phase current and also these two components.
So, this is how a 3 phase transformer can be analysed on per phase basis using the same per phase equivalent circuit as that of a single phase transformer. Now, we have seen with single phase transformer. In order to analyse the transformer using this equivalent circuit, we need to know the parameters of the equivalent circuit. And in order to find these parameters, we performed no-load and short circuit test.
(Refer Slide Time: 18:40)
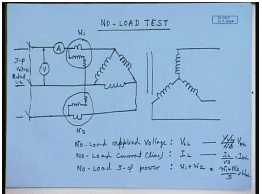
The similar tests are to be carried out for 3 phase transformer as well. So, for a 3 phase transformer, how the no-load circuit will look like? For the same transformer, let us say the no-load test is usually done on the low voltage side. And in this case, the low voltage side is delta-connected. So, you have this delta-connected transformer – delta-connected low voltage side. The high voltage side is star-connected and kept open. This is kept open. Voltage is applied to the low voltage side. In order to measure the line current, an ammeter is connected and also a wattmeter. And here apply rated 3 phase voltage – rated low voltage side 3 phase voltage maybe through a variac. Rated line to line 3 phase voltage is applied here. There are two... The power is measured using 2 wattmeter method. And the line voltage is also measured.
So, as in the case of a single phase transformer, the no-load test will yield three leadings: no-load voltage – this will be line to line voltage V L L; no-load current I L;and the noload power – no-load 3 phase power. This will be given by for 2 wattmeter method. It is reading of W 1 plus W 2. Now, depending on the transformer connection, this is deltaconnected. Therefore, no-load applied phase voltage is V L L by root 3; no load phase current... The phase voltage is same as V L L; this is same as phase voltage. Phase current is I L by root 3. This is equal to I phase – no-load phase or winding current. And the no-load power is – phase power is W 1 plus W 2 by 3. This is equal to W phase. So, once we have converted this no load test data to phase quantities, then this can be used in a similar manner as that in a single phase transformer to find out the shunt branch component of the per phase equivalent circuit, that is, R 0 and X m.
(Refer Slide Time: 23:31)
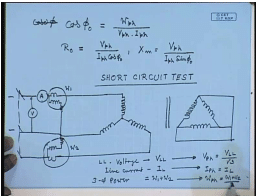
The procedure as we have seen is that, the no-load power factor cos phi 0 equal to noload power per phase divided by no-load phase or winding voltage multiplied by no-load phase current. Once we know cos phi, then we know the R m or R 0 equal to V phase divided by I 0 or I phase cos phi 0 and X m equal to V phase divided by I phase into sine phi 0. So, this gives the shunt branch component of the per phase equivalent circuit of a 3 phase transformer.
In order to find the series branch parameters, that is, R e q and j X e q, we will have to carry out the short circuit test. Short circuit test is done on the high voltage side. Therefore, it is the high voltage side that will be connected and the low voltage side will be short circuited. Low voltage side will be short circuited. The high voltage will be connected through again two wattmeters and an ammeter. This will be supplied from what we call a 3 phase variac in order to control the current flowing into the line. Here again... And a voltmeter will measure the line to line voltage.
Here again the readings that will be taken are line to line voltage. The variac will be adjusted such that, rated line current flows through the high voltage side; then, we will measure line to line voltage; should be V L L. The line current I L and 3 phase power equal to W 1 plus W 2. This we will convert to phase values again. This is starconnected. So, V phase will be equal to V L L by root 3 star-connected. Therefore, I phase is same as I line and per phase power W phase equal to W 1 plus W 2 by 3.
(Refer Slide Time: 29:26)

Once we know the phase voltage current and power, then we proceed in the same manner as that of a single phase transformer to find out the per phase equivalent circuit parameter; that is, Z e q is obtained as V phase by I phase. R e q is obtained as W phase divided by I phasors square. And X e q is obtained as square root of Z e q square minus R e q square. However, it should be appreciated that, the values of R e q, Z e q, R e q, X e q obtained like this refers to the high voltage side. Whereas, the shunt branch parameter that were determined from the no-load test are referred to the low voltage side.
Now, all the parameters have to be transferred to either high voltage side or low voltage side depending on the analysis requirement. For example, the series branch parameter can be converted to the low voltage side by the following relationship; that is, Z e q dash referred to the LV side will be equal to N L V by N H V square into Z e q. R e q dash will be equal to N L V by N H V square into R e q. X e q dash will be equal to N L V by N H V square X e q. Alternately, all the parameters may be expressed in per unit form with the basis selected as – the power base to be selected as the 3 phase power rating of the transformer. And the voltage basis from either side can be selected as the rated line to line voltage of the high voltage side and the low voltage side respectively.
If you do that, then the parameters that we obtain can be used without further referring by turns ratio. In fact, the test data in themselves are sometimes specified in per unit terms; that is, when you are doing no-load test, you can say that, we applied 1 per unit line to line voltage. So, the line current was so many per units and the 3 phase power was so many per units. It can be easily shown that, if the test data themselves are specified in per unit form, then the parameters that we will determine from the test data will also be in per unit. And in which case, again this converting to or referring to different sides will not be necessary. So, let us explain or try to solve a problem to show how a 3 phase transformer can be tested and analysed.
(Refer Slide Time: 33:56)

Let us see; let us take an example. We have an 11 KV by 400 volt, 150 KVA, 50 hertz delta, y-connected 3 phase transformer. From the no-load test data, which was done on the LV side, that is, on the y-connected side is as follows. The line current is 10 ampere and the 3-phase power is 2 kilowatt when rated applied line to line voltage is given. A line to line voltage is rated line to line voltage 400 volts. Similarly, the short circuit test data, which is conducted from the HV side is as follows. The applied line to line voltage is 600 volts. This is again line to line voltage. The HV side here is delta-connected. The line current is measured; the line current is 8 ampere.
And, 3 phase power – this is 3.5 kilowatt. So, let us try to find out the equivalent circuit parameter of this transformer. So, no-load test is performed on the low voltage side, which is star-connected. So, phase voltage is – this is equal to 400 by root 3 equal to 230.9 volts. And line phase current equal to line current equal to 10 amperes. The noload power factor cos phi 0 is given by no-load power – 3 phase power divided by root 3 – no-load voltage – line voltage into line current – comes to be 0.289. Therefore, phi 0 comes to be approximately equal to 73.2 degrees.
(Refer Slide Time: 38:30)

With this, so let us find out R 0. So, this will be referred to LV side. This is found as V phase divided by I phase cos phi 0; that is, 230.9 divided by 10 into 0.289. This comes to 79.91 ohm. X m per phase referred to LV side – X m referred to LV side – V phase divided by I phase sine phi 0. This comes to 24.12 ohm. So, the shunt branch parameters referred to the LV sides are found this way.
Let us now try to find out the series branch parameter from the short circuit test. This is referred to HV side. And HV side is delta-connected. So, HV side phase voltage – SC test – from short circuit test, equal to V L L equal to 600 volts. HV phase current equal to I P H equal to I L by root 3; that is, 8 by root 3. This is equal to 4.62 amperes. Therefore Z e q referred to the HV side equal to V phase divided by I phase equal to 129.9 ohm. R e q referred to HV side equal to 3 phase per phase power. So, 3 phase power is 3.5 into 10 to the power 3 divided by 3 into – this is 3 phase power – into 8 by root 3 square; that is, 3.5 into 10 to the power 3 divided by 8 square equal to – this comes to 54.69 ohm. X e q – HV side equal to square root Z e q square minus R e q square equal to – this comes to 117.83 ohm. Now, these are referred to HV side. However, the R 0 and X m were referred to LV side.
(Refer Slide Time: 44:23)
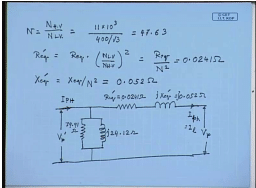
Now, converting the R e q and X e q referred to the LV side; for that, we need to know the turns ratio N H V by N L V. This is equal to... HV side is delta-connected. So, phase voltage and line voltage are same. So, this is 11 KV. LV side is star-connected. So, the phase voltage is 400 by root 3. This comes to 47.63. Therefore, R e q dash equal to R e q into N L V by N H V square equal to R e q divided by N square. This comes to 0.0241 ohm.
Similarly, X e q dash comes to X e q by N square. This comes to 0.052 ohm. Therefore, the per phase equivalent circuit referred to LV side, which is star-connected will look like this. This is the applied voltage V p dash; this is R 0 – the value is... This value is 79.91 ohm. This is j 24.12 ohm. This is R e q dash equal to 0.0241 ohm. This is X e q dash is equal to 0.052 ohm. This is where the secondary phase voltage, the secondary line current; which is same as secondary phase current, because secondary side is deltaconnected;and secondary line current, because secondary side is star-connected; low voltage side is star-connected here. This is the high voltage side phase current – I phase.
(Refer Slide Time: 49:06)

Now, given a load condition, this problem can be now analysed. Let us see a particular example. Let us say that this transformer is connected on the LV side to a balanced load that draws full load current on LV side. It is connected to a balanced load with source; that is, on the LV side, I l equal to full load current at a power factor of 0.85 lagging. On the HV side, let us assume that, it is connected to an 11 KV, 50 hertz source.
Now, let us try to find out the line voltage on the LV side under this working condition. Now, from the given data and referring to this equivalent circuit, V p dash is equal to 11 KV divided by... The high voltage side is delta-connected. Therefore, phase voltage is same as line voltage – 47.63 – divided by turns ratio equal to 230.94 volts. On the low voltage side, which is star-connected, full load current is flowing. And low voltage side is star-connected; so line current is same as phase current. So, I p equal to 150 KVA, which is the rated KVA of the transformer divided by root 3 into rated line voltage. This is equal to 216.5 amperes;and cos phi equal to 0.85 giving phi equal to 31.8 degrees.
(Refer Slide Time: 52:05)

Now, as in this case of a single phase transformer, we can draw the phasor diagram. Let us say this is V p and this is I p; then, this is I p R e q dash; this is V p dash; this is V p; this is I p R e q dash; this is I p X e q dash. Now, this angle is delta. Usually, this delta angle in a transformer is very small. Therefore, we can write V p is approximately equal to, is actually equal to V p dash cos delta minus I p into R e q dash cos phi minus X e q dash sine phi. Since delta is approximately equal to 0, cos delta is approximately equal to 1. Therefore, V p equal to – comes to from this formula – about 220.57 volts. And hence, the low volt – LV line voltage equal to root 3 V p equal to 382.054. In a similar manner, one can find out also the no-load current and the input current – phase current I p dash.
Thank you.




































