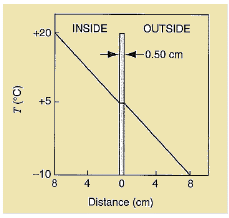
Question 1: An idealized representation of the air temperature as a function of distance from a single-pane window on a calm, winter day is shown in below figure. The window dimensions are 60 cm × 60 cm × 0.50 cm. (a) At what rate does heat flow out through the window? (Hint: The temperature drop across the glass is very small.) (b) Estimate the difference in temperature between the inner and outer glass surfaces.
Concept:-
The rate H at which heat is transferred through the slab is,
(a) directly proportional to the area (A) available.
(b) inversely proportional to the thickness of the slab Δx.
(c) directly proportional to the temperature difference ΔT.
So, H = kA ΔT/ Δx
Here, k is the proportionality constant and is called thermal conductivity of the material.
From the equation H = kA ΔT/ Δx, the temperature difference ΔT will be,
ΔT = H Δx/kA
The temperature gradient is defined as,
Temperature gradient = ΔT/ Δx
Solution:-
(a)To find out the rate of heat flows out through the window, first we have to find out the temperature gradient both inside and outside the window.
Inside, the temperature gradient ΔT/ Δx will be,
ΔT/ Δx = (20° C- 5° C)/8 cm (Since, Δx = 8 cm)
= ((20 +273)K- (5+273) K)/(8 cm×10-2 m/ 1 cm)
= 293 K-278 K/0.08 m
= 187.5 K/m
Rounding off to two significant figures the temperature gradient will be 190 K/m.
Similar result will be occur for also outside.
Area A from which heat will flow from the window will be,
A = (60 cm ×60 cm)2
= [(60 cm×10-2 m/ 1 cm) (60 cm×10-2 m/ 1 cm)]2
= (0.6 m)2
To find out the heat flow H through the air, substitute 0.026 W/m. K for thermal conductivity k, (0.6 m)2 for A and 190 ° C/m for ΔT/ Δx in the equation H = kA ΔT/ Δx,
H = kA ΔT/ Δx
= (0.026 W/m. K) (0.6 m)2 (190 K/m)
= 1.8 W
The value that we arrived at is the rate that heat flows through the air across an area the size of the window on either side of the window. Therefore the rate of heat flows out through the window would be 1.8 W.
(b) To find out the difference in temperature ΔT between the inner and outer glass surfaces, substitute 1.8 W for H, 0.50 cm for Δx, 1.0 W/m. K for k and (0.6 m)2 for A in the equation ΔT = H Δx/kA,
ΔT = H Δx / kA
= (1.8 W) (0.50 cm)/( 1.0 W/m. K)( (0.6 m)2)
= (1.8 W) (0.50 cm×10-2 m/1 cm )/( 1.0 W/m. K)( (0.6 m)2)
= 0.025 K
From the above observation we conclude that, the difference in temperature ΔT between the inner and outer glass surfaces would be 0.025 K.
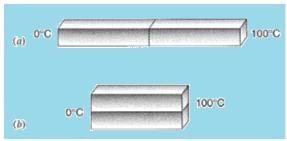
Question 2: Two identical rectangular rods of metal are welded end to end as shown in below figure (a), and 10 J of heat flows through the rods in 2.0 min. How long would it take for 30 J to flow through the rods if they are welded as shown in below figure (b).
Concept:-
The rate H at which heat is transferred through the slab is,
(a) directly proportional to the area (A) available.
(b) inversely proportional to the thickness of the slab Δx.
(c) directly proportional to the temperature difference ΔT.
So, H = kA ΔT/ Δx
Here k is the proportionality constant and is called thermal conductivity of the material.
Solution:-
As the temperature difference in this case ΔT = Thot – Tcold is same for both the case, thus the thermal conductivity will be same for both the cases.
To obtain the rate of heat transfer Ho for the rectangular rod which are connected in series (configuration (a)), substitute 2L for Δx in the equation Ho = kA ΔT/ Δx,
Ho = kA ΔT/ Δx
= kA ΔT/2L
To obtain the rate of heat transfer (Ho)' for the rectangular rod which are connected in parallel (configuration (b)), substitute 2A for A in the equation Ho = kA ΔT/ Δx,
(Ho)' = kA ΔT/ Δx
= k (2A) ΔT/L
So, (Ho)' / Ho = (k (2A) ΔT/L)/ (kA ΔT/2L)
= 4
So, (Ho)' = 4 Ho
Again also rate of heat transfer H is defined as,
H = W/t
Here W is the energy and t is the time.
So, time t will be,
t = W/H
To find the rate of heat transfer Ho for the rectangular rod which are connected in series (configuration (a)), substitute 10 J forW and 2 min for t in the equation t = W/H,
Ho = W/t
= 10 J/ 2 min
= 5 J/min
To find out (Ho)', substitute 5 J/min for Ho in the equation (Ho)' = 4 Ho,
(Ho)' = 4 Ho
= 4(5 J/min)
= 20 J/min
Using equation t = W/H, the time t for 30 J to flow through the rods if they were welded in the figure parallel configuration will be,
t = W/(Ho)'
To obtain the time t for 30 J to flow through the rods if they were welded in the figure parallel configuration, substitute 30 J forW and 20 J/min for (Ho)' in the equation t = W/(Ho)',
t =W/(Ho)'
=(30 J)/(20 J/min)
= 1.5 min
From the above observation we conclude that, the time t for 30 J to flow through the rods if they were welded in the figure parallel configuration would be 1.5 min.
Question 3: Ice has formed on a shallow pond and a steady state has been reached with the air above the ice at -5.2ºC and the bottom of the pond at 3.98ºC. If the total depth of ice + water is 1.42 m, how thick is the ice? (Assume that the thermal conductivities of ice and water are 1.67 and 0.502 W/m.K, respectively.)
Concept:-
The temperature Tx at the interface of a compound slab is equal to (T1R2 + T2 R1) /(R1 + R2).
So, Tx = (T1R2 + T2 R1) /(R1 + R2)
Here, T1, T2 are the temperature of two surfaces (with T2 > T1) and R1, R2 are thermal resistance of the two materials.
Solution:-
At the interface between ice and water Tx = 0° C
Substitute 0° C for Tx in the equation Tx = (T1R2 + T2 R1) /(R1 + R2),
(T1R2 + T2 R1) /(R1 + R2) = Tx
(T1R2 + T2 R1) /(R1 + R2) = 0
So, T1R2 + T2 R1 = 0
Or, k1T1/L1 + k2T2/L2 = 0
(k1T1L2 + k2T2 L1) / L1 L2 = 0
k1T1L2 + k2T2 L1 = 0
k1T1L2 + k2T2 (L-L2) = 0
k1T1L2+ k2T2 L- k2T2 L2 = 0
k2T2 L = k2T2 L2 - k1T1L2
= (k2T2- k1T1) L2
Or, L2 = k2T2 L/(k2T2- k1T1)
Here L is the depth of ice + water and L2 is the depth of ice.
To find out the thickness L2 of ice (depth of ice), substitute 1.67 W/m. K for thermal conductivity of ice k2, -5.20° C for T2, 1.4 m for L, 0.502 W/m . K for thermal conductivity of water k1 and 3.98° C for T1 in the equation L2 = k2T2 L/(k2T2- k1T1),
L2 = k2T2 L/(k2T2- k1T1)
=(1.67 W/m. K) (-5.20° C) (1.4 m) / ((1.67 W/m. K) (-5.20° C) –(0.502 W/m . K) (3.98° C))
=(1.67 W/m. K) (-5.20 +273) K (1.4 m) / ((1.67 W/m. K) (-5.20 + 273) K–(0.502 W/m . K) (3.98 +273) K)
= 635.06 W/(447.23 -139.04) W/m
= 2.06 m
Rounding off to one significant figure, the thickness of the ice will be 2 m.




































