JEE Advanced (Subjective Type Questions): Quadratic Equation & Inequalities (Inequalities) | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Solve for x : 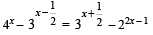 (1978)
(1978)
Ans.
Sol. 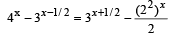
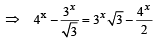
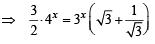
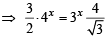
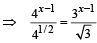
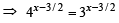
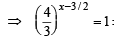
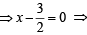 x = 3/2
x = 3/2
Q.2. If (m , n) = 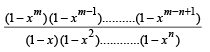 (1978)
(1978)
where m and n are positive integers (n ≤ m), show that (m, n + 1) = (m – 1, n + 1) + xm – n – 1 (m – 1, n).
Ans.
Sol. RHS = (m – 1, n + 1) + xm – n –1 ( m - 1,n)

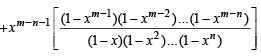
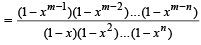
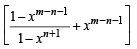
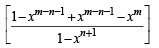
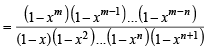
= (m, n +1) = L.H.S. Hence Proved
Q.3. Solve for x :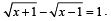 (1978)
(1978)
Ans.
Sol. 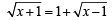
Squaring both sides, we get
x +1 = 1+ x -1+ 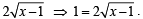
⇒ 1 = 4 (x – 1)
⇒ x = 5/4
Q.4. Solve the following equation for x : (1978)
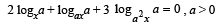
Ans.
Sol. Given a > 0, so we have to consider two cases :
a ≠ 1and a = 1. Also it is clear that x > 0 and x ≠ 1, ax ≠ 1, a2x ≠ 1.
Case I : If a > 0, ≠ 1
then given equation can be simplified as
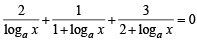
Putting loga x = y, we get
2 (1 + y) (2 + y) + y (2 + y) + 3y (1 + y) = 0
⇒ 6y2 +11y + 4 = 0 ⇒y = -4/3 and-1/2
⇒ loga x =-4 / 3 and logax =-1/2
⇒ x = a -4/3 and x=a-1/2
Case II : If a = 1 then equation becomes
2 logx1 + logx1 + 3 logx1 = 6 logx1 = 0
which is true ∀ x > 0,≠1
Hence solution is if a = 1, x > 0, ≠ 1
if a > 0, ≠ 1 ; x= a-1/2,a-4/3
Q.5. Show that the square of 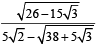 is a rational number. (1978)
is a rational number. (1978)
Ans. Sol.
Let 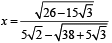
⇒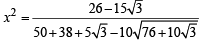
⇒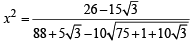
⇒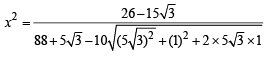
⇒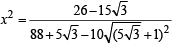
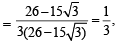 which is a rational number..
which is a rational number..
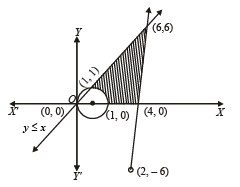
Q.6. Sketch the solution set of the followin g system of inequalities: x2 + y2 – 2x ≥ 0; 3x – y – 12 ≤ 0; y – x ≤ 0; y ≥ 0. (1978)
Ans.
Sol. 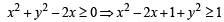
⇒ (x – 1)2 + y2 ≥ 1 which represents the boundary and exterior region of the circle with centre at (1,0) and radius as 1.
For 3x – y ≤ 12, the corresponding equation is 3x – y = 12; any two points on it can be taken as (4, 0), (2, – 6). Also putting (0, 0) in given inequation, we get 0 ≤ 12 which is true.
∴ given inequation represents that half plane region of line 3x – y = 12 which contains origin.
For y ≤ x, the corresponding equation y = x has any two points on it as (0, 0) and (1, 1). Also putting (2, 1) in the given i nequation, we get 1 ≤ 2 wh ich is true, so y ≤ x represents that half plane which contains the points (2, 1). y ≥ 0 represents upper half cartesian plane.
Combining all we find the solution set as the shaded region in the graph.
Q.7. Find all integers x for which (1978)
(5x – 1) < (x + 1)2 < (7x – 3).
Ans.
Sol. There are two parts of this question (5x – 1) < (x + 1)2 and (x + 1)2 < (7x – 3)
Taking first part (5x -1) < (x +1)2 ⇒ 5x -1 < x2 + 2x+1
⇒ x2 - 3x + 2 > 0 ⇒ (x-1)(x - 2)>0
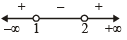 (using wavy method)
(using wavy method)
⇒ x < 1 or x > 2 ....(1)
Taking second part
(x +1)2 < (7x -3) ⇒ x2 - 5x +4< 0
⇒ ( x - 1)(x - 4)<0
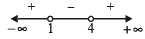 (using wavy method)
(using wavy method)
⇒ 1 < x < 4 ....(2)
Combining (1) and (2) [taking common solution], we get 2 < x < 4 but x is an integer therefore x = 3.
Q.8. If α, β are the roots of x2 + px + q = 0 and γ, δ are the roots of x2 + rx + s = 0, evaluate (α - γ) (α - δ) (β - γ) (β - δ) in terms of p, q, r and s.
Deduce the condition that the equations have a common root.
(1979)
Ans.
Sol. ∵ α, β are the roots of x2 + px + q = 0
∴ α + β = – p, αβ = q
∵ γ,δ are the roots of x2 + rx + s = 0
∴ γ + δ=-r, γδ=s
Now, (α - γ)(α -δ)(β- γ)(β-δ
= [α2 - (γ + δ)α + γδ][β2 - (γ + δ)β + γδ]
= [α2 + rα+ s][β2 + rβ+s]
[∵ α , β are roots of x2 + px + q = 0
∴ α2 + pα + q = 0 and β2 + pβ +q= 0]
= [(r - p)α + (s- q)][(r - p)β + ( s-q)]
= (r - p)2 αβ + (r- p)( s -q)(α + β) + ( s-q)2
= q(r - p)2 - p(r - p)(s -q) + (s-q)2
Now if the equations x2 + px + q = 0 and x2 + rx + s = 0 have a common root say α, then α2 + pα + q = 0 and α2 + rα + s = 0
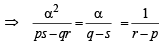
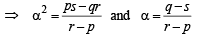
⇒ (q – s )2 = (r – p )(ps – qr) which is the required condition.
Q.9. Given n4 < 10n for a fixed positive integer n ≥ 2, prove that (n + 1)4 < 10n + 1. (1980)
Ans.
Sol. Given that n4 < 10n for a fixed + ve integer n ≥ 2.
To prove that (n + 1)4 < 10n + 1
Proof : Since n4 < 10n ⇒ 10n4 < 10n +1 ....(1)
So it is sufficient to prove that (n + 1)4 < 10n4
Now 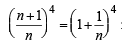
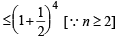
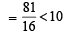
⇒ (n + 1)4 < 10n4 .... (2)
From (1) and (2), (n +1)4 < 10n + 1
Q.10. Let y = 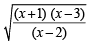 (1980)
(1980)
Find all the real values of x for which y takes real values.
Ans. Sol.
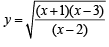
y will take all real values if 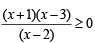
By wavy method
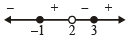
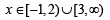
[2 is not included as it makes denominator zero, and hence y an undefined number.]
Q.11. For what values of m, does the system of equations
3x + my = m
2x – 5y = 20
has solution satisfying the conditions x > 0, y > 0. (1980)
Ans. Sol. The given equations are 3x + my – m = 0 and 2x – 5y – 20 = 0 Solving these equations by cross product method, we get
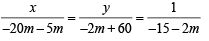 NOTE THIS STEP
NOTE THIS STEP
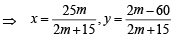
For 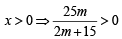 ....(1)
....(1)
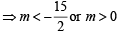
For 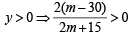 ....(2)
....(2)
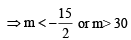
Combining (1) and (2), we get the common values of m as follows :
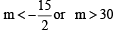
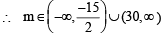
Q.12. Find the solution set of the system (1980)
x + 2y + z = 1;
2x – 3y – w = 2;
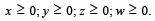
Ans. Sol. The given system is
x + 2y + z = 1 ....(1)
2x - 3y - ω =2 ....(2)
where x, y, z, ω ≥ 0
Multiplying eqn. (1) by 2 and subtracting from (2), we get
7y + 2z + ω = 0 ⇒ ω = - (7 y+ 2z)
Now if y, z > 0, ω < 0 (not possible)
If y = 0, z = 0 then x = 1 and ω = 0 .
∴ The only solution is x = 1, y = 0, z = 0, ω = 0 .
Q.13. Show that the equation esin x –e – sinx – 4 =0 has no real solution. (1982 - 2 Marks)
Ans.
Sol. esin x - e- sinx - 4=0
Let esin x = y then e - sinx = 1/y
∴ Equation becomes,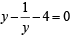
⇒ y2 – 4y – 1 = 0 ⇒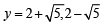
But y is real +ve number,
∴ 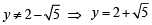
⇒ esin x = 2+ 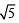 ⇒ sin x = loge (2+
⇒ sin x = loge (2+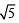 )
)
But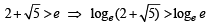
⇒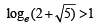 Hence, sin x > 1
Hence, sin x > 1
Which is not possible.
∴ Given equation has no real solution.
Q.14. mn squares of euqal size are arranged to from a rectangle of dimension m by n, where m and n are natural numbers.Two squares will be called ‘neighbours’ if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in its neighbouring squares.
Show that this is possible only if all the numbers used are equal. (1982 - 5 Marks)
Ans. Sol. For any square there can be at most 4, neighbouring squares.
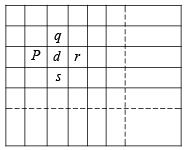
Let for a square having largest number d, p, q, r, s be written then
According to the question, p + q + r + s = 4d
⇒ (d – p) + (d – q) + (d – r) + (d – s) = 0
Sum of four +ve numbers can be zero only if these are zero individually
∴ d – p = 0 = d – q = d – r = d – s
⇒ p = q = r = s = d
⇒ all the numbers written are same.
Hence Proved.
Q.15. If one root of the quadratic equation ax2 + bx + c = 0 is equal to the n-th power of the other, then show that
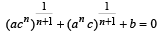 (1983 - 2 Marks)
(1983 - 2 Marks)
Ans. Sol.
Let α, β be the roots of eq. ax2 + bx + c = 0
According to the question, β = an
Also α + β = – b/a ; αβ = c/a
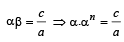
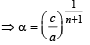
then α + β = – b/a ⇒ 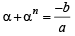
or 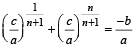
⇒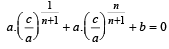
⇒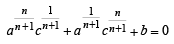
⇒ 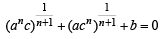
Hence Proved.
Q.16. Find all real values of x which satisfy x2 - 3x + 2 > 0 and x2 - 2 x - 4 ≤ 0 (1983 - 2 Marks)
Ans. Sol. x2 -3x+ 2 >0, x2 -3x- 4 ≤ 0
⇒ (x – 1) (x – 2) > 0 and (x – 4) (x + 1) < 0
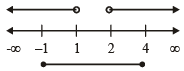
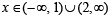 andx ∈ [-1, 4]
andx ∈ [-1, 4]
∴ Common solution is 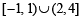
Q.17. Solve for x; 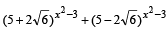 = 10 (1985 - 5 Marks)
= 10 (1985 - 5 Marks)
Ans. Sol. The given equation is
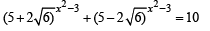 ....(1)
....(1)
Let 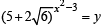 ....(2)
....(2)
then 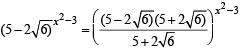
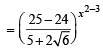
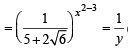 (Using (2))
(Using (2))
∴ The given equation (1) becomes 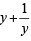 = 10
= 10
⇒ y2 - 10y + 1=0 ⇒ 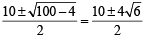
⇒ y = 5 + 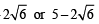
Consider, y = 5+ 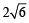
⇒ 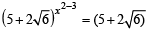
⇒ x2 – 3 = 1 ⇒ x2 = 4 ⇒ x = ± 2
Again consider
y = 5 - 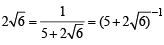
⇒ 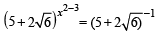 ⇒ x2 – 3 = – 1
⇒ x2 – 3 = – 1
⇒ x2 = 2 ⇒ x = ±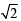
Hence the solutions are 2, – 2, 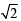 , -
, -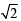
Q.18. For a ≤ 0, determine all r eal roots of the equation x2 - 2a | x - a | - 3a2 = 0 (1986 - 5 Marks)
Ans.
Sol. The given equation is, x2 – 2a | x – a | – 3a2 = 0
Here two cases are possible.
Case I : x – a > 0 then | x – a | = x – a
∴ Eq. becomes x2 – 2a (x – a) – 3a2 = 0
or x2 – 2ax – a2 = 0 ⇒ 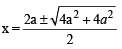
⇒ x = a±a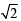
Case II : x – a < 0 then | x – a | = – (x – a)
∴ Eq. becomes
x2 + 2a (x – a) – 3a2 = 0
or x2 + 2ax – 5a2 = 0 ⇒ 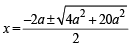
⇒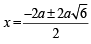 ⇒
⇒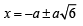
Thus the solution set is 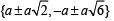
Q.19. Find the set of all x for which 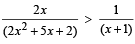 (1987 - 3 Marks)
(1987 - 3 Marks)
Ans. Sol. We are given 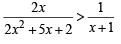
⇒ 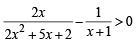
⇒ 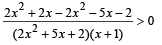
⇒ 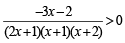
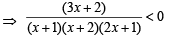
⇒ 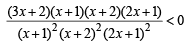
⇒ (3x + 2) (x + 1) (x + 2) (2x + 1) < 0 ....(1)
NOTE THIS STEP
: Critical pts are x = – 2/3, –1, – 2, – 1/2
On number line
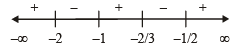
Clearly Inequality (1) holds for,
x ∈(– 2, – 1) ∪ (– 2/3, – 1/2)
[asx ≠ -2, -1, -2 / 3,-1 / 2]
Q.20. Solve | x2 + 4 x + 3 | +2x + 5=0 (1988 - 5 Marks)
Ans. Sol. The Given equation is, | x2 + 4x + 3 | + 2x + 5 = 0 Now there can be two cases.
Case I : x2 + 4x + 3≥0 ⇒ (x +1)(x + 3)≥0 ⇒ x ∈ (-∞, - 3] ∪ [-1,∞) ....(i)
Then given equation becomes,
⇒ x2 + 6x + 8=0
⇒ ( x + 4)(x + 2)= 0 ⇒ x = – 4, – 2
But x = – 2 does not satisfy (i), hence rejected
∴ x = – 4 is the sol.
Case II : x2 + 4x + 3 < 0
⇒ (x + 1) (x + 3) < 0
⇒ x ∈ (– 3, – 1) ....(ii)
Then given equation becomes, – (x2 + 4x + 3) + 2x + 5 = 0
⇒ – x2 – 2x + 2 = 0 ⇒ x2 + 2x – 2 = 0
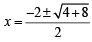 ⇒
⇒ 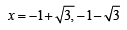
Out of which x = – 1 – 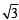 is sol.
is sol.
Combining the two cases we get the solutions of given equation as x = – 4, – 1–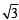
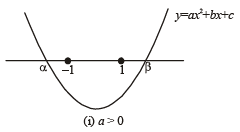
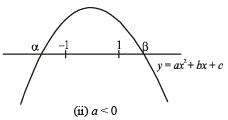
Q.21. Let a, b, c be real. If ax2 + bx + c = 0 has two real roots α and β, where α < -1 and β > 1 , then show that
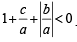 (1995 - 5 Marks)
(1995 - 5 Marks)
Ans. Sol. Given that for a, b, c ∈ R, ax2 + bx + c = 0 has two real roots a and b, where a < – 1 and b > 1. There may be two cases depending upon value of a, as shown below.
In each of cases (i) and (ii) af (–1) < 0 and af (1) < 0
⇒ a (a – b + c) < 0 and a (a + b + c) < 0 Dividing by a2 (> 0), we get
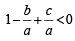 ....(1)
....(1)
and 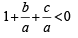 ....(2)
....(2)
Combining (1) and (2) we get
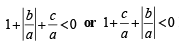 Hence Proved.
Hence Proved.
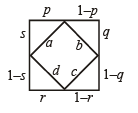
Q.22. Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c, and d denote the lengths of the sides of the quadrilateral, prove that 2 ≤ a2+b2+c2+d2 ≤ 4. (1997 - 5 Marks)
Ans.
Sol. a2 = p2 + s2, b2 = (1– p)2 + q2
c2 = (1– q)2 + (1 – r)2,
d2 = r2 + (1– s)2
∴ a2 + b2 + c2 + d2 = {p2 + (1– p)2}+{q2 – (1– q)2}
+ { r2 + (1– r)2 } +{s2 + (1– s)2 }
where p, q, r, s all vary in the interval [0, 1].
Now consider the function
y2 = x2 + (1– x)2, 0 ≤ x≤ 1,
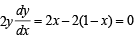
⇒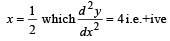
Hence y is minimum at x = 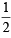 and its minimum
and its minimum
value is 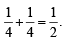
Clearly value is maximum at the end pts which is 1.
∴ Minimum value of a2 + b2 + c2 + d2 = and maximum value is 1 + 1+ 1 + 1= 4. Hence proved.
and maximum value is 1 + 1+ 1 + 1= 4. Hence proved.
Q.23. If α, β are the roots of ax2 + bx + c = 0, ( a ≠ 0 ) and α + δ, β + δ are the roots of Ax2 + Bx + C = 0, ( A ≠ 0) for some constant δ, then prove that 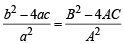 (2000 - 4 Marks)
(2000 - 4 Marks)
Ans. Sol. We know that, (α-β)2 = [(α+δ) - (β +δ)]2
⇒ (a+β)2 - 4αβ = (α +δ+β+δ)2 -4(α+δ)(β +δ)
⇒ 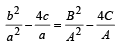
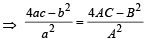
[Here α + β=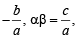
(α+δ) (β +δ)
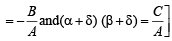
Hence proved.
Q.24. Let a, b, c be real numbers with a ≠ 0 and let α, β be the roots of the equation ax2 + bx + c = 0. Express the roots of a3x2 + abcx + c3 = 0 in terms of α, β. (2001 - 4 Marks)
Ans. Sol. Divide the equation by α3, we get
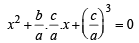
⇒ x2 – (α + β). (αβ) x + (αβ)3 = 0
⇒ x2 – α2βx – αβ2 x + (αβ)3 = 0
⇒ x (x – α2β) – αβ2 (x – α2β) = 0
⇒ (x – α2β) (x – αβ2) = 0
⇒ x = α2 β, αβ2
which is the required answer.
Q.25. If x2 + (a – b) x + (1 – a – b) = 0 where a, b ∈ R then find the values of a for which equation has unequal real roots for all values of b. (2003 - 4 Marks)
Ans. Sol. The given equation is, x2 + (a – b) x + (1– a – b) = 0, a, b ∈ R
For this eqn to have unequal real roots ∀ b D > 0
⇒ (a – b)2 – 4 (1– a – b) > 0
⇒ a2 + b2 – 2ab – 4 + 4a + 4b > 0
⇒ b2 + b (4 – 2a) + a2 + 4a – 4 > 0
Which is a quadratic expression in b, and it will be true ∀ b∈R if discriminant of above eqn less than zero.
i.e., ( 4 –2a)2 – 4 (a2 + 4a – 4) < 0
⇒ (2 – a)2 – (a2 + 4a – 4) < 0
⇒ 4 – 4a + a2 – a2 – 4a + a < 0
⇒ – 8a + 8 < 0
⇒ a > 1
Q.26. If a, b, c are positive real numbers. Then prove that (a + 1)7 (b + 1)7 (c + 1)7>77 a4b4c4 (2004 - 4 Marks)
Ans. Sol. Given that a, b, c are positive real numbers. To prove that (a + 1)7 (b + 1)7 (c + 1)7 > 7 7 a4b4c4
Consider L.H.S. = (1+ a)7. (1+ b)7. (1+ c)7
= [(1 + a) (1+ b) (1+ c)]7[1 + a + b + c + ab + bc + ca + abc]7
> [a + b + c + ab + bc + ca + abc]7 ....(1)
Now we know that AM ≥ GM using it for +ve no’s a, b, c, ab, bc, ca and abc, we get
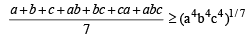
⇒ (a + b + c + ab + bc + ca+ abc)7 ≥ 77 (a4b4c4)a
From (1) and (2),
we get [(1 + a) (1 + b) ( 1 + c)]7 > 77a4 b4 c4
Hence Proved.
Q.27. Let a and b be the roots of the equation x2 – 10cx – 11d = 0 and those of x2 – 10ax – 11b = 0 are c, d then the value of a + b + c + d, when a ≠ b ≠ c ≠ d, is. (2006 - 6M)
Ans. Sol. Roots of x2 – 10cx – 11d = 0 are a and b ⇒ a + b = 10c and ab = – 11d
Similarly c and d are the roots of x2 – 10ax – 11b = 0
⇒ c + d = 10a and cd = – 11b
⇒ a + b + c + d = 10 (a + c) and abcd = 121 bd
⇒ b + d = 9(a + c) and ac = 121
Also we have a2 – 10 ac – 11d = 0 and c2 – 10ac – 11b = 0
⇒ a2 + c2 – 20ac – 11 (b + d) = 0
⇒ (a + c)2 – 22 × 121 – 99 (a + c) = 0
⇒ a + c = 121 or – 22 For a + c = – 22,
we get a = c
∴ rejecting this value we have a + c = 121
∴ a + b + c + d =10 (a + c) = 1210
|
446 docs|929 tests
|





















