JEE Advanced (Subjective Type Questions): Mathematical Induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q. 1. Given that (1979) C₁ + ²C₂x + ³C₃x² + .............. + 2n C_2nx^{2n – 1} = 2n (1 + x)^{2n – 1}

where Cr = 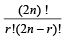                                  r = 0, 1, 2, .................., 2n

Prove that

C₁² – 2C₂² + 3C₃² – ...................... – 2nC_2n² = (– 1)ⁿn C_n.

Ans. Sol.  Given that

C₁ + 2C₂x + 3C₃x² +....+ 2nC_2nx^{2n – 1} = 2n (1 + x)^2n–1    ....(1)

where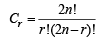  

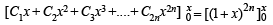
⇒ C₁x + C₂x² + C₃x³ +....+ C_2nx²ⁿ = (1+ x)^{2n – 1} 
⇒ C₀ + C₁x + C₂x² + C₃x³ + ....+ C_2nx²ⁿ = (1+ x)²ⁿ ....(2)

Changing x by 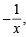   we get

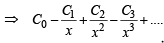
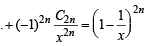
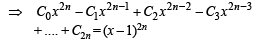....(3)

Multiplying eqn. (1) and (3) and equating the coefficients of x^2n–1 on both sides, we get

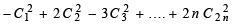
= coeff.of x^{2 n-1} in 2n( x - 1) (x²- 1)^2n-1 

= 2n [coeff. of  x^2n–2 in (x²–1) ^2n–1 – coeff. of x^2n–1 in (x²–1)^2n–1]

⇒ 

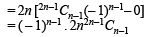
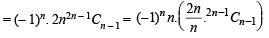
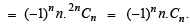 (∵ ²ⁿC_n= C_n)

Hence Proved.

Q.2. Prove that 7²ⁿ + (2^{3n – 3})(3^{n – 1}) is divisible by 25 for any natural number n. (1982 - 5 Marks)

Ans. 

Sol.  P(n) : 7²ⁿ + 2^{3n –3}, 3^n–1 is divisible by 25 ∀n∈N .
Let us prove it by Mathematical Induction :
P(1) : 7² + 2⁰.3⁰ = 49 + 1= 50 which is divisible by 25.
∴ P (1) is true.
Let P(k) be true that is 7^2k  +2^3k–3, 3^k–1 is divisible by 25.
⇒ 7^2k + 2^3k–3. 3^k–1 = 25m where  m ∈Z .
⇒ 2^{3k – 3} . 3^k–1 = 25m – 72k ....(1)
Consider P(k + 1) : 7^{2(k + 1)} + 2^{3(k + 1)} –3 .3^{k + 1 – 1} 
= 7^2k .7² + 2^3k. 3^k = 49. 7^2k + 2³ . 3.2^3k–3 . 3^k–1 
= 49. 7^2k + 24 ( 25m – 7^2k) (Using IH eq. (1))
= 49. 7^2k + 24 × 25m – 24 × 7^2k 
= 25. 7^2k + 24 × 25m = 25 (7^2k + 24 m)
= 25 × some integral value which is divisible by 25.
∴ P(k + 1) is also true.
Hence by the principle of mathematical induction
P(n) is true ∀ n∈Z .

Q.3. If (1 + x)ⁿ = C₀ + C₁x + C₂x² + ...... + C_nxⁿ then show that the sum of the products of the C_i'^s taken two at a time,represented by 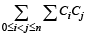  is  equal to 

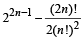           (1983 - 3 Marks)

Ans. 

Sol.  S = ∑∑ C_iC_j 
0 ≤ i < j≤n NOTE THIS STEP

⇒ S = C₀ (C₁ + C₂ + C₃ +....+ C_n) + C₁ (C₂ + C₃ +....+ C_n) + C₂ (C₃ + C₄ + C₅ +.... C_n) +.... C_n–1(C_n)

⇒ S = C₀ (2ⁿ – C₀) + C₁ (2ⁿ – C₀ – C₁) + C₂(2ⁿ – C₀– C₁– C₂) + ....+ C_{n – 1}(2ⁿ – C₀ – C₁....C_{n – 1)} + C_n (2ⁿ – C₀– C₁.... C_n)

⇒ S = 2ⁿ (C₀ + C₁ + C₂ +....+ C_{n – 1} + C_n)

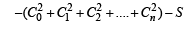
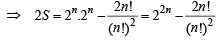
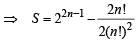
Q.4. Use mathematical Induction to prove : If n is an y odd positive integer, then n(n² – 1) is divisible by 24. (1983 - 2 Marks)

Ans. Sol.  P(n) : n (n²–1) is divisible by 24 for n odd +ve integer.

For n = 2m –1, it can be restated as P(m) : (2m – 1) (4m² – 4m) =  4m (m – 1) (2m – 1) is divisible by 24 ∀ m ∈ N

⇒ P(m) : m (m – 1) (2m – 1) is divisible by 6 ∀ m ∈N .

Here P(1) = 0, divisible by 6.
∴ P(1) is true.

Let  it be true for m = k, i.e.,
k (k–1) (2k–1) = 6p
⇒ 2 k³ – 3k² + k = 6p                ...(1)

Consider P(k + 1) : k (k + 1) (2k + 1) =2k³ + 3k² + k
= 6p + 3k² + 3k² (Using (1)
= 6 (p + k²)
⇒ divisible by 6
∴ P (k + 1) is also true.
Hence P(m) is true ∀ m ∈N .

Q.5. If p be a natural number then prove that p^{n + 1} + (p + 1)^{2n – 1} is divisible by p² + p + 1 for every positive integer n. (1984 - 4 Marks)

Ans. Sol.  P(n) : P^{n + 1} + (p + 1)^2n–1 is divisible by p² + p + 1
For n = 1, P(1) : p² + p + 1
which is divisible  by p² + p + 1.
∴ P(1) is true.
Let P(k) be true, i.e., p^k+1 + (p + 1)2^k–1 is divisible by p² + p + 1
⇒ p^k+1 + (p + 1)^2k–1 
= (p² + p + 1) m ....(1)
Consider P(k + 1) : p^k+2 + (p + 1)^2k+1
= p . p^k+1 + (p + 1)^2k–1. (p + 1)²
= p [m (p² + p + 1) – (p + 1)^{2k – 1}] + (p + 1)^{2k – 1}(p + 1)² 
= p (p² + p + 1)m – p (p + 1)^{2k – 1} + (p + 1)^{2k – 1}  (p² + 2p + 1)
= p (p² + p + 1)m + (p + 1)^{2k – 1}(p² + p + 1)
= (p² + p + 1) [mp + (p + 1)^{2k – 1}] = (p² + p + 1)
some integral value
∴  divisible by p² + p + 1    
∴ P (k + 1) is also true.
Hence by principle of mathematical induction P(n) is true ∀ n∈N .

Q.6. Given s_n = 1 + q + q² + ...... + qⁿ ;

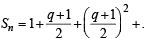
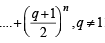Prove that

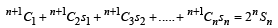          (1984 - 4 Marks)

Ans. Sol.  

We have 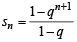 ....(1)

and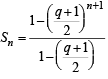  

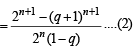
Now,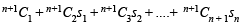  

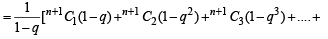
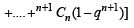 Using (1)

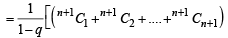
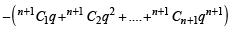
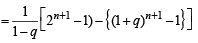
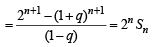[Using eq. (2)] 

Q.7. Use meth od of mathematical induction 2.7ⁿ + 3.5ⁿ – 5 is divisible by 24 for all n > 0 (1985 - 5 Marks)

Ans. 

Sol.  Let A_n =  2.7ⁿ + 3.5ⁿ – 5
Then A₁ = 2.7 + 3.5 – 5 =14 + 15 – 5 = 24.
Hence A₁ is divisible by 24.
Now assume that Am is divisible by 24 so that we may write
A_m = 2.7^m + 3.5^m - 5= 24k , k ∈N ....(1)
Then A_{m + 1} – A_m 
= 2 (7^{m + 1} – 7^m) + 3 (5^{m + 1} – 5^m) – 5 + 5
= 2.7^m(7 – 1)  + 3.5^m (5 – 1) = 12. (7^m + 5^m)
Since 7^m and 5^m are odd integers ∀ m ∈ N , their sum must be an even integer, say 7^m + 5^m = 2p, p ∈ N .
Hence A_m+1– A_m=12.2 p = 24 p
or A_m+1= A_m + 24p = 24k + 24p [by (1)]
Hence A_m+1 is divisible by 24.
It follows by mathematical induction that A_n is divisible by 24 for all  n ∈ N .

Q.8. Prove by mathematical induction that – (1987 - 3 Marks)

 for all positive Integers n.

Ans. Sol.  

Let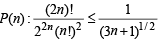 

For n =1,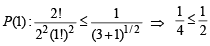  

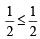⇒    which is true for n =1

Assume that P(k) is true, then

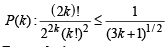     ....(1)

For n = k +1,

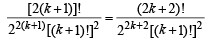
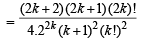
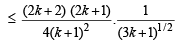
[Using Induction hypothesis (1)]

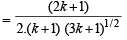
Thus,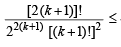 

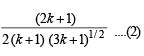
In order to prove P(k + 1), it is sufficient to prove that

....(3)

Squaring eq. (3), we get

⇒ (2k + 1)² (3k + 4) – 4 (k + 1)² (3k + 1) ≤ 0
⇒ (4k² + 4k + 1) (3k + 4) - 4 (k² + 2k +1) (3k +1)≤ 0
⇒ (12k³ + 28k² + 19k + 4) - (12k³ + 28k² + 20k + 4)≤ 0
⇒ – k ≤ 0

which is true.
Hence from (2) and (3), we get

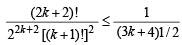
Hence the above inequation is true for n = k +1 and by the principle of induction it is true for all n ∈N .

Q.9. Let R = 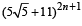  and  f = R – [R], where [  ] denotes the greatest integer function. Prove that Rf = 4²ⁿ⁺⁴ . (1988 - 5 Marks)

Ans. Sol.  We have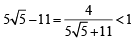  

Therefore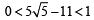  

This gives us 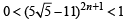 for every positive integer n.

Also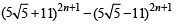 

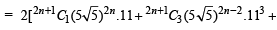
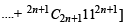
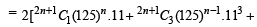
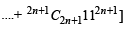
= 2k
....(1)
where k is some positive integer.

Let F 

Then equation (1) becomes R – F = 2k

⇒ [R] + R – [R]– F = 2k ⇒ [R] + f – F = 2k
⇒ f – F = 2k – [R]  ⇒ f – F is an integer..
But 0 ≤ f < 1 and 0 <F<1
Therefore –1 < f – F < 1
Since f – F is an integer, we must have  f – F = 0
⇒ f  = F.
Now, Rf = RF =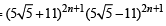

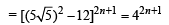
Q.10. Using mathematical induction, prove that(1989 - 3 Marks)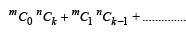 
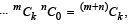 where m, n, k are positive integers, and ^p C_q = 0 for p < q.

Ans. 

Sol.  Let the given statement be

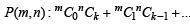
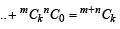
where m, n, k ∈ N and ^pC_q = 0 for p<q.

As k is a positive integer and ^p Cq = 0 for p<q .
∴ k must be a positive integer less than or equal to the smaller of m and n,

We have  k = 1, when m = n = 1

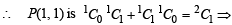1 + 1= 2.

Thus P (1, 1) is true.
Now let us assume that P(m, n) holds good for any fixed value of  m and  n  i.e.

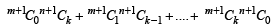
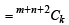....(2)

Consider LHS

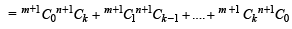
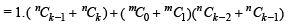
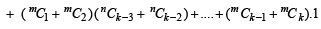
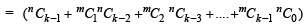
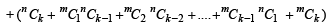
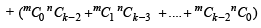
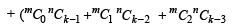
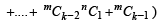
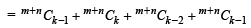[Using (1)]

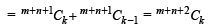
Hence the theorem holds for the next integers  m + 1 and n +1. Then by mathematical induction the statement P (m, n) holds for all positive integral values of m and n.

Q.11. Prove that

C₀ - 2²C₁ + 3²C₂ - ............ + ( -1)ⁿ (n+ 1)²C_n = 0, n > 2, where C_r = ⁿC_r .

Ans. Sol.  We know that (1 – x)ⁿ  =  C₀ – C₁x + C₂x² – C₃x³ +....+ (– 1)ⁿ C_nxⁿ 
Multiplying both sides by x, we get
x(1 – x)ⁿ  = C₀ x – C₁x² + C₂x³ – C₃x⁴ +....+ (– 1)ⁿ C_nxⁿ⁺¹
Differentiating both sides w.r. to x, we get
(1 – x)ⁿ – nx (1 – x)ⁿ – 1 = C₀ – 2C₁ x + 3C₂ x² – 4C₃x³ +....+ (– 1)ⁿ (n + 1) C_nxⁿ 
Again multiplying both sides by x, we get
x (1 – x)ⁿ – nx² (1 – x)n – 1 = C₀x – 2C₁x² + 3C₂x³ – 4C₃x⁴ +....+ (– 1)ⁿ (n + 1) C_nx^{n + 1}
Differentiating above with respect to x, we get
(1 – x)ⁿ – nx (1– x)^{n – 1}– 2nx (1– x)^{n – 1} + nx²  (n – 1) (1 – x)^{n – 2} 
= C₀ – 2² C₁ x + 32 C₂ x² – 4² C₃ x³+....+  ( – 1)ⁿ (n + 1)² C_n xⁿ 
Substituting x = 1, in above, we get
0 = C₀ – 2²C₁+ 3²C₂– 4²C₃ +....+ ( – 1)ⁿ (n + 1)²C_n
Hence Proved.

Q.12. Prove that 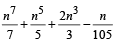 is an integer for every positive integer n. (1990 -  2 Marks)

Ans. Sol.   We have

P(n) : 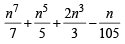is an integer, ∀ n∈N

P(1) : 

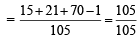 = 1 an integer

∴ P(1) is true
Let P(k) be true i.e.

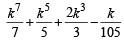is an integer

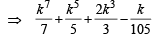 = m, (say)

m ∈N                          ....(1)
Consider P(k + 1) :

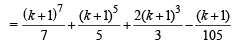
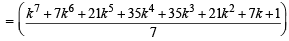
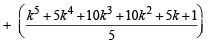
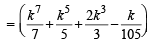
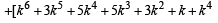
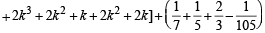
= m + some integral value + 1
=  some integral value
∴ P (k + 1) is also true.
Hence P (n) is true ∀ n ∈N , (by the Principle of Mathematical Induction.)

Q.13. Using in duction or otherwise, prove that for any nonnegative integers m, n, r and k, (1991 -  4 Marks)

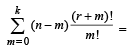
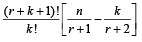
Ans. Sol.  Let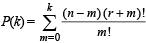   

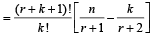
For k = 1, we will have two terms, on LHS, in sigma for m = 0 and m = 1, so that

LHS  =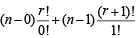 

and  RSH =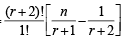

Hence LHS = RHS for k = 1.
Now let the formula holds for k = s, that is let

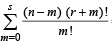
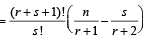 ...(1)

Let us add next term corresponding to  m = s + 1 i.e.

adding 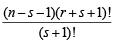to  both sides, we get

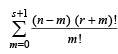
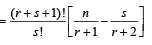
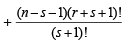
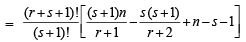
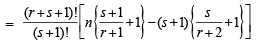
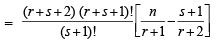
Hence the formula holds for k = s + 1 and so by the induction principle, the formula holds for all natural numbers k.

Q.14. If 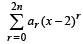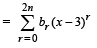and ak = 1 for all k ≥ n, then show that  b_n = ²ⁿ⁺¹C_n+1 (1992 -  6 Marks)

Ans.

 Sol.  Given that

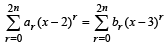....(1)

and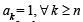 

To prove b_n=²ⁿ⁺¹C_n+1 In the given equation (1) let us put x –3 = y so that x – 2 = y + 1 and we get

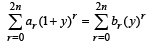
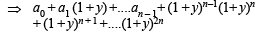
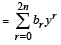[Using a_k = 1, ∀ k≥n]

NOTE THIS STEP :
⇒ ⁿC_n + ^{n + 1}C_n + ^{n + 2} C_n +....+ ²ⁿC_n = b_n
⇒ (^{n + 1}C_{n + 1}+ ^{n +1}C_n) + ^{n + 2}C_n +....+ ²ⁿC_n = b_n
[Using ⁿC_n= ^{n + 1}C_{n + 1}= 1]
⇒ b_n = ^{n + 2}C_{n + 1} + ^{n + 2}C_n +....+ ²ⁿC_n
[Using ^mC_r + ^mC_{r -–1} = ^{m + 1}C_r]
Combining the terms in similar way, we get
⇒ b_n= ²ⁿC_n+1 + ²ⁿC_n ⇒ b_n = ^{2n + 1}C_{n + 1}
Hence Proved

Q.15. Let p ≥ 3 be an integer and α, β be the roots of x² – (p + 1)x + 1 = 0 using mathematical induction show that αⁿ + βⁿ .
 (i) is an integer and (ii) is not divisible by p (1992 -  6 Marks)

Ans. 

Sol.  Since α, β are the roots of  x² – (p + 1) x +1 = 0
∴α + β = p + 1;  αβ = 1
Here p ≥ 3 and p ∈ Z

(i) To prove that αⁿ + βⁿ is an integer.
Let us consider the statement, “αⁿ + βⁿ is an integer.”
Then for n = 1,α + β = p + 1 which is an integer, p being an integer.
∴Statement is true for n = 1
Let the statement be true for n ≤ k, i.e., α^k + β^k is an integer Then ,
α^{k +1} + β^k+1 = α^k . α + β^k.β
= α(α^k +β^k) + β(α^k + β^k) -αβ^k -α ^k β
= (α + β)(α ^k +β^k ) -αβ(α ^{k -1} +β^k-1
= (α +β)(α ^k + β^k) - (α ^{k -1} +β^k-1) .....(1)  [as αβ = 1]
= difference of two integers = some integral value
⇒ Statement is true for n = k + 1.
∴By the principle of mathematical induction the given statement is true for ∀ n∈ N .

(ii) Let R_n be the remainder of αⁿ +βⁿ when divided by p where 0 ≤ R_n ≤p-1
Since α + β = p +1     ∴R₁
= 1 Also α²+ β²= (α + b)² -2αβ = ( p + 1)² -2      
= p² + 2p – 1= p (p + 1) + p – 1
∴R₂ = p –1

Also from equation (1) of previous part
(i), we have αⁿ⁺¹ +βⁿ⁺¹ = ( p + 1) (αⁿ +βⁿ ) - ( α^n-1 + β^n-1)     =
p (αⁿ +βⁿ ) + (αn +βn ) - (α^n-1 +β^n-1)
⇒ R_n+1 is the remainder of R_n – R_n–1 when divided by p
∴We  observe that R₂ – R₁= p – 1–1
∴R₃ = p – 2
Similarly, R₄ is the remainder when R₃ – R₂ is divided by p
where R₃ – R₂ = p – 2 – p + 1 = – 1 = – p + (p – 1)  ∴R₄ = p – 1
R₄ – R₃ = p – 1 – p + 1=1           ∴R₅= 1
R₅ – R₄ = 1– p + 1 = – p + 2               ∴R₆ = p – 2
It is evident for above that the remainder is either 1 or p –1 or p – 2.
Since p ≥ 3, so none is divisible by p.

Q.16. Using mathematical induction, prove that tan ^-1(1/3) + tan ^-1 (1/7) + ..... tan^-1{1 /(n² +n+ 1)} = tan ^-1{n /(n+ 2)} (1993 -  5 Marks)

Ans. Sol.  To prove

P(n) :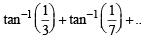 

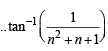
For n = 1,  LHS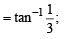 

RHS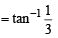 ⇒ LHS  =  RHS.

∴P(1) is true.
Let P(k) be true, i.e.

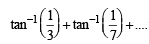
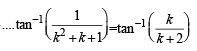
Consider P (k + 1)

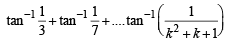
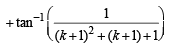
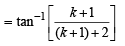
LHS  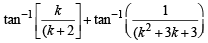=  [Using equation (1)]

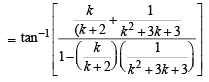
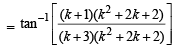
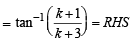
∴P(k  + 1) is also true.
Hence by the principle of mathematical induction P(n) is true for every natural number.

Q. 17. Prove that 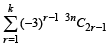 = 0, where k = (3n) /2 and n is an even positive integer. (1993 -  5 Marks)

Ans. Sol.  

To evaluat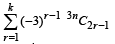e where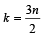

and n is +ve even interger.

Let n = 2m, where m ∈ z⁺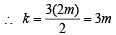

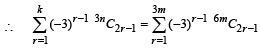
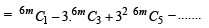...(1)

Now we know that

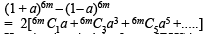...(2)

Keeping in mind the form of RHS in equation (1) and in equation (2)

We put 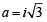 in equation (2) to get

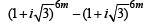
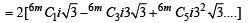
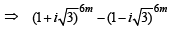
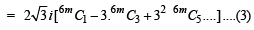
But

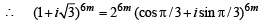
NOTE THIS STEP

 [Using D’ Moivre’s thm.]

Similarly,

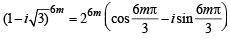
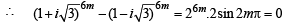
Substituting the above in equation (3) we get

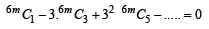
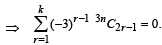
Hence Proved

Q.18. If x is not an integral multiple of 2π use mathematical induction to prove that : (1994 -  4 Marks)

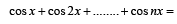
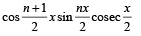
Ans. Sol.  Let  P (n) : cos x + cos 2x +....+ cos nx

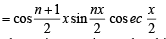....(1)

where x is not an integral multiple of 2 p .
For n = 1 P (1) : L.H.S.  = cos x

R.H.S.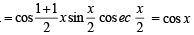

L.H.S. = R.H.S.
⇒ P (1) is true.

Let P(k) be true i.e.
cos x + cos 2x + ....+ cos kx

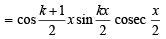....(2)

Consider P(k + 1) :
cos x + cos 2x + ....+ cos kx + cos (k + 1) x

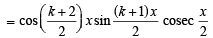
.L.H.S. [cos x + cos 2x + ....+ cos kx + cos (k + 1) x

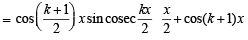[Using (2)]

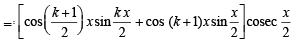
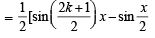
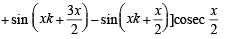
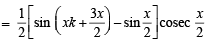
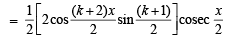= R.H.S.

∴P (k + 1) is also true.
Hence by the principle of mathematical induction
P (n) is true ∀ n∈ N .

Q.19. Let n be a positive integer and (1994 -  5 Marks)
 (1 + x + x²)ⁿ = a₀ + a₁x + ............+ a_2n x²ⁿ 
 Show that a₀² – a₁² + a₂² .............+ a_2n² = a_n

Ans. Sol.  Given that,

(1 + x + x²)ⁿ = a₀ + a₁x +....+ a_2nx²ⁿ ....(1)
where n is a +ve integer.
Replacing x by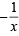in eq n (1), we get

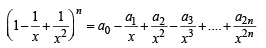....(2)

Multiplying eq.’s (1) and (2) :

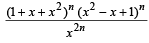
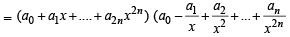
Equating the constant terms on both sides we get

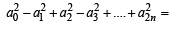constant term in the expansion of 

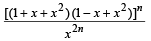
= Coeff. of x²ⁿ in the expansion of (1 + x² + x⁴)ⁿ But replacing x by x² in eq’s (1), we have

(1 + x² + x⁴)ⁿ = a₀ + a₁x² +....+ a_2n (x²)²ⁿ
∴Coeff of x²ⁿ = a_n 
Hence we obtain,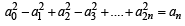

Q.20. Using mathematical induction prove that for every integer n ≥ 1, (3²ⁿ–1) is divisible by 2ⁿ⁺² but not by 2ⁿ⁺³. (1996 - 3 Marks)

 Ans. Sol.  For n = 1, 3^{2 n} - 1=3²¹ - 1 =9 - 1= 8 which is  divisible by 2ⁿ⁺² = 2³ = 8 but is not divisible by  2ⁿ⁺³ = 2⁴ = 16
Therefore, the result is true for n = 1.
Assume that the result is true for n = k.
That is, assume that 3^{2 k} –1 is divisible by 2 ^{k + 2} but is  not divisible by 2^{k + 3},
Since 3^{2 k} –1 is divisble by 2^{k + 2} but not by 2^{k + 3},
we can write 3^{2 k} –1= (m) 2^{k + 2} where m must be an odd positive integer, for otherwise 3^2k – 1 will become divisible by 2^{k + 3}.

For n = k +1, we have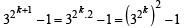

= (m.2^{k + 2} + 1)² – 1 [Using (1)]
= m².(2^{k + 2})² + 2m.2^{k + 2} + 1–1
= m².2^{2k + 4} + m.2^{k + 3} 
= 2^{k + 3}(m².^{2k + 1} + m.)
⇒ 3^2k+1– 1 is divisible by 2^{k +3} .
But 3^{2k +1} – 1 is not divisible by 2^{k + 4} for otherwise we must have 2 divides m². 2^k+1+ m.
But this is not possible as m is odd.
Thus, the result is true for  n = k + 1.

Q.21. Let 0 < A_i < p for i = 1, 2 ...., n. Use mathematical induction to prove that

sin A₁ + sin A₂ ... + sin A_n ≤ n sin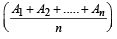 

where ≥ 1 is a natural number. {You may use the fact that p sin x + (1–p) sin y ≤ sin [px + (1–p)y],   where 0 ≤ p ≤ 1 and 0 ≤ x, y ≤ π} (1997 - 5 Marks)

Ans. 

Sol.  For n = 1, the inequalitity becomes sin A₁ ≤ sinA₁ , which is clearly true.
Assume that the inequality holds for n = k where k is some positive integer. That is, assume that

sin A₁ + sin A₂ + .... + sin A_k ≤ k sin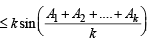 ....(1)
for same positive integer k.
We shall now show that the result holds for n = k + 1 that is, we show that

sin A₁ + sin A₂ + .... + sin A_k+ sinA_{k +1}

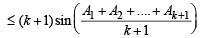....(2)

L.H.S. of (2) =  sin A₁ + sin A₂ + .... + sin A_k+ sinA_{k +1}

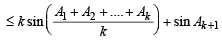
[Induction assumption]

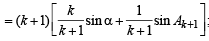
where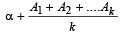  

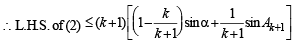
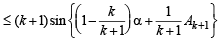
[Using the fact p sin x + (1– p) sin y ≤ sin [px + (1– p)y]

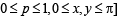
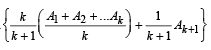
Thus, the inequality holds for n = k + 1. Hence, by the principle of mathematical induction the inequality holds for all n∈ N.

Q.22. Let p be a prime and m a positive integer. By mathematical induction on m, or otherwise, prove that whenever r is an integer such that p does not divide r, p divides ^mpC_r, (1998 - 8 Marks)
 [Hint: You may use the fact that (1+x)^(m+1)p = (1 + x)^p (1 + x)^mp]

Ans. Sol.  We know that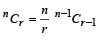 

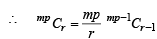
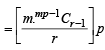
Now, L.H.S is an integer
⇒ RHS must be an integer
But p and r are coprime (given)

∴r must divide m. ^mp-1C_{r -1}

or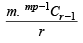is an integer..

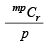⇒is an integer or ^mpC_r is divisible by p.

Q.23. Let n be any positive integer. Prove that (1999 - 10 Marks)

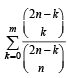
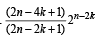
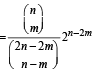
for each non-be gatuve integer m ≤ n.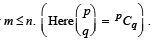

Ans. Sol.  

Let    P(m) =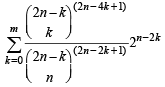 

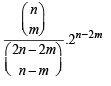=  ....(1)

For m = 0, LHS  =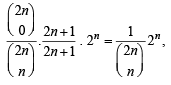 

R.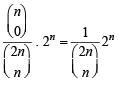H.S. = = LHS

[∵ m = 0 ⇒ k = 0]
∴P(0) holds true. Now assuming P (m)
L.H.S. of   P(m + 1) = L.H.S.  of

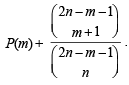
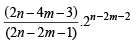
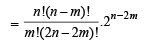
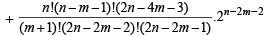
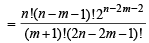
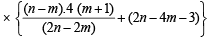
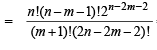
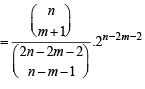
= R.H.S.  of   P(m + 1).
Hence by mathematical induction, result follows for all 0 ≤ m ≤ n.

Q.24. For any positive integer m, n (with n ≥ m), let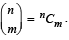  

Prove that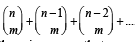 

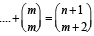
Hence or otherwise, prove that

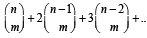
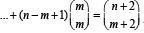    (2000 - 6 Marks)

Ans. Sol.  Given that for positive integers m and n such that n ≥m, then to prove that
ⁿC_m + ^{n – 1}C_m + ^{n – 2}C_m +....+ ^mC_m = ^{n + 1}C_{m + 1} 
L.H.S. ^mC_m + ^{m + 1}C_m + ^{m + 2}C_m +....+ ^n–1C_m + ⁿ C_m
[writing L.H.S. in reverse order]
= (^{m + 1}C_m+1 + ^{m + 1}C_m) + ^{m + 2}C_m +....+ ^n–1C_m + ⁿ C_m
[∵ ^mC_m = ^{m + 1}C_m+1]
= (^{m + 2}C_{m + 1} + ^{m + 2}C_m) + ^{m + 3}C_m +....+ ⁿC_m
[∵ ⁿC_{r + 1} + ⁿC_r= ⁿ⁺¹C_{r + 1}]
= ^{m + 3}C_{m + 1} + ^{m + 3}C_m +....+ ⁿC_m
Combining in the same way we get
= ⁿC_{m + 1} + ⁿC_m = ^{n + 1}C_{m + 1}= R.H.S.
Again we have to prove ⁿC_{m + 2} ^{n – 1}C_{m +3} ^{n – 2}C_m +....+ (n – m + 1) ^mC_m = ^{n + 2}C_{m + 2} 
= [ⁿC_m + ^{n – 1}C_{m +} ^{n – 2}C_m +....+ ^mC_m] + [ ^{n – 1}C_m  + ^{n – 2}C_m +....+ ^mC_m ] + [ ^{n – 2}C_m +....+ ^mC_m ] +....+ [ ^mC_m]
[n – m + 1 bracketed terms] = ^{n + 1}C_{m + 1} + ⁿC_{m + 1} ^{n – 1}C_m+1 ....+ ^{m + 1}C_{m + 1} 
[using previous result.]
= ^{n + 2}C_{m + 2}
[Replacing n by n + 1 and m by m + 1 in the previous result.] = R.H.S.

Q.25. For every positive integer n, prove that

Hence or other wise,

prove that 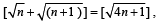 where [x] denotes the greatest integer not exceeding x. (2000 - 6 Marks)

Ans. Sol.  For n > 0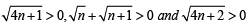 

Now,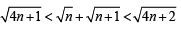to be proved.

I. To prove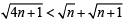

Squaring both sides in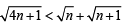 

⇒ 4n +1< n + n +1+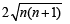

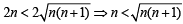⇒which is true.

II. To prove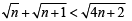 

Squaring both sides,

n + n + 1 +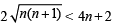

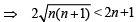 Squaring again

4 [n (n + 1)] < 4n² + 1+ 4n or 0 < 1 which is true

Hence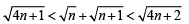

Further to prove 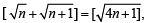 we  have to prove that there is no positive integer which lies between

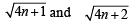or 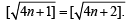 Using Mathematical induction.

We have to check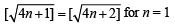  

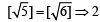 = 2, which is true 

Assume for n = k (arbitrary)

i.e., 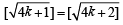 To prove for n = k +1

To check 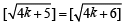  since k ≥ 0

Here 4k + 5 is an odd number and 4k + 6 is even number.
Their greatest integer will be different iff 4k + 6 is a perfect square that is 4k + 6 = r²

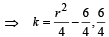is not integer. But k has to be integer..
So 4k + 6 cannot be perfect square.

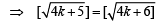
By Sandwich theorem

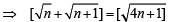
Q.26. Let a, b, c be positive real numbers such that b² - 4ac > 0 and let α₁ = c. Prove by induction that

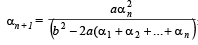 is well - defined and

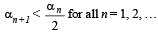  (Here, ‘well - defined’ means that the denominator in the expression for α_{n + 1} is not zero.) (2001 - 5 Marks)

Ans. Sol.  We have a, b, c the +ve real number s.t. b² – 4ac > 0; α₁= c.

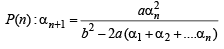
is well defined and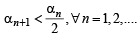  

For n = 1,  

Now, b² – 4ac > 0 ⇒ b² – 2ac > 2ac > 0

∴  α² is well defined (as denomination is not zero)

Also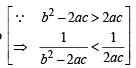 

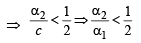
∴P(n) is true for n =1.
Let the statement be true for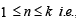  

 is well defined

and  

Now, we will prove that P(k + 1) is also true

i.e.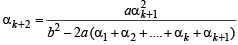 

well defined and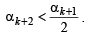  

We have

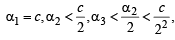
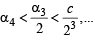  (by IH)

Now,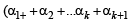  

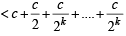
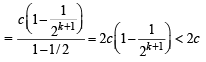
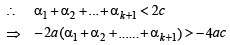
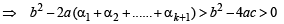
∴α_{k + 2} is well defined. Again by IH we have

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

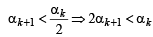
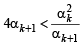
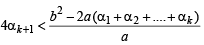
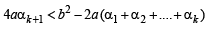
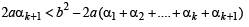
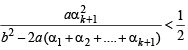
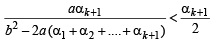
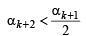
∴P(k+1) is also true.
Thus by the Principle of Mathematical Induction the Statement P(n) is true ∀ n∈ N .

Q.27. Use mathematical induction to show that (25)ⁿ⁺¹ – 24n + 5735 is divisible by (24)² for all n = 1, 2, ........ (2002 - 5 Marks)

Ans. Sol.  Let P(n) : (25) ^{n + 1} – 24n + 5735 For n = 1.
P(1)   : 625  – 24 + 5735 = 6336 = (24)2 ×  (11),
which is divisible by 242.
Hence P(1) is true Let P(k) be true, where k ≥ 1
⇒ (25) ^{k + 1} – 24k + 5735
= (24)²λ where λ ∈ N
For n = k + 1,
P (k + 1)  :  (25) k + 2 – 24 (k + 1) + 5735
= 25 [ (25) k + 1 – 24k + 5735]
+ 25.24.k – (25) (5735) + 5735 – 24 (k + 1)
= 25 (24) ² λ + (24)² k – 5735 × 24 – 24
= 25 (24)² λ + (24)² k – (24) (5736)
= 25 (24) ² λ+ (24) ² k – (24) ² (239),
= (24)² [25 λ + k – 239]
which is divisible by (24)2.
Hence, by the method of mathematical induction result is true ∀ n∈ N .

Q.28. Prove that             (2003 - 2 Marks)

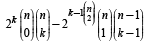
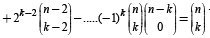
Ans. Sol.  To prove that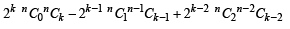

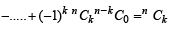
LHS of above equation can be written as

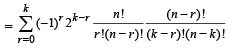
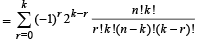
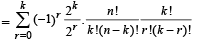
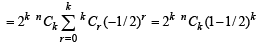
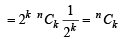R.H.S.  Hence Proved 

Q.29. A coin has probability p of showing head when tossed. It is tossed n times. Let p_n denote the probability that no two (or more) consecutive heads occur. Prove that p₁=1,  p₂=1–p² and p_n=(1– p).  p_n–1 + p(1 – p) p_n–2  for all n ≥ 3 .
 Prove by induction on n, that 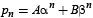 for all n ≥ 1 , where a and b are the roots of quadratic equation

 x²– (1 – p) x–p (1– p)=0 and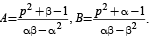 

Ans. Sol.  We have α + β = 1 – p and αβ = – p (1– p)
For n = 1, p_n = p₁ = 1

Also,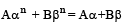 

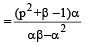
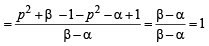
For n = 2, p₂ = 1– p²

Also, 

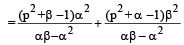
which is true for n = 2
Now let result is true for k < n where n ≥ 3.

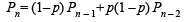
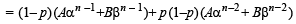
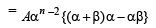
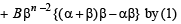
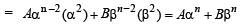
This is true for n. Hence by principle of mathematical induction, the result holds good for all n ∈ N .