Basics Concepts: Inverse Trigonometric Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
What is an Inverse Function?
- A function accepts values, performs particular operations on these values, and generates an output. The inverse function agrees with the resultant, operates, and reaches back to the original function.
- If y=f(x) and x=g(y) are two functions such that f (g(y)) = y and g (f(y)) = x, then f and y are said to be inverse of each other.
Example: If f(x) = 2x + 5 = y, then, g(y) = (y-5)/2 = x is the inverse of f(x). - The inverse of f is denoted by f -1
Inverse Trigonometric Functions
- Trigonometric functions are many-one functions but we know that inverse of function exists if the function is bijective.
- If we restrict the domain of trigonometric functions, then these functions become bijective and the inverse of trigonometric functions are defined within the restricted domain.
- Example: y = f(x) = sin x, then its inverse is x = sin-1 y.
Inverse Trigonometric Formulas
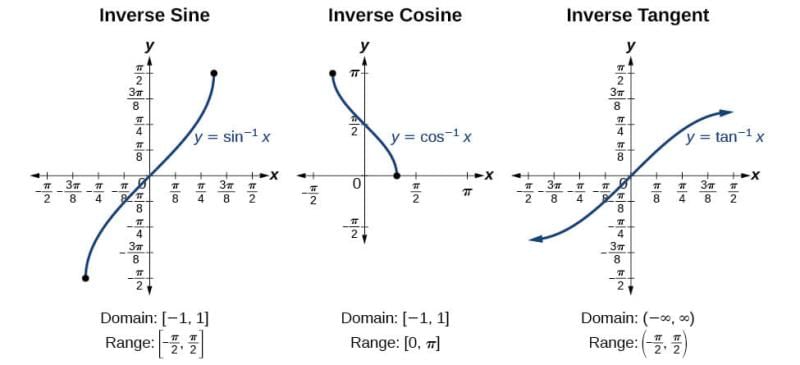 Fig: Inverse Trigonometric Functions
Fig: Inverse Trigonometric Functions
The inverse trigonometric functions are the inverse functions of the trigonometric functions written as cos-1 x, sin-1 x, tan-1 x, cot-1 x, cosec-1 x, sec-1 x.
The inverse trigonometric functions are multivalued. For example, there are multiple values of ω such that z = sinω, so sin-1z is not uniquely defined unless a principal value is defined.
Such principal values are sometimes denoted with a capital letter so, for example, the principal value of the inverse sine may be variously denoted sin-1z or arcsinz.
Let’s say, if y = sin x , then x = sin-1 y, similarly for other trigonometric functions. This is one of the inverse trigonometric formulas. Now, y = sin-1 (x), y ∈ [π/2 , π/2] and x ∈ [-1,1].
- Thus, sin-1 x has infinitely many values for given x ∈ [-1, 1].
- There is only one value among these values which lies in the interval [π/2, π/2]. This value is called the principal value.
Domain and Range of Inverse Trigonometric Formulas
| Function | Domain | Range |
| sin-1x | [-1,1] | [-π/2,π/2] |
| cos-1x | [-1,1] | [0,π] |
| tan-1x | R | (-π/2,π/2) |
| cot-1x | R | (0,π) |
| sec-1x | R-(-1,1) | [0,π]-{π/2} |
| cosec-1x | R-(-1,1) | [-π/2,π/2]-{0} |
Solved Examples
Ques 1: Find the exact value of each expression without a calculator, in [0,2π).
- sin-1(−3√2)
- cos-1(−2√2)
- tan-1√3
Ans:
- Recall that −3√2 is from the 30−60−90 triangle. The reference angle for sin and 3√2 would be 60∘. Because this is sine and it is negative, it must be in the third or fourth quadrant. The answer is either 4π/3 or 5π/3.
- −2√2is from an isosceles right triangle. The reference angle is then 45∘. Because this is cosine and negative, the angle must be in either the second or third quadrant. The answer is either 3π/4 or 5π/4.
- √3is also from a 30−60−90 triangle. Tangent is √3 for the reference angle 60∘. Tangent is positive in the first and third quadrants, so the answer would be π/3 or 4π/3.
Notice how each one of these examples yields two answers. This poses a problem when finding a singular inverse for each of the trig functions. Therefore, we need to restrict the domain in which the inverses can be found.
Ques 2: Find the value of tan-1(1.1106).
Ans: Let A=tan−1(1.1106)
Then, tanA = 1.1106
A = 48°
tan48 = 1.1106
[Use calculator in degree mode]
tan−1 1.1106=48°
Properties of Inverse
Here are the properties of the inverse trigonometric functions with proof.
Property 1
- sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1
- cos-1 (1/x) = sec-1x , x ≥ 1 or x ≤ -1
- tan-1 (1/x) = cot-1x , x > 0
Proof : sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1,
Let sin−1x=y
i.e. x = cosec y
1/π = sin y
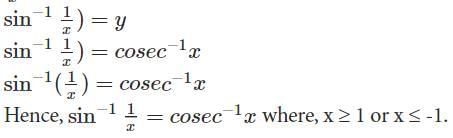
Property 2
- sin-1(-x) = – sin-1(x), x ∈ [-1,1]
- tan-1(-x) = -tan-1(x), x ∈ R
- cosec-1(-x) = -cosec-1(x), |x| ≥ 1
Proof: sin-1(-x) = -sin-1(x), x ∈ [-1,1]
Let, Sin-1(-x) = y
Then −x=sin y
x=−sin y
x=sin(−y)
sin−1=sin−1(sin(−y))
sin−1x=y
sin−1x=−sin−1(−x)
Hence,sin−1(−x)=−sin−1 x ∈ [-1,1]
Property 3
- cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
- sec-1(-x) = π – sec-1x, |x| ≥ 1
- cot-1(-x) = π – cot-1x, x ∈ R
Proof : cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
Let cos−1(−x)=y
cos y=−x x=−cos y
x=cos(π−y)
Since, cos π−q=−cos q
cos−1 x=π−y
cos−1 x=π–cos−1–x
Hence, cos−1−x=π–cos−1x
Solved Example
Ques 1: Prove that “sin-1(-x) = – sin-1(x), x ∈ [-1,1]”
Ans: Let, sin−1(−x)=y
Then −x=sin y
x=−sin y
x=sin(−y)
sin−1 x=arcsin(sin(−y))
sin−1 x=y
sin−1 x=−sin−1(−x)
Hence, sin−1(−x)=−sin−1 x, x ∈ [-1,1]
This concludes our discussion on the topic of trigonometric inverse functions.
Ques 2: sin-1(cos π/3)=?
Ans: sin−1 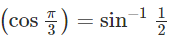 [substitute cos(π/3)=1/2]
[substitute cos(π/3)=1/2]
= π/6 [substitute sin-1 (1/2) = π/6]
Ques 3: Find the value of sin (π/4+Cos-1(√2/2)).
Ans:
Let y=sin 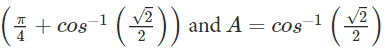
Then, cosA= √2/2
Multiplying the numerator as well as denominator by √2 we get:
cosA=1/√2
A = π/4
Therefore
y = sin 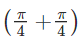
y = sin (π/2)
hence, y=1.
|
172 videos|476 docs|154 tests
|
FAQs on Basics Concepts: Inverse Trigonometric Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of an inverse function? |  |
| 2. How do inverse trigonometric functions relate to trigonometric functions? |  |
| 3. What are some examples of inverse trigonometric functions? |  |
| 4. How can inverse trigonometric functions be useful in real-life applications? |  |
| 5. Are there any restrictions on the domains of inverse trigonometric functions? |  |
















