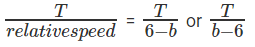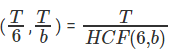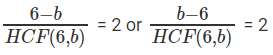Time, Speed and Distance: Solved Examples- 1 | General Aptitude for GATE - Mechanical Engineering PDF Download

Que 1: Two friends A and B simultaneously start running around a circular track. They run in the same direction. A travels at 6 m/s and B runs at b m/s. If they cross each other at exactly two points on the circular track and b is a natural number less than 30, how many values can b take?
(A) 3
(B) 4
(C) 7
(D) 5
Ans: Option (A)
Explanation:Let track length be equal to T.
Time taken to meet for the first time =
Time taken for a lap for A = T/6
Time taken for a lap for B = T/b
So, time taken to meet for the first time at the starting point = LCM
Number of meeting points on the track = Time taken to meet at starting point/Time taken for first meeting = Relative speed / HCF (6,b).
So, in essence we have to find values for b such that
b = 2, 10, 18 satisfy this equation. So, there are three different values that b can take.
Hence, the answer is 3.
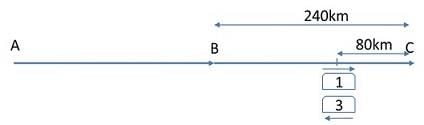
Que 2: Three cars leave A for B in equal time intervals. They reach B simultaneously and then leave for Point C which is 240 km away from B. The first car arrives at C an hour after the second car. The third car, having reached C, immediately turns back and heads towards B. The first and the third car meet a point that is 80 km away from C. What is the difference between the speed of the first and the third car?
(A) 60 kmph
(B) 20 kmph
(C) 40 kmph
(D) 80 kmph
Ans: Option (A)
Explanation:
Que 3: Suraj drives the first 120 km in 2 hrs and the next 180 km in the next 4 hrs. What is his average speed for the entire trip in km per hour?
(A) 50 kmph
(B) 40 kmph
(C) 70 kmph
(D) 80 kmph
Ans: Option (A)
Explanation: Total Distance travelled = 120 + 180 = 300 km.
Total Time taken = 2 + 4 = 6 hrs.Average Speed =Total Distance Travelled/Total Time Taken = 300/6 = 50 km/hr.
Que 4: Running at a speed of 60 km per hour, a train passed through a 1.5 km long tunnel in two minutes. What is the length of the train?
(A) 250 m
(B) 500 m
(C) 1000 m
(D) 1500 m
Ans: Option (B)
Explanation: Step 1: Convert the speed into meters per second
The given speed is 60 km/h.
To convert it into meters per second (m/s), we multiply by 5/18Speed = (60 × 5/18) = 16.67 m/s
Step 2: Convert the time into seconds
The time given is 2 minutes. To convert it into seconds:Time = 2 × 60 = 120 seconds
Step 3: Calculate the total distance covered
The total distance covered by the train in 2 minutes is:Distance = 16.67 m/s × 120 seconds = 2000 meters
Step 4: Subtract the length of the tunnel
The total distance covered includes the length of the train and the tunnel.
The length of the tunnel is 1.5 km, or 1500 meters.
Therefore, the length of the train is: 2000 meters - 1500 meters = 500 metersThus, the length of the train is 500 meters.
Que 5: A runner can complete a 750 m race in two and a half minutes. Will he be able to beat another runner who runs at 17.95 km/hr?
(A) Yes
(B) No
Ans: Option (A).
Explanation: We are given that the first runner can complete a 750 m race in 2 minutes and 30 seconds or 150 seconds.=> Speed of the first runner = 750 / 150 = 5 m / sec
We convert this speed to km/hr by multiplying it by 18/5.
=> Speed of the first runner = 18 km / hr
Also, we are given that the speed of the second runner is 17.95 km/hr.
Therefore, the first runner can beat the second runner.
Hence, the answer is Yes.
Que 6: A man decided to cover a distance of 6 km in 84 minutes. He decided to cover two-thirds of the distance at 4 km/hr and the remaining at some different speed. Find the speed after the two-thirds distance has been covered.
(A) 5.5 kmph
(B) 4 kmph
(C) 5 kmph
(D) 3 kmph
Ans: Option (C)
Explanation: We are given that two-thirds of the 6 km was covered at 4 km/hr.=> 4 km distance was covered at 4 km/hr.
=> Time taken to cover 4 km = 4 km / 4 km / hr = 1 hr = 60 minutes
=> Time left = 84 – 60 = 24 minutes
Now, the man has to cover the remaining 2 km in 24 minutes or 24 / 60 = 0.4 hours
=> Speed required for remaining 2 km = 2 km / 0.4 hr = 5 km / hr
Que 7: A postman traveled from his post office to a village in order to distribute mail. He started on his bicycle from the post office at a speed of 25 km/hr. But, when he was about to return, a thief stole his bicycle. As a result, he had to walk back to the post office on foot at the speed of 4 km/hr. If the traveling part of his day lasted for 2 hours and 54 minutes, find the distance between the post office and the village.
(A) 20 km
(B) 10 km
(C) 30 km
(D) 40 km
Ans: Option (B).
Explanation: Let the time taken by postman to travel from post office to village= t minutes.
According to the given situation,
Distance from post office to village, say d1=(25/60) x t kmDistance from village to post office, say d2=4/60 x (174-t) km as 2 hours 54 minutes = 174 minutes
Since distance between village and post office will always remain same i.e. d1 = d2
=> 25/60 x t = 4/60 x (174-t)
Upon solving , we get
=> t = 24 minutes.=> Distance between post office and village = speed x time
=>25/60 x 24 = 10km
Que 8: Two friends A and B leave City P and City Q simultaneously and travel towards Q and P at constant speeds. They meet at a point in between the two cities and then proceed to their respective destinations in 54 minutes and 24 minutes, respectively. How long did B take to cover the entire journey between City Q and City P?
(A) 60
(B) 36
(C) 24
(D) 48
Ans: Option (A)
Explanation: Let us assume Car A travels at a speed of a and Car B travels at a speed of b.
Further, let us assume that they meet after t minutes.Distance traveled by car A before meeting car B = a x t.
Likewise distance traveled by car B before meeting car A = b x t.Distance traveled by car A after meeting car B = a x 54
Distance traveled by car B after meeting car A = 24 x b.Distance traveled by car A after crossing car B = distance traveled by car B before crossing car A (and vice versa).
=> at = 54b --------- (1)
and bt = 24a ------- (2)Multiplying equations 1 and 2
we have ab x t2 = 54 x 24 x ab
=> t2 = 54 x 24
=> t = 36
Or, B would have taken 36 + 24 = 60 minutes to travel the whole distance.Hence, the answer is 60 mins.
Que 9: Two trains of equal lengths take 13 seconds and 26 seconds, respectively, to cross a pole. If these trains are moving in the same direction, then how long will it take to cross each other?
(A) 40 seconds
(B) 50 seconds
(C) 39 seconds
(D) 52 seconds
Ans: Option (D)
Explanation: Train A takes 13 seconds to cross a pole.
Train B takes 26 seconds to cross a pole.
Let the length of each train be L.
→ Speed of train A = L/13,
Speed of train B = L/26.
When the two trains cross each other, the total distance covered is 2L (length of train A + length of train B).
Relative speed of the two trains = speed of train A - speed of train B = L/13 - L/26 = L/26.
Time taken to cross each other = total distance / relative speed = 2L / (L/26) = 52 seconds.
Hence, the two trains take 52 seconds to cross each other.
Que 10: A policeman noticed a thief from 300 m. The thief started running and the policeman was chasing him. The thief and the policeman ran at speeds of 8 km/h and 9 km/h, respectively. What was the distance between them after 3 minutes?
(A) 225 m
(B) 250 m
(C) 300 m
(D) 200 m
Ans: Option (B)
Explanation: Distance between policeman and thief in the starting = 300 m
Speed of policeman = 9 km/hr Speed of thief = 8 km/hr
If the speed of a policeman and thief is x km/hr and y km/hr, then Relative speed, if same directions = (x - y) km/hr Distance between them after n hrs = (x - y) × n 1 km/hr = 5/18 m/sec 1 min = 60 sec
3 min = 3 × 60 = 180 seconds
Distance between policeman and thief in starting = 300 m
Relative speed of policeman and thief, if same directions = (9 - 8) = 1 × (5/18) = (5/18) m/sec
Distance covered in 180 seconds = (5/18) × 180 = 50 m
Distance between them after 180 seconds= 300 - 50 = 250 m
∴ Distance between them after 3 min is 250 m.
|
206 videos|190 docs|158 tests
|
FAQs on Time, Speed and Distance: Solved Examples- 1 - General Aptitude for GATE - Mechanical Engineering
| 1. What are the basic concepts of speed, time, and distance? |  |
| 2. How is speed calculated using time and distance? |  |
| 3. How can I calculate the time taken to cover a certain distance at a given speed? |  |
| 4. What happens to the time taken when the speed increases? |  |
| 5. Can you provide an example of calculating distance when speed and time are known? |  |