Class 10 Maths Chapter 8 Previous Year Questions - Introduction to Trigonometry
Previous Year Questions 2025
Q1: If tan A+ cot A= 6, then find the value of tan2A + cot2 A - 4.
 View Answer
View Answer 
Ans: We have, tanA + cotA = 6
On squaring both sides, we get (tanA + cotA)2 = 36
⇒ tan2A + cot2A + 2 tanA cotA = 36
Since tan A cot A = 1
⇒ tan2A + cot2A + 2 = 36
⇒ tan 2A + cot 2A = 36 - 2 = 34 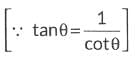
∴ tan2A + cot2A - 4 = 34 - 4 = 30
Q2: If tan 3θ = √3, then θ/2 equals
(a) 60°
(b) 30°
(c) 20°
(d) 10°
 View Answer
View Answer 
Ans: (d)
We have, tan3θ = √3
⇒ tan3θ = tan 60° 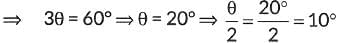
Q3: If sin 4θ = √3/2, then θ/3 equals:
(a) 60°
(b) 20°
(c) 15°
(d) 5°
 View Answer
View Answer 
Ans: (d)
Given, sin 4θ = √3/2 = sin 60°.
⇒ 4θ = 60°
⇒ θ = 15°.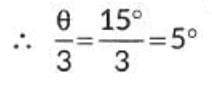
Q4: If α + β = 90° and α = 2β, then cos2α + sin2β is equal to:
(a) 0
(b) 1/2
(c) 1
(d) 2
 View Answer
View Answer 
Ans: (b)
α + β = 90° and α = 2β ...(i)
∴ 2β + β = 90° ⇒ 3β = 90° ⇒ β = 30°
∴ α = 2 × 30° = 60° [From (i)]
∴ cos²α + sin²β = cos²60° + sin²30°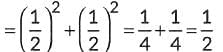
Q5:  then x : y =
then x : y =
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 4: 1
 View Answer
View Answer 
Ans: (c) 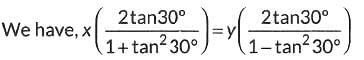
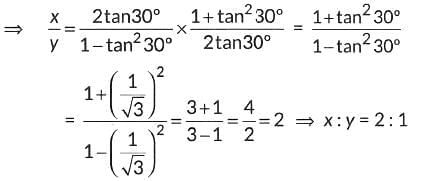
Q6: If 4k = tan260° - 2cosec2 30° - 2tan2 30°, then find the value of k.
 View Answer
View Answer 
Ans: Given, 4k = tan260° - 2 cosec230° - 2 tan230° 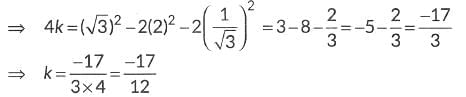
Q7: If x cos60° + ycos0° + sin30° - cot45° = 5, then find the value of x + 2y.
 View Answer
View Answer 
Ans: We have, x cos60° + y cos0° + sin30° - cot45° = 5 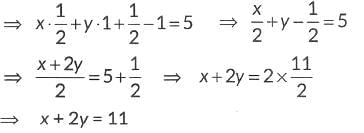
Q8: 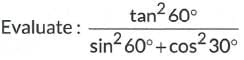
 View Answer
View Answer 
Ans: 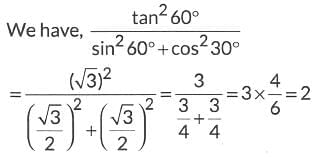
Q9: 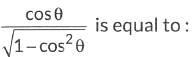
(a) cot θ
(b) 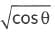
(c) 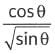
(d) tan θ
 View Answer
View Answer 
Ans: (a)
We have, 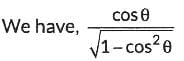
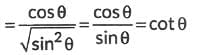 [∵ 1 - cos2θ = sin2θ]
[∵ 1 - cos2θ = sin2θ]
Q10: The value of (tan A cosec A)2 - (sin A sec A)2 is:
(a) 0
(b) 1
(c) -1
(d) 2
 View Answer
View Answer 
Ans: (b)
We have,
(tan A · cosec A)2 - (sin A . sec A)2
Using identities:
tan A = sin A / cos A,
cosec A = 1 / sin A,
sec A = 1 / cos A.
sec² A - tan² A = 1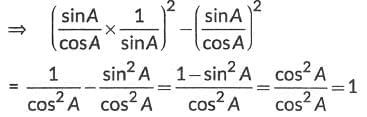
Q11: (cotθ + tanθ) equals:
(a) cosecθ secθ
(b) sinθ secθ
(c) cosθ tanθ
(d) sinθ cosθ
 View Answer
View Answer 
Ans: (a)
We have, cotθ + tanθ
cot θ = cos θ / sin θ,
tan θ = sin θ / cos θ.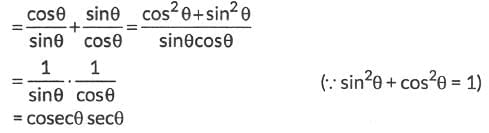
Q12: The value of 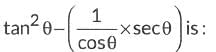
(a) 1
(b) 0
(c) -1
(d) 2
 View Answer
View Answer 
Ans: (c)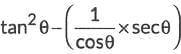

Q13: In a right triangle ABC, right-angled at A, if sin B = 1/4 then the value of sec B is
(a) 4
(b) √15/4
(c) √15
(d) 4/√15
 View Answer
View Answer 
Ans: (d)
Given, sin B = 1/4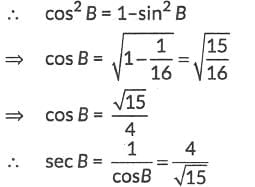
Q14: If a secθ + b tan θ = m and b sec θ + a tan θ = n, prove that a2 + n2 = b2 + m2
 View Answer
View Answer 
Ans:
We have, a sec θ + b tan θ = m
and b sec θ + a tan θ = n
Taking, m² - n²
= (a sec θ + b tan θ)² - (b sec θ + a tan θ)²
= a²sec²θ + b²tan²θ + 2ab tan θ sec θ - b²sec²θ - a²tan²θ - 2ab tan θ sec θ
= a²(sec²θ - tan²θ) + b²(tan²θ - sec²θ)
= a² × 1 + b² × (-1)
= a² - b²
∴ m² - n² = a² - b²
⇒ a² + n² = b² + m²
Hence, proved.
Q15: Use the identity: sin2A + cos2A = 1 to prove that tan2A + 1 = sec2A. Hence, find the value of tan A, where sec A = 5/3, where A is an acute angle.
 View Answer
View Answer 
Ans:
To prove: tan2A + 1 = sec2A
Taking L.H.S., tan2 A+ 1 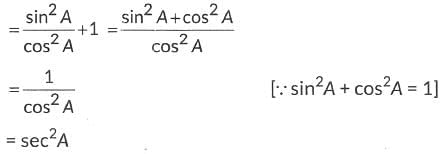
∴ L.H.S = R.H.S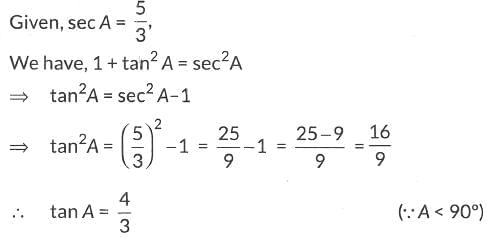
Q16: Prove that: 
 View Answer
View Answer 
Ans: 
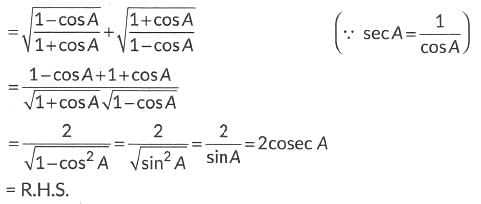
Q17: Prove that: 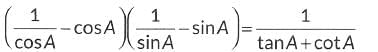
 View Answer
View Answer 
Ans: 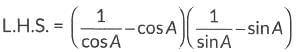
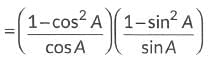
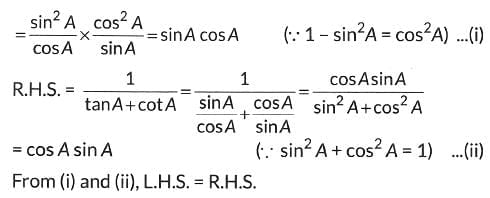
Q18: Prove that: 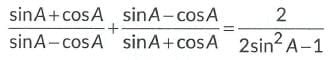
 View Answer
View Answer 
Ans: 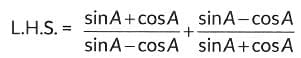
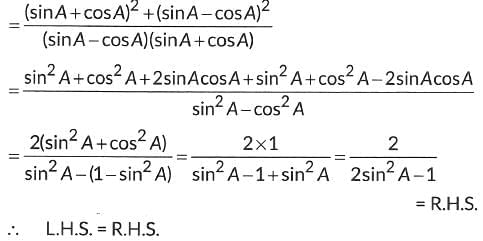
Q19: 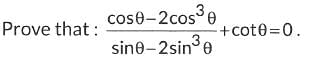
 View Answer
View Answer 
Ans: 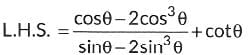
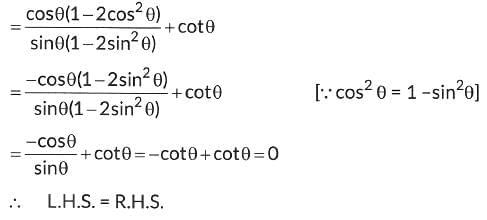
Q20: Given that sin 8 + cos 8 = x, prove that 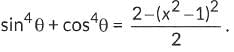
 View Answer
View Answer 
Ans: sin θ + cos θ = x ...(i)
Squaring both sides in equation (i),
sin² θ + cos² θ + 2sin θ cos θ = x²
2sin θ cos θ = x² - 1 ...(ii)
[∵ sin² θ + cos² θ = 1]
Also, sin² θ + cos² θ = (sin θ + cos θ)² - 2sin θ cos θ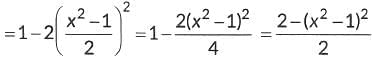
Q21: Prove that: 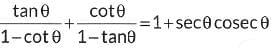
 View Answer
View Answer 
Ans: 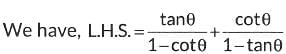
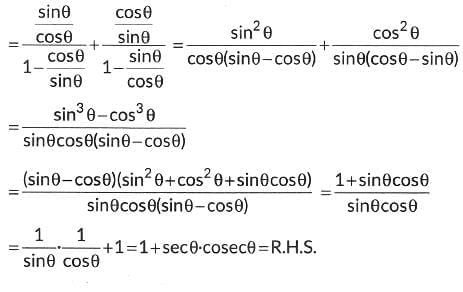
Previous Year Questions 2024
Q1: If sin α = √3/2, cos β = √3/2 then tan α. tan β is: (1 Mark) (CBSE 2024)(a) √3
(b) 1/√3
(c) 1
(d) 0
 View Answer
View Answer 
Ans: (c)
sin α = √3/2, ⇒ sin α = sin 60º
⇒ α = 60º
∵ cos β = √3/2,
⇒ cos β = cos 30º
⇒ β = 30º
tan α. tan β = tan 60º. tan 30º
= √3 x 1√3
= 1
Q2: Evaluate: 5 tan 60°(sin² 60° + cos² 60°) tan 30° (3 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
5 tan 60°(sin² 60° + cos² 60°) tan 30° = 5 × √31 × 1√3
= 5 × √3 × √3
= 5 × 3
= 15
Q3: Prove that: (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) = 1 (3 Marks) (CBSE 2024)
 View Answer
View Answer 
Ans:
L.H.S. = (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ)
= (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ)
Since, cosec θ = 1/sin θ, sec θ = 1/cos θ, tan θ = sin θ/cos θ, cot θ = cos θ/sin θ
= (1/sin θ – sin θ) (1/cos θ – cos θ) (sin θ/cos θ + cos θ/sin θ)
= 1 - sin2θsin θ × 1 - cos2θcos θ × sin2θ + cos2θsin θ . cos θ
= cos2θ × sin2θsin θ × cos θ × 1sin θ . cos θ
= sin θ . cos θ1 × 1sin θ . cos θ [ : sin2θ + cos2θ = 1 ]
= 1 = R.H.S.
Hence, proved.
Previous Year Questions 2023
Q1: If 2 tan A = 3, then find the value of 4 sin A + 5 cos A6 sin A + 2 cos A is (3 Marks)(2023) View Answer
View Answer 
Ans: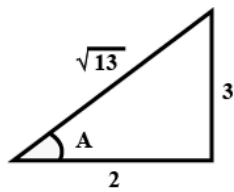
Given:
2 tan A = 3 ⇒ tan A = 3/2
Using sin2 A + cos2 A = 1, let:
sin A = 3/√13, cos A = 2/√13
Substituting in the given expression:
4 sin A + 5 cos A6 sin A + 2 cos A
= 4 × 3/√13 + 5 × 2/√136 × 3/√13 + 2 × 2/√13
= 12/√13 + 10/√1318/√13 + 4/√13
= 22/√1322/√13
= 1
Q2: 5/8 sec260° - tan260° + cos245° is equal to (1 Mark) (2023)
(a) 5/3
(b) -1/2
(c) 0
(d) -1/4
 View Answer
View Answer 
Ans: (c)
Sol:
58 × (2)2 - (√3)2 + (1√2)2 = 5/8 × 4 - 3 + 12 = 0
Q3: Evaluate 2 sec2θ + 3 cosec2θ - 2 sin θ cos θ if θ = 45° (2 Marks) (CBSE 2023)
 View Answer
View Answer 
Ans: Since θ = 45°, sec 45° = √2, cosec 45° = √2, sin 45° = 1/√2 cos 45° = 1/√2
2sec2 θ + 3 cosec2 θ – 2 sin θ cos θ
= 2 (√2)2 + 3 (√2)2 - 2 (1√2) × (1√2)
= 2 × 2 + 3 × 2 - 2 × 12
= 4 + 6 - 1
= 9
Q4: Which of the following is true for all values of θ(0o ≤ θ ≤ 90o)? (1 Mark) (2023)
(a) cos2θ - sin2θ - 1
(b) cosec2θ - sec2θ- 1
(c) sec2θ - tan2θ - 1
(d) cot2θ- tan2θ = 1
 View Answer
View Answer 
Ans: (c)
Option (a): cos²θ - sin²θ - 1
Using the identity: cos²θ - sin²θ = cos 2θ, we get cos²θ - sin²θ - 1 = cos 2θ - 1, which is not always true. So, this option is incorrect.
Option (b): cosec²θ - sec²θ - 1
Using the identities cosec²θ = 1 + cot²θ and sec²θ = 1 + tan²θ,
we get cosec²θ - sec²θ - 1 = (1 + cot²θ) - (1 + tan²θ) - 1 = cot²θ - tan²θ - 1, which is not always zero. So, this option is incorrect.
Option (c): sec²θ - tan²θ - 1
Using the identity sec²θ = 1 + tan²θ,
we get sec²θ - tan²θ - 1 = (1 + tan²θ) - tan²θ - 1 = 0, which is always true.
So, this option is correct.
Option (d): cot²θ - tan²θ = 1
Using the identity cot²θ = 1/tan²θ, we get cot²θ - tan²θ = (1/tan²θ) - tan²θ, which is not always equal to 1. So, this option is incorrect.
Q5: If sinθ +cosθ = √3. then find the value of sinθ. cosθ. (3 Marks) (2023)
 View Answer
View Answer 
Ans: Given, sinθ +cosθ = √3
Squaring both sides, we get (sinθ + cosθ)2 = (√3)2
⇒ sin2θ + cos2θ + 2sinθ cosθ = 3 ( ∵ sin2θ + cos2θ = 1)
⇒ 1 + 2sinθ cosθ = 3
⇒ 2sinθ cosθ = 3 - 1
⇒ 2sinθ cosθ = 2
⇒ sinθ cosθ = 1
Q6: If sin α = 1/√2 and cot β = √3, then find the value of cosec α + cosec β. (3 Marks) (2023)
 View Answer
View Answer 
Ans: Given, sin α = 1/√2 and cot β = √3
We know that, cosec α = 1/sinα = √2
Also, 1 + cot2β = cosec2β
⇒ cosec2β = 4
⇒ cosec β = √4 = 2
Now, cosec α + cosec β = √2 + 2
Q7: Prove that the Following Identities: Sec A (1 + Sin A) ( Sec A - tan A) = 1 (3 Marks) (2023)
 View Answer
View Answer 
Ans: LHS = sec A(1 + sin A )( sec A - tan A)
= 1cos A (1 + sin A) 1cos A - sin Acos A
= 1cos A (1 + sin A) (1 - sin Acos A)
= 1 - sin² Acos² A = cos² Acos² A
= 1
= RHS
Hence proved..
Q8: (sec2 θ – 1) (cosec2 θ – 1) is equal to: (1 Mark) (CBSE 2023)
(a) –1
(b) 1
(c) 0
(d) 2
 View Answer
View Answer 
Ans: (b)
(sec²θ - 1) (cosec²θ - 1) = tan²θ . cot²θ
tan²θtan²θ [ ∵ sec²θ - 1 = tan²θ & cosec²θ - 1 = cot²θ ]
= 1
Q9: If sin θ – cos θ = 0, then find the value of sin4 θ + cos4 θ. (2 Marks) (CBSE 2023)
 View Answer
View Answer 
Ans: Given,
sin θ – cos θ = 0
sin θ = cos θ
tan θ = 1
tan θ = tan 45°
⇒ θ = 45°
Now, sin4 θ + cos4 θ = sin4 45° + cos4 45°
= (1√2)4 + (1√2)4
= 14 + 14 = 12
Q10: Prove that sin A - 2 sin3 A2 cos3 A - cos A = tan A (4 & 5 Marks) (CBSE 2023)
 View Answer
View Answer 
Ans:
LHS = sin A - 2 sin3 A2 cos3 A - cos A
= sin A (1 - 2 sin² A)cos A (2 cos² A - 1)
= sin A (1 - 2 (1 - cos² A)cos A (2 cos² A - 1)
= tan A 1 - 2 + 2 cos² A2 cos² A - 1
= tan A 2 cos² A - 12 cos² A - 1
= tan A
= RHS
Previous Year Questions 2022
Q1: Given that cos θ = √3/2, then the value of cosec2θ - sec2θcosec2θ + sec2θ3 is (2022)(a) -1
(b) 1
(c) 1/2
(d) -1/2
 View Answer
View Answer 
Ans: (c)
Sol:
Given, cosθ = √3/2 = B/H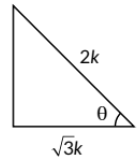
Let B = √3k and H = 2k
∴ P = √((2k)2 - (√3k)2) [By Pythagoras Theorem]
⇒ k2 = k
∴ cosec θ = H / p = 2k / k = 2
sec θ = H / B = 2k / √3k = 2 / √3
cosec2θ - sec2θ = (2)2 - (2 / √3)24 - 4/3
= 4 - 43 = 83
cosec2θ + sec2θ = (2)2 + (2 / √3)24 + 4/3
= 4 + 43 = 163
Q2: 1cosec θ (1 - cot θ) + 1sec θ (1 - tan θ) is equal to (2022)
(a) 0
(b) 1
(c) sinθ + cosθ
(d) sinθ - cosθ
 View Answer
View Answer 
Ans: (c)
Sol: We have,
1cosec θ (1 - cot θ) + 1sec θ (1 - tan θ)
= sin θcos θ / 1 - cos θsin θ + 1 - sin θ1 - cos θ
= 1cosec θ = sin θcos θ, 1sec θ
= sin2 θcos2 θ = sin2 θ - cos2 θsin θ - cos θ
= sin θ + cos θ
Q3: The value of θ for which 2 sin2θ = 1, is (2022)
(a) 15°
(b) 30°
(c) 45°
(d) 60°
 View Answer
View Answer 
Ans: (a)
Sol: Given, 2 sin2θ = 1 ⇒ sin2θ = 1/2
⇒ 2θ = 30°
⇒ θ = 15°
Q4: If sin2θ + sinθ = 1, then find the value of cos2θ + cos4θ is (2022)
(a) -1
(b) 1
(c) 0
(d) 2
 View Answer
View Answer 
Ans: (b)
Sol: Given, sin2θ + sinθ = 1 ---(i)
sinθ = 1 - sin2θ
⇒ sinθ = cos2θ ---(ii)
∴ cos2θ + cos4θ
= sinθ + sin2θ [From (ii)]
= 1 [From (i)]
Previous Year Questions 2021
Q1: If 3 sin A = 1. then find the value of sec A. (2021 C) View Answer
View Answer 
Ans: We have, 3 sin A = 1
∴ sin A = 1/3
Now by using cos2 A = 1 - sin2 A, we get
cos2 A = 1 - 19 = 89
⇒ cos A = 2√23
∴ sec A = 1cos A = 12√2 / 3 = 3√24
Q2: Show that: 1 + cot2θ1 + tan2θ = cot2θ (2021 C)
 View Answer
View Answer 
Ans: We have, L.H.S.
1 + cot2θ1 + tan2θ = cosec2θsec2θ
[By using 1 + tan2θ = sec2θ and 1 + cot2 θ = cosec2θ ]
⇒ 1sin2θ = cos2θsin2θ = cot2θ
Hence,
1 + cot2θ1 + tan2θ = cot2θ
Previous Year Questions 2020
Q1: If sin θ = cos θ, then the value of tan2 θ + cot2 θ is (2020)(a) 2
(b) 4
(c) 1
(d) 10/3
 View Answer
View Answer 
Ans: (a)
Sol: We have, sin θ = cos θ
or sin θ / cos θ = 1
⇒ tan θ = 1 and cot θ = 1 [∵ cot θ = 1/tanθ]
∴ tan2 θ + cot2 θ = 12 + 12 = 2
Hence, A option is correct.
Q2: Given 15 cot A = 8, then find the values of sin A and sec A. (2020)
 View Answer
View Answer 
Ans: In right angle ΔABC we have
15 cot A = 8
⇒ cot A = 8/15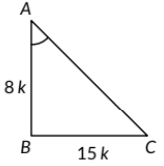
Since, cot A = AB/BC
∴ AB/BC = 8/15
Let AB = 8k and BC = 15k
By using Pythagoras theorem, we get
AC2 = AB2 + BC2
⇒ (8k)2 + (15)2 = 64k2 + 225k2 = 289k2 = (17k)2
⇒ AC = √((17k)2) = 17k
∴ sin A = BCAC = 15k17k = 1517
and cos A = ABAC = 8k17k = 817
So, sec A = 1cos A = 178
Q3: Write the value of sin2 30° + cos2 60°. (2020)
 View Answer
View Answer 
Ans: We have, sin2 30° + cos2 60°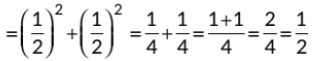
Q4: The distance between the points (a cos θ + b sin θ, 0) and (0, a sin θ − b cos θ) is (2020)
(a) a2 + b2
(b) a + b
(c) 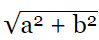
(d) 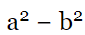
 View Answer
View Answer 
Ans: (c)
Sol: Given the point A (cos θ + b sin θ , 0), (0 , a sin θ − b cos θ)
By distance formula,
The distance of
AB = √(x2 - x1)² + (y2 - y1)²
So,
AB = √(a cos θ + b sin θ - 0)² + (0 - a sin θ + b cos θ)²
= √ a²(sin²θ + cos²θ) + b²(sin²θ + cos²θ)
But according to the trigonometric identity,
sin²θ + cos²θ = 1
Therefore,
AB = √ a² + b²
Q5: 5 tan2θ - 5 sec2θ = ____________. (2020)
 View Answer
View Answer 
Ans: We have 5(tan2θ - sec2θ)
= 5(-1) = - 5 [By using 1 + tan2θ = sec2 θ ⇒ tan2θ - sec2θ = - 1]
Q6: If sinθ + cosθ = √3. then prove that tan θ + cot θ = 1 (2020)
 View Answer
View Answer 
Ans: sin θ + cos θ =√3
= (sinθ + cosθ)2 = (√3)2
= sin2 θ + cos2 θ + 2sin θ cos θ = 3 (Since,sin2θ + cos2θ = 1)
= 1 + 2sin θ cos θ = 3
⇒ 2sin θ cos θ = 2
⇒ sin θ cos θ = 1
⇒ sin θ cos θ = sin2θ + cos2θ
⇒ 1 = sin2θ + cos2θsin θ cos θ
⇒ tan θ + cot θ = 1
Q7: If x = a sinθ and y = b cosθ, write the value of (b2x2 + a2y2). (CBSE 2020)
 View Answer
View Answer 
Ans: Given, x = a sin θ and y = b cos θ
Putting the values of x and y in (b2x2 + a2y2)
We get,
= b2(a sin θ)2 + a2(b cos θ)2
= a2b2 [sin2 θ + cos2 θ] [Also, sin2θ + cos2θ = 1]
= a2b2 [1]
= a2b2
Q8: Prove that: 2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = 0. (CBSE 2020)
 View Answer
View Answer 
Ans: We know that,
sin2 θ + cos2 θ = 1
So, (sin2 θ + cos2 θ) 2 = 12
⇒ sin4 θ + cos4 θ + 2sin2 θ cos2 θ = 1
i.e., sin4 θ + cos4 θ = 1 – 2 sin2 θ cos2 θ …(i)
Also, (sin2 θ + cos2 θ) 3 = 13
⇒ sin6 θ + cos6 θ + 3 sin2 θ cos2 θ (sin2 θ + cos2 θ) = 1
⇒ sin6 θ+ cos6 θ+ 3sin2 θ cos2 θ (1) = 1
i.e., sin6 θ + cos6 θ = 1 – 3 sin2 θ cos2 θ …(ii)
Now,
LHS = 2(sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ) + 1
= 2(1 – 3 sin2 θ cos2 θ) – 3(1 – 2 sin2 θ cos2 θ) + 1
= 2 – 3 + 1
= 0
Hence, proved.
Q9: Prove that: (sin4 θ – cos4 θ + 1) cosec2 θ = 2. [CBSE 2020].
 View Answer
View Answer 
Ans: L.H.S. = (sin4 θ – cos4 θ + 1) cosec2 θ
= [(sin2 θ + cos2 θ) (sin2 θ – cos2 θ) + 1] cosec2 θ
[(1) (sin2 θ – cos2 θ) + 1] cosec2 θ as [ sin2 θ + cos2 θ = 1]
= [sin2 θ + (1 – cos2 θ)] cosec2 θ
= (sin2 θ + sin2 θ) cosec2θ
= (2 sin2 θ) cosec2 θ
= 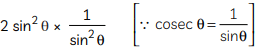
= 2 × 1
= 2 = R.H.S.
Hence, proved.
Previous Year Questions 2019
Q1: If sin x + cos y = 1, x = 30° and y is an acute angle, find the value of y. (2019) View Answer
View Answer 
Ans: Given,
⇒ sin x + cos y = 1
⇒ sin 30° + cos y = 1
⇒ 1/2 + cos y = 1
⇒ cos y = 1 - 1/2
⇒ cos y = 1/2
⇒ cos y = cos 60°.
Hence, y = 60°.
Q2: If cosec2 θ (cos θ - 1)(1 + cos θ) = k, then what is the value of k? (2019)
 View Answer
View Answer 
Ans: Given:
cosec2 θ (cos θ - 1)(1 + cos θ) = k
Concept used:
Cosec α = 1/Sin α
Sin2 α + Cos2 α = 1
(a + b)(a - b) = a2 - b2
Calculation:
cosec2 θ (cos θ - 1)(1 + cos θ) = k
⇒ cosec2 θ (1 - cos θ)(1 + cos θ) = - k
⇒ cosec2 θ (1 - cos2 θ) = -k [Also, sin2 θ + cos2 θ = 1]
⇒ cosec2 θ × sin2 θ = -k
⇒ 1 = -k
⇒ k = -1
∴ The value of k is (-1).
Q3: The value of ( 1 + cot A − cosec A ) ( 1 + tan A + sec A ) is
 View Answer
View Answer 
Ans:
(1 + cos Asin A - 1sin A ) (1 + sin Acos A + 1cos A )
= sin A + cos A - 1sin A × cos A + sin A + 1cos A
= (sin A + cos A)2 - 1sin A . cos A
= sin2A + cos2A + 2 sin A . cos A - 1sin A . cos A
= sin2A + cos2A - 1 + 2 sin A . cos Asin A . cos A
= 2
Previous Year Questions 2013
Q1: If sec θ + tan θ + 1 = 0, then sec θ – tan θ is:(a) –1
(b) 1
(c) 0
(d) 2 (CBSE 2013)
 View Answer
View Answer 
Ans: (a)
sec θ + tan θ + 1 = 0
⇒ sec θ + tan θ = -1
Multiplying and dividing LHS by sec θ - tan θ, we get
⇒ (sec θ + tan θ) × sec θ - tan θsec θ - tan θ = -1
⇒ sec² θ - tan² θsec θ - tan θ = -1
⇒ 1 + tan² θ - tan² θsec θ - tan θ = -1 (∵ sec² θ = 1 + tan² θ)
⇒ 1sec θ - tan θ = -1
⇒ sec θ - tan θ = -1
Hence, the correct option is (a).
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 8 Previous Year Questions - Introduction to Trigonometry
| 1. What are the basic trigonometric ratios? |  |
| 2. How can I remember the trigonometric identities? |  |
| 3. What is the unit circle, and why is it important in trigonometry? |  |
| 4. What are some real-world applications of trigonometry? |  |
| 5. How do I solve trigonometric equations? |  |






















