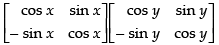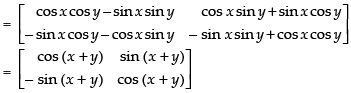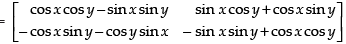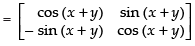Q.1. If a matrix has 28 elements, what are the possible orders it can have? What if it has 13 elements?
Ans.
The possible orders that a matrix having 28 elements are {28 × 1, 1 × 28, 2 × 14, 14 × 2, 4 × 7, 7 × 4}. The possible orders of a matrix having 13 elements are {1 × 13, 13 × 1}.
Q.2. In the matrix A = write:
write:
(i) The order of the matrix A
(ii) The number of elements
(iii) Write elements a23, a31, a12
Ans.
(i) The order of the given matrix A is 3 × 3
(ii) The number of elements in matrix A = 3 × 3 = 9
(iii) aij = the elements of ith row and jth column.
So, a23 = x2 – y, a31 = 0, a12 = 1.
Q.3. Construct a2 × 2 matrix where

(ii) aij = |−2i + 3j|
Ans.
Let
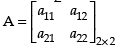
(i) Given that
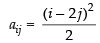
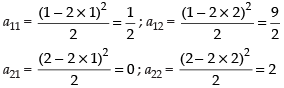
Hence, the matrix A =
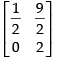
(ii) Given that
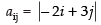
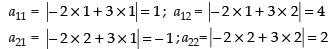
Hence, the matrix A =
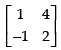
Q.4. Construct a 3 × 2 matrix whose elements are given by aij = eixsinjx
Ans. Let
Given that aij = eix sin jx
a11 = ex sin x a12 = ex sin 2x
a21 = e2x sin x a22 = e2x sin 2x
a31 = e3x sin x a32 = e3x sin 2x
Hence, the matrix
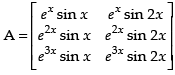
Q.5. Find values of a and b if A = B, where
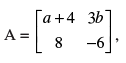
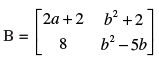
Ans.
Given that A = B
⇒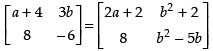
Equating the corresponding elements, we get
a + 4 = 2a + 2, 3b = b2 + 2 and b2 – 5b = – 6
⇒ 2a - a = 2, b2 - 3b + 2 = 0, b2 - 5b + 6 = 0
∴ a = 2
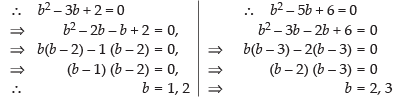
but here 2 is common.
Hence, the value of a = 2 and b = 2.
Q.6. If possible, find the sum of the matrices A and B, where A = and B =
and B =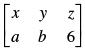
Ans.
The order of matrix A = 2 × 2 and the order of matrix B = 2 × 3 Addition of matrices is only possible when they have same order. So, A + B is not possible.
Q.7. If find
find
(i) X +Y
(ii) 2X – 3Y
(iii) A matrix Z such that X + Y + Z is a zero matrix.
Ans.
Given that
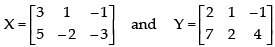
(i) X + Y =
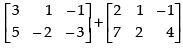
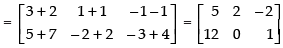
(ii) 2X – 3Y =
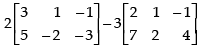
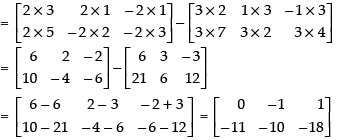
(iii) X + Y + Z = 0
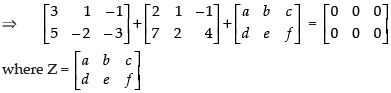

Equating the corresponding elements, we get
5 + a = 0 ⇒ a = – 5, 2 + b = 0 ⇒ b = – 2, – 2 + c = 0 ⇒ c = 2
12 + d = 0 ⇒ d = – 12, e = 0, 1 + f = 0 ⇒ f = – 1
Hence, the matrix,
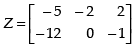
Q.8. Find non-zero values of x satisfying the matrix equation:
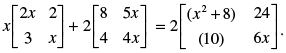
Ans.
The given equation can be written as
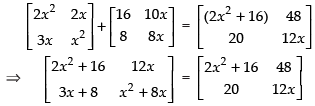
Equating the corresponding elements we get
12x = 48, 3x + 8 = 20, x2 + 8x = 12x
∴ x = 48/12 = 4, 3x = 20 – 8 = 12, ⇒ x2 = 12x – 8x = 4x
∴ x = 4, ⇒ x2 – 4x = 0 x = 0, x = 4
Hence, the non-zero values of x is 4.
Q.9. If  show that (A + B) (A – B) ≠ A2 – B2.
show that (A + B) (A – B) ≠ A2 – B2.
Ans.
Given that
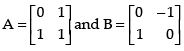
A + B =
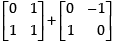
⇒ A + B =
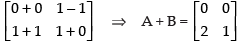
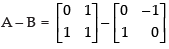
⇒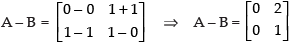
∴ (A + B) × (A - B) =
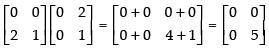
Now, R.H.S. = A2 – B2
= A × A - B × B
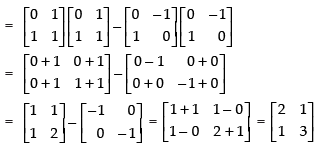
Hence,
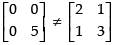
Hence, (A + B) . (A – B) ≠ A2 - B2
Q.10. Find the value of x if

Ans.
Given that,
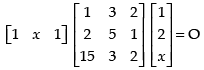
⇒ 
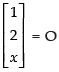
⇒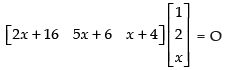
⇒ [2x + 16 + 10x + 12 + x2 + 4x] = 0; ⇒ x2 + 16x + 28 = 0
⇒ x2 + 14x + 2x + 28 = 0; ⇒ x(x + 14) + 2(x + 14) = 0
⇒ (x + 2) (x + 14) = 0; x + 2 = 0 or x + 14 = 0
∴ x = – 2 or x = – 14
Hence, the values of x are – 2 and – 14.
Q.11. Show that satisfies the equation A2 – 3A – 7I = O and hence find A–1.
satisfies the equation A2 – 3A – 7I = O and hence find A–1.
Ans.
Given that

A2 = A × A
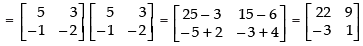
A2 – 3A – 7I = O
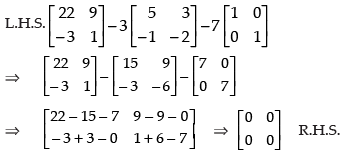
We are given A2 – 3A – 7I = O
⇒ A–1 [A2 – 3A – 7I] = A–1O
[Pre-multiplying both sides by A–1]
⇒ A–1A × A – 3A–1 × A – 7A–1 I = O [A–1O = O]
⇒ I × A – 3I – 7A–1 I = O
⇒ A – 3I – 7A–1 = O
⇒ –7A–1 = 3I – A
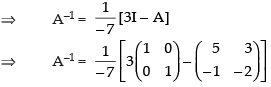
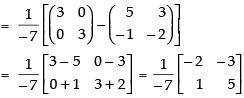
Hence,
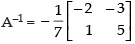
Q.12. Find the matrix A satisfying the matrix equation:

Ans.
Let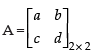
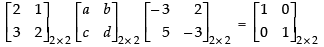
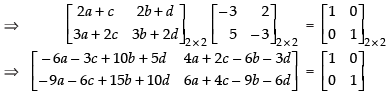
Equating the corresponding elements, we get,
– 6a – 3c + 10b + 5d = 1 ...(1)
–9a – 6c + 15b + 10d = 0 ...(2)
4a + 2c – 6b – 3d = 0 ...(3)
6a + 4c – 9b – 6d = 1 ...(4)
Multiplying eq. (1) by 2 and subtracting eq. (2), we get,
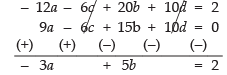
– 3a + 5b = 2 ...(5)
Now, multiplying eq. (3) by 2 and subtracting eq. (4), we get
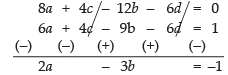
2a – 3b = – 1 ...(6)
Solving eq. (5) and (6) i.e.,
– 3a + 5b = 2
2a – 3b = – 1
2 x (- 3a + 5b = 2) ⇒ 6a + 10b = 4
3 x (2a - 3b = -1) ⇒ 6a - 9b = - 3
Adding b = 1
Putting the value of b in eq. (6), we get,
2a – 3 x 1 = - 1
⇒ 2a - 3 = - 1 ⇒ 2a = 3 - 1 ⇒ 2a = 2
∴ a = 1
Now, putting the values of a and b in equations (1) and (3)
–6 x 1 - 3c + 10 x 1 + 5d = 1
⇒ - 6 - 3c + 10 + 5d = 1
⇒ – 3c + 5d + 4 = 1 ⇒ 3c + 5d = - 3 ...(7)
and from eq. (3)
4 x 1 + 2c - 6 x 1 - 3d = 0; ⇒ 4 + 2c - 6 - 3d = 0
⇒ - 2 + 2c - 3d = 0 ⇒ 2c - 3d = 2 ...(8)
Solving eq. (7) and (8) we get,
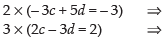

Adding
Putting the value of d in eq. (8) we get,
2c – 3 x 0 = 2 ⇒ 2c= 2 ⇒ c = 1
Hence,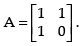
Q.13. Find A, if
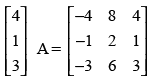
Ans.
Order of is 3 × 1 and order of
is 3 × 1 and order of is 3 x 3. So, the order of matrix A must be 1 x 3.
is 3 x 3. So, the order of matrix A must be 1 x 3.
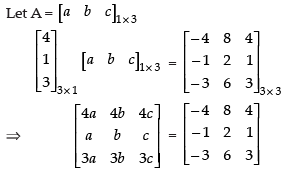
Equating the corresponding elements to get the values of a, b and c
4a = – 4, 4b = 8, 4c = 4
∴ a = – 1 ∴ b = 2 ∴ c = 1
Hence, matrix A = [- 1 2 1]
Q.14. If A = and B =
and B = then verify (BA)2 ≠ B2A2
then verify (BA)2 ≠ B2A2
Ans.
Here,

∴
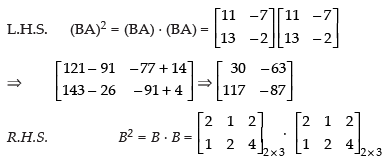
Here, number of columns of first i.e., 3 is not equal to the number of rows of second matrix i.e., 2.
So, B2 is not possible. Similarly, A2 is also not possible.
Hence, (BA)2 ≠ B2A2
Q.15. If possible, find BA and AB, where

Ans.
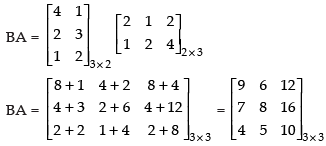
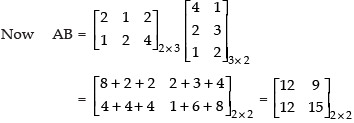
Hence,
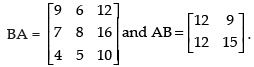
Q.16. Show by an example that for A ≠ O, B ≠ O, AB = O.
Ans.
Let

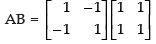
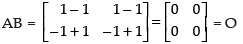
Hence,
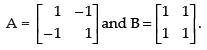
Q.17. Given  Is (AB)′ = B′A′?
Is (AB)′ = B′A′?
Ans.
Here,
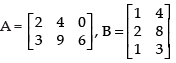
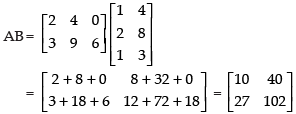
L.H.S.
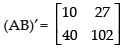
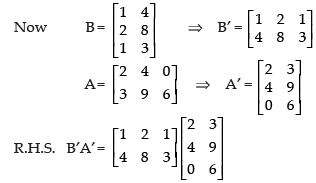

Hence, L.H.S. = R.H.S.
Q.18. Solve for x and y:

Ans.
Given that:


Comparing the corresponding elements of both sides, we get,
2x + 3y – 8 = 0 ⇒ 2x + 3y = 8 ...(1)
x + 5y – 11 = 0 ⇒ x + 5y = 11 ...(2)
Multiplying eq. (1) by 1 and eq. (2) by 2, and then on subtracting, we get,
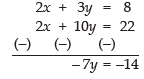
∴ y = 2
Putting y = 2 in eq. (2) we get,
x + 5 x 2 = 11 ⇒ x + 10 = 11
∴ x = 11 – 10 = 1
Hence, the values of x and y are 1 and 2 respectively.
Q.19. If X and Y are 2 × 2 matrices, then solve the following matrix equations for X and Y
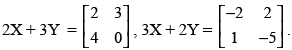
Ans.
Given that:
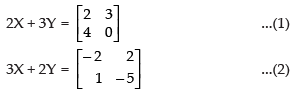
Multiplying eq. (1) by 3 and eq. (2) by 2, we get,
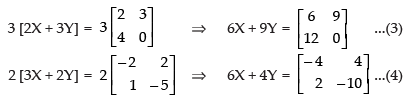
On subtracting eq. (4) from eq. (3) we get
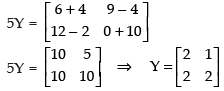
Now, putting the value of Y in equation (1) we get,
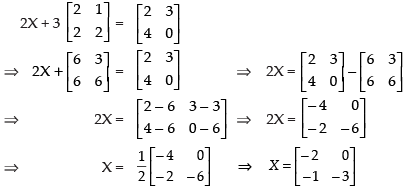
Hence,
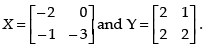
Q.20. If A = [3 5], B = [7 3], then find a non-zero matrix C such that AC = BC.
Ans.
Given that:
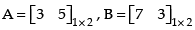
Let,
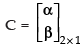
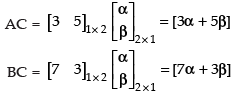
AC = BC (Given)
⇒ [3α + 5β] = [7α + 3β]
⇒ 3α + 5β = 7α + 3β
⇒ 3α – 7α = 3β – 5β
⇒ – 4α = – 2β
∴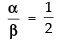
So, let α = K and β = 2K, K is some real number.
Hence, matrix C =
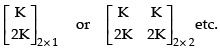
Q.21. Give an example of matrices A, B and C such that AB = AC, where A is nonzero matrix, but B ≠ C.
Ans.
Let,
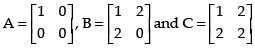
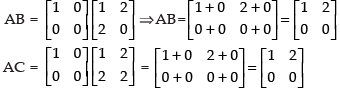
Hence, AB = AC for matrix A is non-zero and B ≠ C.
Q.22. If
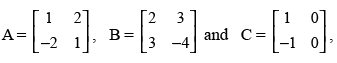
(i) (AB) C = A (BC)
(ii) A (B + C) = AB + AC.
Ans.
Given that
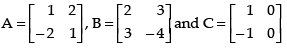
(i) To verify: (AB)C = A(BC)

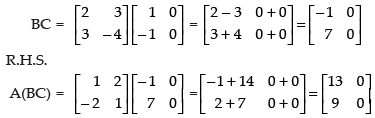
L.H.S. = R.H.S.
So, (AB)C = A(BC)
(ii) To verify: A(B + C) = AB + AC
L.H.S. B + C
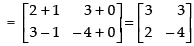
L.H.S.A(B + C) 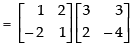
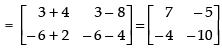
R.H.S. AB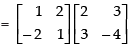
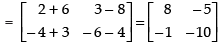
AC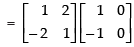
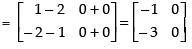
R.H.S. AB + AC
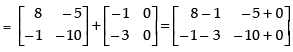
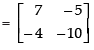
L.H.S. = R.H.S.
Hence, A(B + C) = AB + AC
Q.23. If
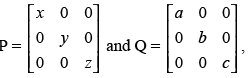
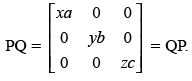
Ans.
Given that:
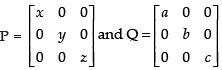
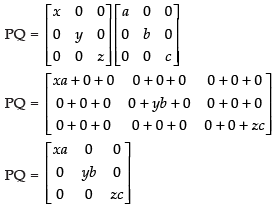
Now
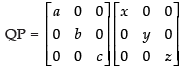

Hence, PQ = QP.
Q.24. If : find A.
find A.
Ans.
Given that:
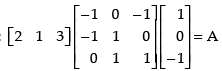
L.H.S.
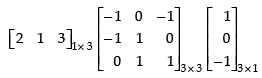
⇒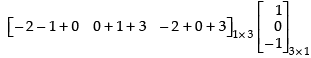
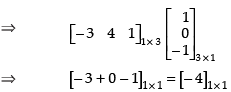
Hence, matrix A = [– 4]
Q.25. If A = [ 2 1] , B = verify that A (B + C) = (AB + AC).
verify that A (B + C) = (AB + AC).
Ans.
Given that:
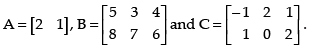
L.H.S.
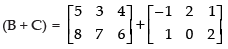

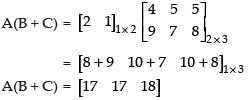
R.H.S.
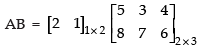
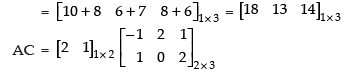
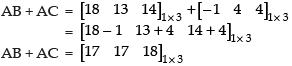
L.H.S. = R.H.S.
Hence, A(B + C) = (AB + AC) is verified.
Q.26. If  then verify that A2 + A = A (A + I), where I is 3 × 3 unit matrix.
then verify that A2 + A = A (A + I), where I is 3 × 3 unit matrix.
Ans.
Given that:
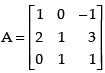
A2 = A × A
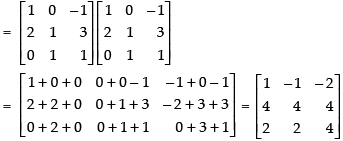
L.H.S. A2 + A =

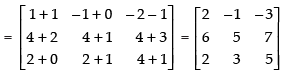
R.H.S. A(A + I) =
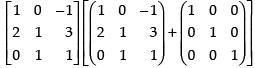
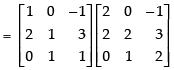
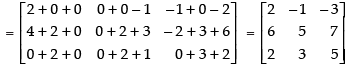
L.H.S. = R.H.S.
A2 + A = A(A + I). Hence verified.
Q.27. If  then verify that :
then verify that :
(i) (A′)′ = A
(ii) (AB)′ = B′A′
(iii) (kA)′ = (kA′).
Ans.
Given that:
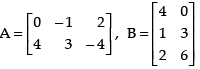
(i)
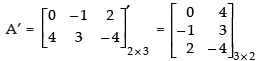
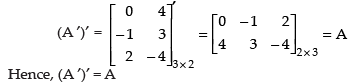
(ii) L.H.S.
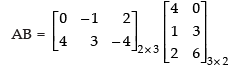
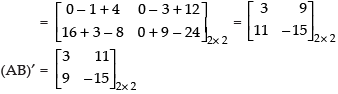
R.H.S.
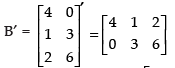
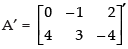
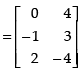
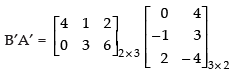

L.H.S. = R.H.S.
Hence,(AB)′ = B′A′is verified.
(iii) L.H.S.
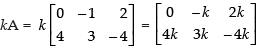
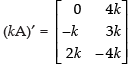
R.H.S.
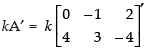
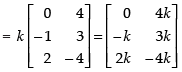
Hence, L.H.S. = R.H.S.
(kA)′ = (kA′) is verified.
Q.28. If  then verify that:
then verify that:
(i) (2A + B)′ = 2A′ + B′
(ii) (A – B)′ = A′ – B′.
Ans.
Given that:
(i) To verify that:(2A + B)′ = 2A′ + B′
L.H.S. (2A + B)′ =
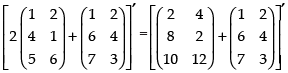
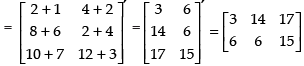
R.H.S. 2A′ + B′ =
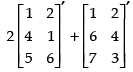
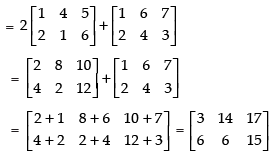
Hence, L.H.S. = R.H.S.
(2A + B)′ = 2A′ + B′is verified.
(ii) To verify that:(A – B)′ = A′ – B′.
L.H.S. (A – B)′ =
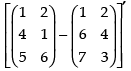
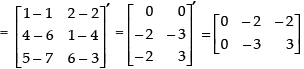
R.H.S.A′ – B′=
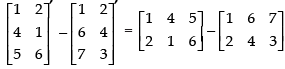

Hence, L.H.S. = R.H.S.
(A – B)′ = A′ – B′ is verified.
Q.29. Show that A′A and AA′ are both symmetric matrices for any matrix A.
Ans.
Let P = A′A
⇒ P′ = (A′A)′
⇒ P′ = A′(A′)′ [(AB)′ = B′A′]
⇒ P′ = A′A [∵ (A′)′ = A]
⇒ P′ = P
Hence, A¢A is a symmetric matrix.
Now, Let Q = AA′
⇒ Q′ = (AA′)′
⇒ Q′ = (A′)′ A′ [(AB)′ = B′A′]
⇒ Q′ = AA′ [∵ (A′)′ = A]
⇒ Q′ = Q
Hence, AA′ is also a symmetric matrix.
Q.30. Let A and B be square matrices of the order 3 × 3. Is (AB)2 = A2 B2 ? Give reasons.
Ans.
Given that A and B are the matrices of the order 3 x 3.
(AB)2 = AB × AB
= AA × BB
= A2 × B2
Hence, (AB)2 = A2B2
Q.31. how that if A and B are square matrices such that AB = BA, then
(A + B)2 = A2 + 2AB + B2.
Ans.
To prove that (A + B)2 = A2 + 2AB + B2
L.H.S. (A + B)2 = (A + B) × (A + B) [∵ A2 = A × A]
= A × A + AB + BA + B × B
= A2 + AB + AB + B2 [AB = BA]
= A2 + 2AB + B2 R.H.S.
So, L.H.S. = R.H.S.
Q.32. Let  and a = 4, b = –2.
and a = 4, b = –2.
Show that:
(a) A + (B + C) = (A + B) + C
(b) A (BC) = (AB) C
(c) (a + b)B = aB + bB
(d) a (C–A) = aC – aA
(e) (AT)T = A
(f) (bA)T = b AT
(g) (AB)T = BT AT
(h) (A –B)C = AC – BC
(i) (A – B)T = AT – BT
Ans.
(a) To prove that: A + (B + C) = (A + B) + C
L.H.S. A + (B + C) =
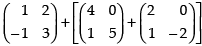
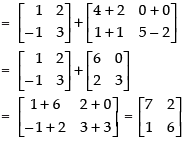
R.H.S. (A + B) + C
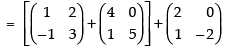
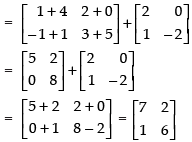
Hence, L.H.S. = R.H.S.
A + (B + C) = (A + B) + C Hence proved.
(b) To prove that: A(BC) = (AB)C
L.H.S. A(BC) =
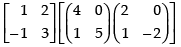
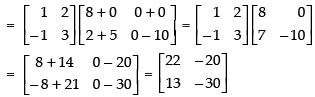
R.H.S. (AB)C
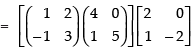
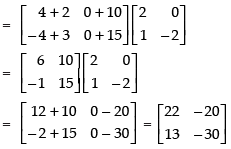
Hence, L.H.S. = R.H.S.
A(BC) = (AB)C Hence proved.
(c) To prove that: (a + b)B = aB + bB
Here, a = 4 and b = – 2
L.H.S. (a + b)B =
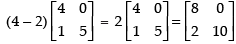
R.H.S. aB + bB
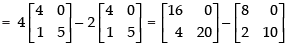
Hence, L.H.S. = R.H.S.
(a + b)B = aB + bB Hence proved.
(d) To prove that: a(C – A) = aC – aA
L.H.S. a(C – A) =
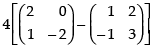

R.H.S. aC – aA =
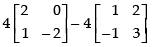
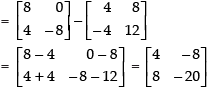
Hence, L.H.S. = R.H.S.
a(C – A) = aC – aA Hence proved.
(e) To prove that: (AT)T = A
L.H.S.

 R.H.S.
R.H.S.
Hence, (AT)T = A
(f) To prove that: (bA)T = bAT
L.H.S. (bA)T =
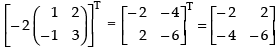
R.H.S. bAT =
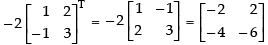
Hence, L.H.S. = R.H.S.
(bA)T = bAT Hence proved.
(g) To prove that: (AB)T = BTAT
L.H.S. (AB)T
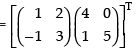
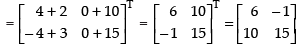
R.H.S. BTAT=

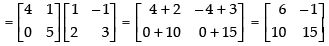
Hence, L.H.S. = R.H.S.
(AB)T = BTAT Hence proved.
(h) To prove that: (A – B)C = AC – BC
L.H.S. (A – B)C =
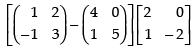

R.H.S. AC – BC =
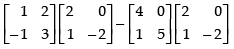

Hence, L.H.S. = R.H.S.
(A – B)C = AC – BC
(i) To prove that: (A – B)T = AT – BT
L.H.S. (A – B)T =
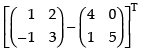
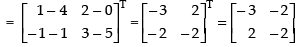
R.H.S. AT – BT =

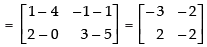
Hence, L.H.S. = R.H.S.
(A – B)T = AT – BT Hence proved.
Q.33. If A = then show that A2 =
then show that A2 =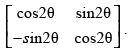
Ans. Given that
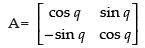
A = A . A=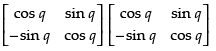
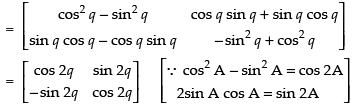
Hence proved.
Q.34. If A = and x2 = –1, then show that (A + B)2 = A2 + B2.
and x2 = –1, then show that (A + B)2 = A2 + B2.
Ans. Given that:
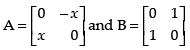
L.H.S. (A + B)2 = (A + B) × (A + B)
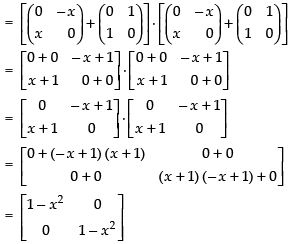
Put x2 = –1 (given)
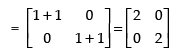
R.H.S.
A2 + B2 = A × A + B × B
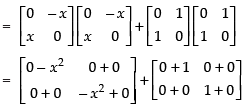
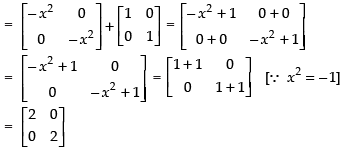
Hence, L.H.S. = R.H.S.
(A + B)2 = A2 + B2
Q.35. Verify that A2 = I when A =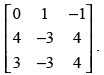
Ans. Given that:
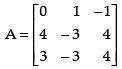
L.H.S. A2 = A × A =
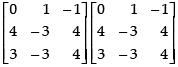
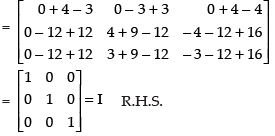
Hence, A2 = I is verified.
Q.36. Prove by Mathematical Induction that (A′)″ = (A″)′, where n ∈ N for any square matrix A.
Ans.
To prove that (A′)″ = (A″)′
Let P (n): (A′)″ = (A″)′
Step 1: Put n = 1, P(1): A′ = A′ which is true for n = 1
Step 2: Put n = K, P(K): (A′)K = (AK)′ Let it be true for n = K
Step 3: Put n = K + 1, P(K + 1): (A′)K + 1 = (AK + 1)′
L.H.S. (A′)K + 1 = (A′)K × (A′)
= (AK)′ × (A′) (From step 2)
= (AK × A)′
= (AK+1)′ R.H.S.
The given statement is true for P(K+1) whenever it is true for P(K), where K ∈ N.
Q.37. Find inverse, by elementary row operations (if possible), of the following matrices
(i)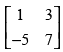
(ii)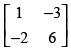
Ans.
(i) Let
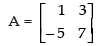
|A| = 1 x 7 - (- 5) x 3 = 7 + 15 = 22 ≠ 0
So, A is invertible.
Let A = IA
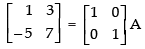
R2 → R2 + 5R1
⇒ 
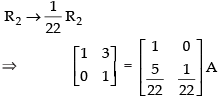
R1 → R1 - 3R2
⇒ =
=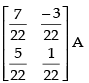
So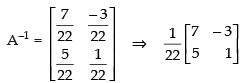
Hence, inverse of 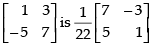
(ii) Let
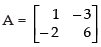
|A| = 1 x 6 - (- 3) (- 2) = 6 - 6 = 0
|A| = 0 so A is not invertible.
Hence, inverse of is not possible.
is not possible.
Q.38. If then find values of x, y, z and w.
then find values of x, y, z and w.
Ans.
Given that:
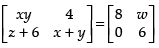
Equating the corresponding elements,
xy = 8, w = 4, z + 6 = 0 ⇒ z = – 6, x + y = 6
Now, solving x + y = 6 ...(i)
and xy = 8 ...(ii)
From eqn. (i), y = 6 – x ...(iii)
Putting the value of y in eqn. (ii) we get,
x(6 – x) = 8 ⇒ 6x – x2 = 8
⇒ x2 – 6x + 8 = 0 ⇒ x2 – 4x – 2x + 8 = 0
⇒ x(x – 4) – 2(x – 4) = 0 ⇒ (x - 4) (x - 2) = 0
∴ x = 4, 2
From eqn. (iii), y = 2, 4.
Hence, x = 4 or 2, y = 2 or 4, z = – 6 and w = 4.
Q.39. If find a matrix C such that 3A + 5B + 2C is a null matrix.
find a matrix C such that 3A + 5B + 2C is a null matrix.
Ans.
Order of matrices A and B is 2 × 2.
∴ Order of matrix C must be 2 × 2.
Let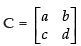
∴ 3A + 5B + 2C = 0
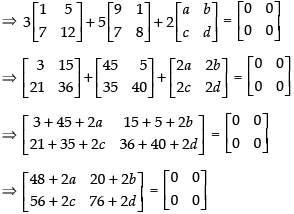
Equating the corresponding elements, we get,
48 + 2a = 0 ⇒ 2a = - 48 ⇒ a = - 24
20 + 2b = 0 ⇒ 2b = - 20 ⇒ b = - 10
56 + 2c = 0 ⇒ 2c = - 56 ⇒ c = - 28
76 + 2d = 0 ⇒ 2d = - 76 ⇒ d = - 38
Hence,
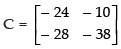
Q.40. If A = then find A2 – 5A – 14I. Hence, obtain A3.
then find A2 – 5A – 14I. Hence, obtain A3.
Ans.
Given that:
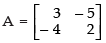
A2 = A . A =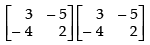
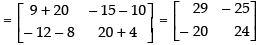
∴ A2 – 5A – 14I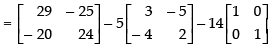
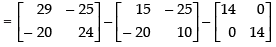

Hence, A2 – 5A – 14I = O
Now, multiplying both sides by A, we get,
A2 . A – 5A . A – 14IA = OA
⇒ A3 – 5A2 – 14A = 0
⇒ A3 = 5A2 + 14A
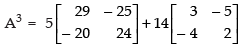
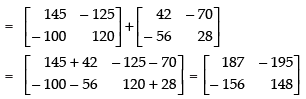
Hence, A3 =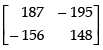
Q.41. Find the values of a, b, c and d, if
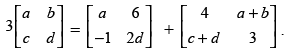
Ans.
Given that:
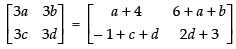
Equating the corresponding elements, we get,
3a = a + 4 ⇒ 3a – a = 4 ⇒ 2a = 4 ⇒ a = 2
3b = 6 + a + b ⇒ 3b – b – a = 6 ⇒ 2b – a = 6 ⇒ 2b – 2 = 6
⇒ 2b = 8
⇒ b = 4 3c = – 1 + c + d
⇒ 3c – c – d = – 1 ⇒ 2c – d = – 1
and 3d = 2d + 3 ⇒ 3d – 2d = 3 ⇒ d = 3
Now 2c – d = – 1
⇒ 2c – 3 = – 1 ⇒ 2c = 3 - 1 ⇒ 2c = 2
∴ c = 1
∴ a = 2, b = 4, c = 1 and d = 3.
Q.42. Find the matrix A such that
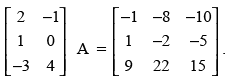
Ans.
Order of matrix  is 3 × 2 and the matrix
is 3 × 2 and the matrix
 is 3 × 3
is 3 × 3
∴ Order of matrix A must be 2 × 3
Let A =

So,
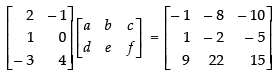
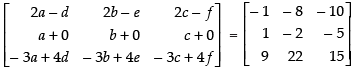
Equating the corresponding elements, we get,
2a – d = – 1 and a = 1 ⇒ 2 × 1 – d = – 1 ⇒ d = 2 + 1 ⇒ d = 3
2b – e = – 8 and b = – 2 ⇒ 2(– 2) – e = – 8 ⇒ – 4 – e = – 8
⇒ e = 4
2c – f = – 10 and c = – 5 ⇒ 2(– 5) – f = – 10 ⇒ – 10 – f = – 10
⇒ f = 0
a = 1, b = – 2, c = – 5, d = 3, e = 4 and f = 0
Hence,
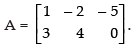
Q.43. If A = find A2 + 2A + 7I.
find A2 + 2A + 7I.
Ans.
Given that:
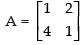
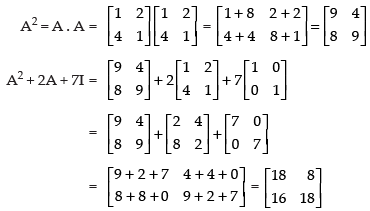
Hence, A2 + 2A + 7I =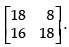
Q.44. If A = and A –1 = A′ , find value of α.
and A –1 = A′ , find value of α.
Ans.
Here,
A=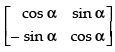
Given that: A– 1 = A′
Pre-multiplying both sides by
AA– 1 = AA′
⇒ I = AA′ [∵ AA-1 = I]
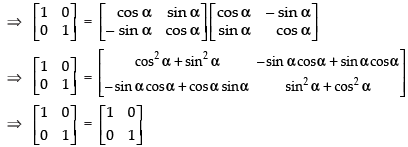
Hence, it is true for all values of α.
Q.45. If the matrix is a skew symmetric matrix, find the values of a, b and c.
is a skew symmetric matrix, find the values of a, b and c.
Ans.
Let,
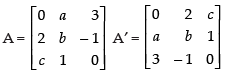
For skew symmetric matrix, A′ = - A.
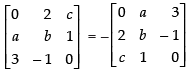
⇒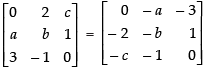
Equating the corresponding elements, we get
a = – 2, b = – b ⇒ 2b = 0 ⇒ b = 0 and c = - 3
Hence, a = - 2, b = 0 and c = - 3.
Q.46. If P (x) = then show that
then show that
P(x) . P(y) = P(x + y) = P(y) . P(x).
Ans.
Given that:
 [Replacing x by y]
[Replacing x by y]
P(x).P(y)
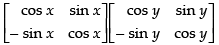
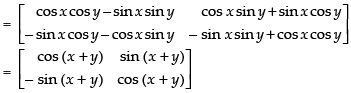
P(x + y)
Now
P(y).P(x)

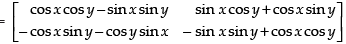
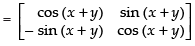
= P(x + y)
Hence, P(x).P(y) = P(x + y) = P(y).P(x).
Q.47. If A is square matrix such that A2 = A, show that (I + A)3 = 7A + I.
Ans.
To show that: (I + A)3 = 7A + I
L.H.S. (I + A)3 = I3 + A3 + 3I2A + 3IA2
⇒ I + A2.A + 3IA + 3IA2
⇒ I + A.A + 3IA + 3IA [∵ A2 = A]
⇒ I + A2 + 3IA + 3IA
⇒ I + A + 3IA + 3IA [∵ A2 = A]
⇒ I + A + 3A + 3A ⇒ 7A + I R.H.S.
L.H.S. = R.H.S. Hence, Proved.
Q.48. If A, B are square matrices of same order and B is a skew-symmetric matrix, show that A′BA is skew symmetric.
Ans.
Given that B is a skew symmetric matrix
∴ B′ = - B
Let P = A′BA
⇒ P′ = (A′BA)′
= A′B′(A′)′ [(AB)′ = B′A′]
= A′(- B) A
= – A′BA = - P
So P′ = – P
Hence, A′BA is a skew symmetric matrix.
 write:
write:
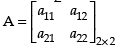
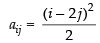
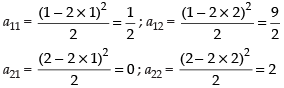

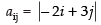
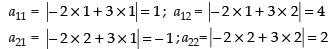
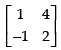

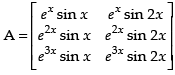
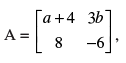
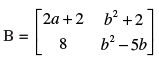
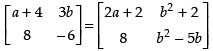
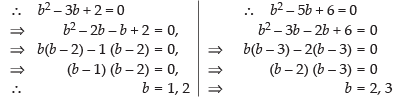
 and B =
and B =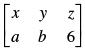
 find
find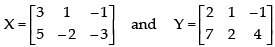
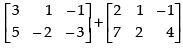
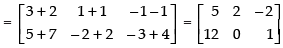
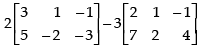
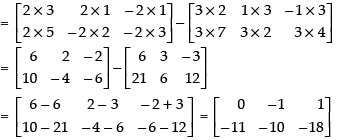
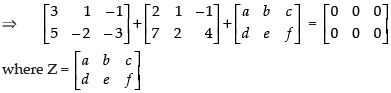

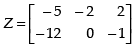
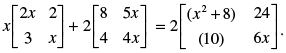
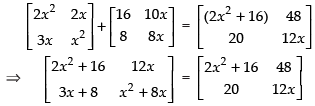
 show that (A + B) (A – B) ≠ A2 – B2.
show that (A + B) (A – B) ≠ A2 – B2.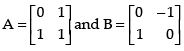
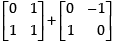
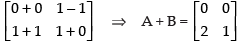
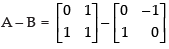
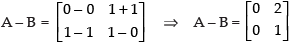
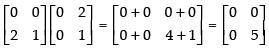
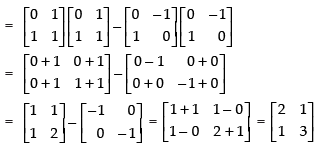
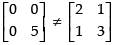

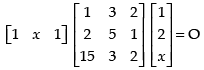

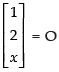
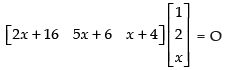
 satisfies the equation A2 – 3A – 7I = O and hence find A–1.
satisfies the equation A2 – 3A – 7I = O and hence find A–1.
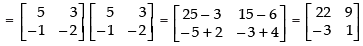
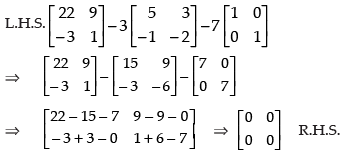
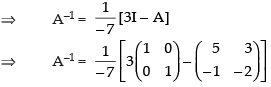
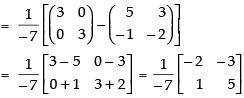
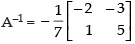

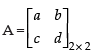
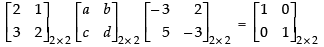
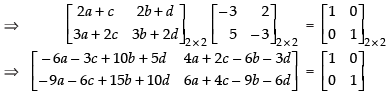
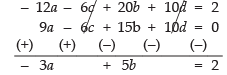
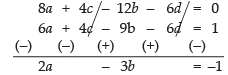
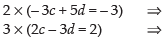

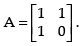
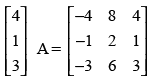
 is 3 × 1 and order of
is 3 × 1 and order of is 3 x 3. So, the order of matrix A must be 1 x 3.
is 3 x 3. So, the order of matrix A must be 1 x 3.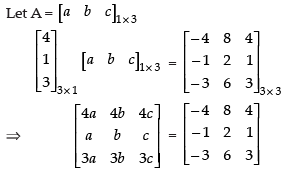
 and B =
and B = then verify (BA)2 ≠ B2A2
then verify (BA)2 ≠ B2A2

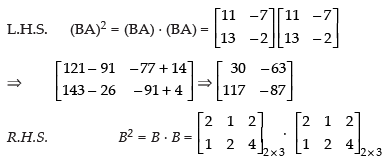

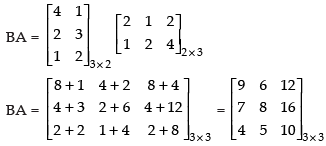
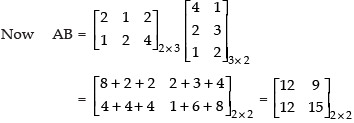
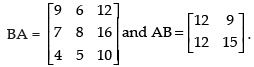

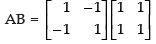
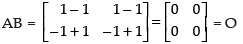
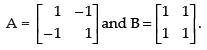
 Is (AB)′ = B′A′?
Is (AB)′ = B′A′?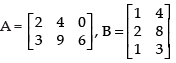
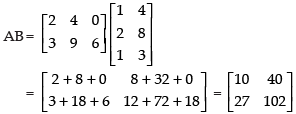
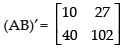
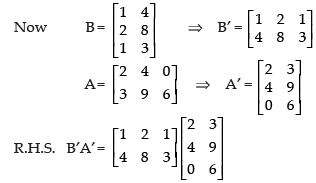




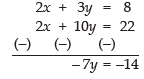
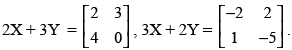
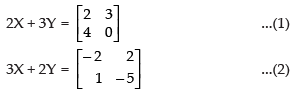
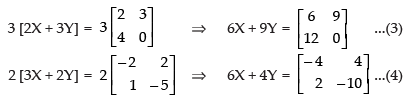
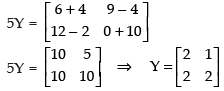
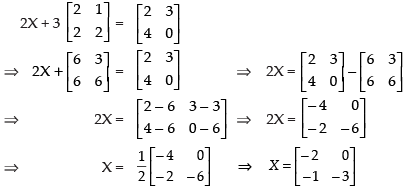
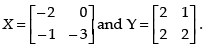
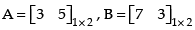
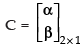
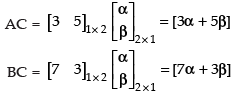
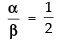
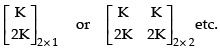
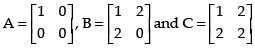
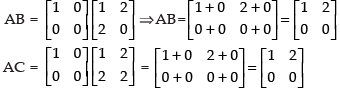
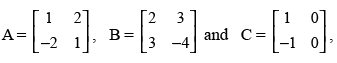
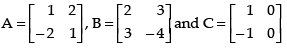

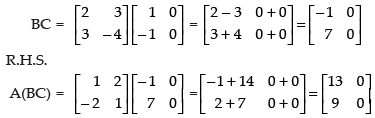

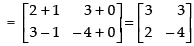
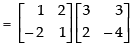
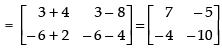
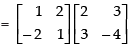
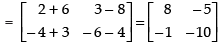
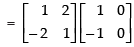
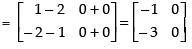
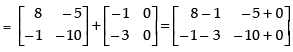
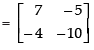
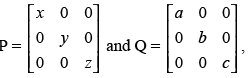
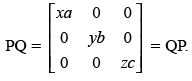
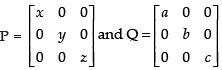
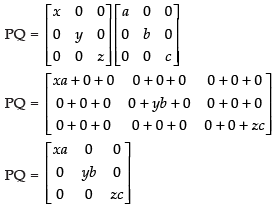
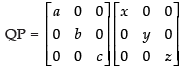

 find A.
find A.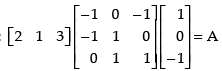
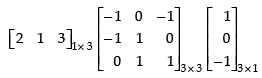
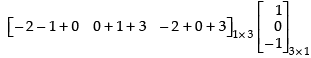
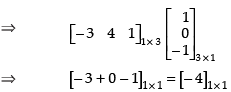
 verify that A (B + C) = (AB + AC).
verify that A (B + C) = (AB + AC).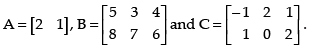
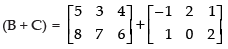

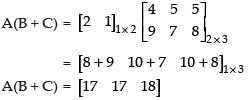
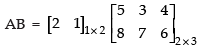
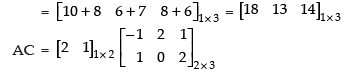
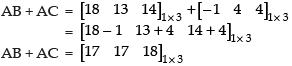
 then verify that A2 + A = A (A + I), where I is 3 × 3 unit matrix.
then verify that A2 + A = A (A + I), where I is 3 × 3 unit matrix.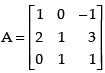
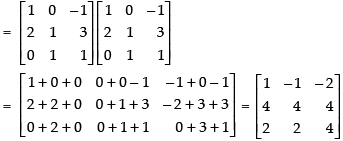

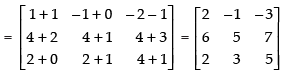
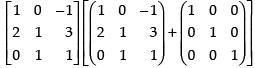
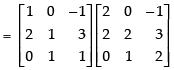
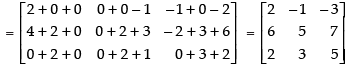
 then verify that :
then verify that :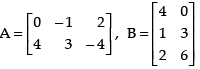
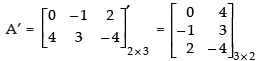
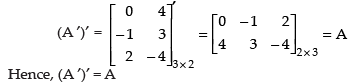
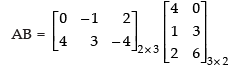
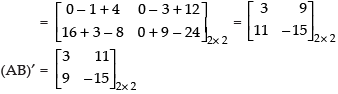
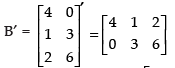
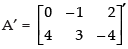
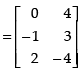
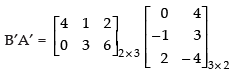

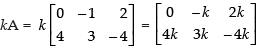
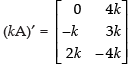
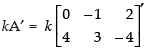
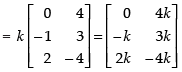
 then verify that:
then verify that: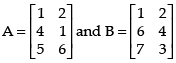
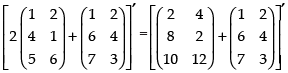
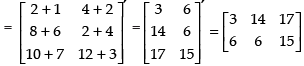
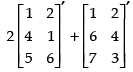
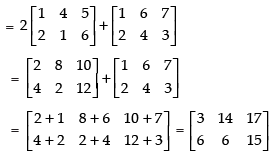
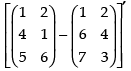
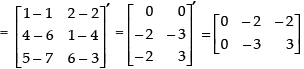
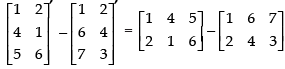

 and a = 4, b = –2.
and a = 4, b = –2.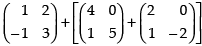
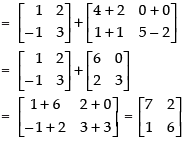
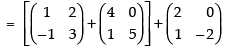
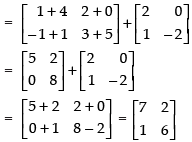
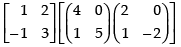
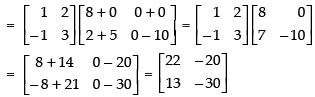
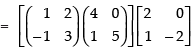
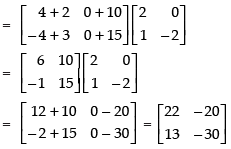
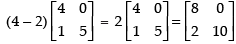
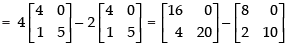
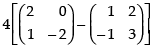

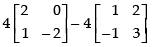
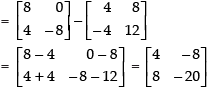

 R.H.S.
R.H.S.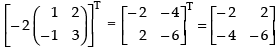
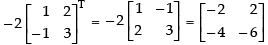
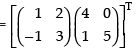
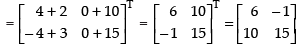

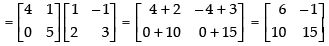
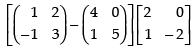

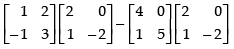

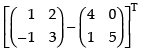
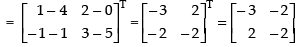

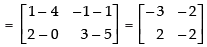
 then show that A2 =
then show that A2 =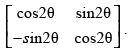
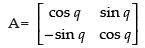
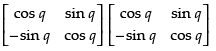
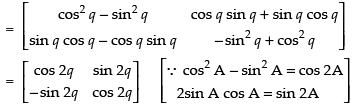
 and x2 = –1, then show that (A + B)2 = A2 + B2.
and x2 = –1, then show that (A + B)2 = A2 + B2.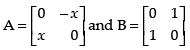
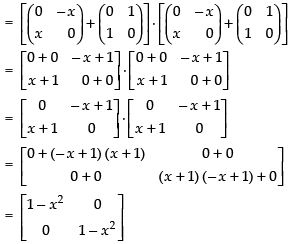
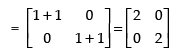
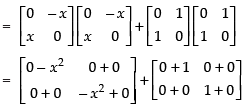
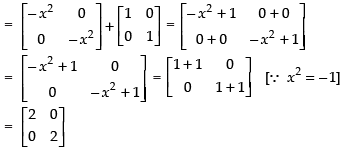
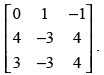
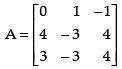
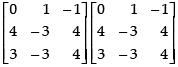
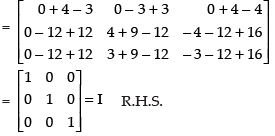
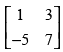
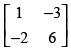
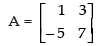
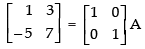

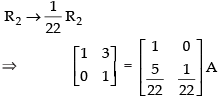
 =
=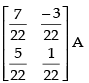
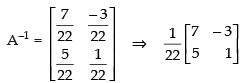
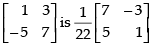
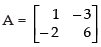
 is not possible.
is not possible. then find values of x, y, z and w.
then find values of x, y, z and w.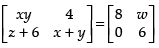
 find a matrix C such that 3A + 5B + 2C is a null matrix.
find a matrix C such that 3A + 5B + 2C is a null matrix.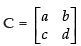
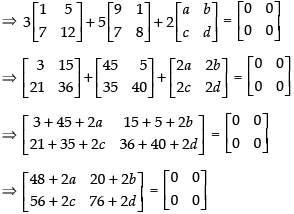
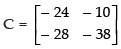
 then find A2 – 5A – 14I. Hence, obtain A3.
then find A2 – 5A – 14I. Hence, obtain A3.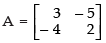
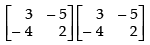
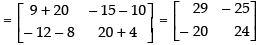
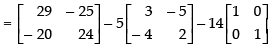
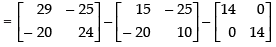

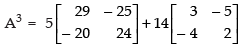
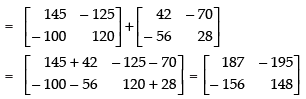
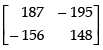
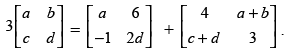

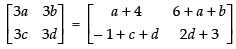
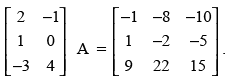
 is 3 × 2 and the matrix
is 3 × 2 and the matrix is 3 × 3
is 3 × 3
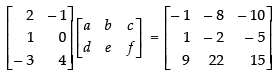
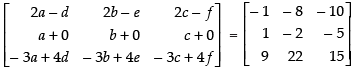
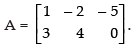
 find A2 + 2A + 7I.
find A2 + 2A + 7I.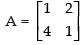
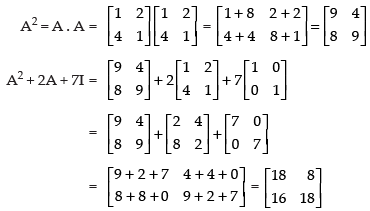
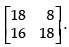
 and A –1 = A′ , find value of α.
and A –1 = A′ , find value of α.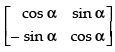
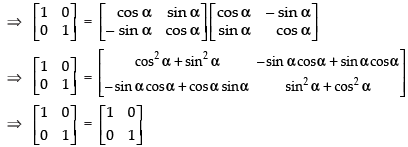
 is a skew symmetric matrix, find the values of a, b and c.
is a skew symmetric matrix, find the values of a, b and c.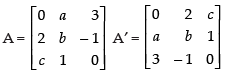
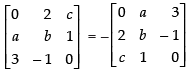
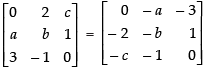
 then show that
then show that  [Replacing x by y]
[Replacing x by y]