Question for CAT Past Year Questions: HCF & LCM
Try yourself:The number of common terms in the two sequences: 15, 19, 23, 27, . . . . , 415 and 14, 19, 24, 29, . . . , 464 is?
[2019]
Explanation
Both the given sequences are A.P.
The common difference for the first sequence, d1 = 4
The common difference for the second sequence, d2 = 5
The first common term in the two given A.P. is 19.
The common terms will also be in arithmetic progression with common difference
LCM (d1, d2) = LCM (4, 5) = 20
Let there be ‘n’ terms in this sequence, then the last term would be ≤ 415
Hence for A.P. of common terms
a + (n – 1) d ≤ 415
⇒ 19 + (n – 1) × 20 ≤ 415
⇒ (n – 1) × 20 ≤ 396
⇒ (n – 1) = [396 / 20] where [396 / 20] is the greatest integer
⇒ (n –1) = 19
∴ n = 20
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:A natural number n is such that 120 ≤ n ≤ 240. If HCF of n and 240 is 1, how many values of n are possible?
[2016]
Explanation
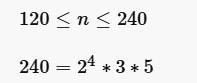
Since HCF of 240 and n is 1, it means n has none of 2, 3 and 5. 120 has 2, 3 and 5 as factors. 120 to 239 are 120 integers.
Of these 120 integers, half will have 2 as a factor so ignore those. We are left with 60 integers.
1/3 will have 3 as factor which means 40 will have 3 as factor. Of these, half will be even and half odd. We have already removed the even integers. So we remove another 20 integers only. Now we are left with 60 - 20 = 40 integers.
1/5 will have 5 as factor which means 24 integers. Of these, half will be even so they have already been removed. We are left with 12 integers. Of these, a third will have 3 as factor so they have already been removed too. We are left with 8 integers.
40 - 8 = 32 integers will have no 2, no 3 and no 5.
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:How many ordered triplets (a, b, c) exist such that LCM (a, b) = 1000, LCM (b, c) = 2000, LCM (c, a) = 2000 and HCF (a, b) = k × 125?
[2015]
Explanation
1000 = 23 × 53 and 2000 = 24 × 53
Since LCM (c, a) and LCM (b, c) is 24 × 53 and LCM (a, b) = 23 × 53, so the factor 24 must be present in c.
Hence c = 24 × 5x, where x ranges from 0 to 3 Therefore, there are four possible values of C.
Since, HCF of (a, b) = K × 53, it means
a = 2y × 53
b = 2z × 53
x = 0 to 3, y = 0, then z = 3 → 4 cases.
x = 0 to 3, y = 1, then z = 3 → 4 cases.
x = 0 to 3, y = 2, then z = 3 → 4 cases.
x = 0 to 3, y = 3, then z = 3 → 4 cases.
x = 0 to 3, y = 3, then z = 2 → 4 cases.
x = 0 to 3, y = 3, then z = 1 → 4 cases.
x = 0 to 3, y = 3, then z = 0 → 4 cases.
Hence, total cases = 28.
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:The ratio of two numbers whose sum is 600 is 7 : 8. What is the LCM of the given two numbers?
[2014]
Explanation
Let the two numbers be x and y according to question,
x + y = 600 and x/y = 7/8
∵ x + y = 600 ...(i)
x/y = 7/8 ⇒ 8x - 7y = 0 .....(ii)
From equation (i) and (ii)
x = 280 and y = 320
∴ LCM of 280 and 320 = 2240
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:How many natural numbers divide exactly one out of 1080 and 1800, but not both?
[2013]
Explanation
1080 = 23 × 33 × 51
(where N = apbqcr
∴ No. of factors (p + 1) (q + 1) (r + 1)
∴ No. of factors of 1080 (3 + 1) (3 + 1) (1 + 1) = 4 × 4 × 2 = 32
1800 = 23 × 32 × 52
(where N = apbqcr
∴ No. of factor (p + 1) (q + 1) (r + 1)
∴ Number of factor of 1800 = (3 + 1)(2 + 1)(2 +1)
= 4 × 3 × 3 = 36
∴ HCF of 1080 and 1800 = 23 × 32 × 5
where N = ap, bq, cr
No. of factors HCl = (p + 1)(q + 1)(r +1)
∴ No. of factors HCF of two numbers = (3 + 1) (2 + 1) (1 + 1)
= 4 × 3 × 2 = 24
So, the required number of divisors
= (32 + 36) – 2 × 24 = 20
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:Arrange the numbers 27/6, 33/4 and 52/3 in ascending order.
[2013]
Explanation
LCM of 6, 4 and 3 = 12
Multiply by 12 of each number in power
⇒ 214, 39, 58
So, ascending order is
58 > 39 > 214 or 52/3 > 33/4 >27/6
Report a problem
Question for CAT Past Year Questions: HCF & LCM
Try yourself:(X + 3)/3, (X + 8)/4, (X + 15)/5, (X + 24)/6 ... ((X + 80)/10 is a sequence where X ≠ 1 What is the least value of X for which HCF (Numerator, Denominator) = 1 for each term of the given sequence?
[2011]
Explanation
The general term is of the form
(X + n(n + 2)) / (n + 2)
n(n + 2) is always divisible by (n + 2).
So we can say that n(n + 2) ± 1 would never be divisible by (n + 2).
If we put X = –1, the numerator and denominator of all the terms would be co-prime.
Report a problem