RS Aggarwal Solutions: Exercise 1G - Number System | Extra Documents & Tests for Class 9 PDF Download
Q.1. Simplify
(i) 
(ii) 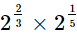
(iii) 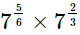
(iv) 
Ans.
(i) 
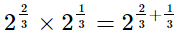
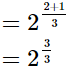
=21
= 2
(ii) 
(iii)
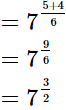
(iv) 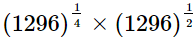
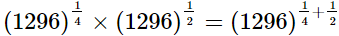
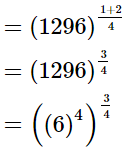
= (6)3
= 216
Q.2. Simplify:
(i)
(ii)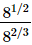
(iii)
Ans.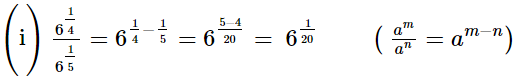
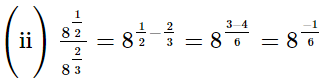
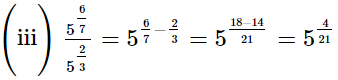
Q.3. Simplify:
(i) 31/4 × 51/4
(ii) 25/8 × 35/8
(iii) 61/2 × 71/2
Ans.
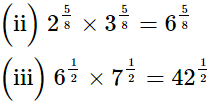
Q.4. Simplify:
(i) (34)1/4
(ii) (31/3)4
(iii) 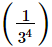
Ans.
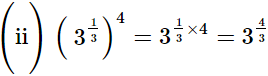
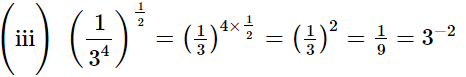
Q.5. Evaluate
(i)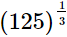
(ii)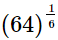
(iii)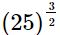
(iv)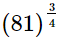
(v)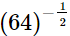
(vi)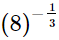
Ans.
(i) 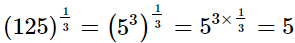
(ii)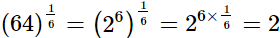
(iii)
(iv)
(v)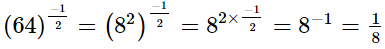
(vi)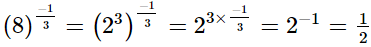
Q.6. If a = 2, b = 3, find the values of
(i) (ab + ba)–1
(ii) (aa + bb)–1
Ans.
(i) (ab + ba)–1
(ab + ba) −1 = (23 + 32) −1
= (8 + 9)−1
= (17)−1
= 1/17
(ii) (aa + bb)–1
(aa + bb)−1 = (22 + 33)−1
= (4 + 27)−1
= (31)−1
=1/31
Q.7. Simplify
(i)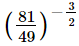
(ii) (14641)0.25
(iii)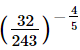
(iv)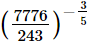
Ans.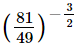
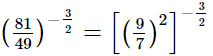
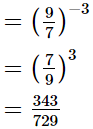
(ii) (14641)0.25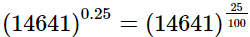
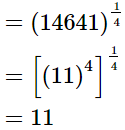
(iii) 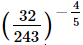
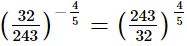
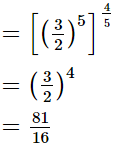
(iv)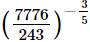
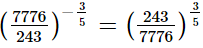
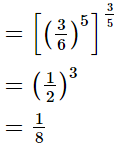
Q.8. Evaluate
(i) 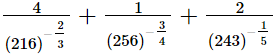
(ii) 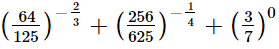
(iii) 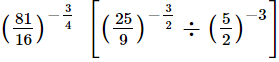
(iv) 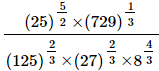
Ans.
(i)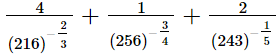
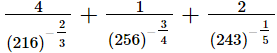
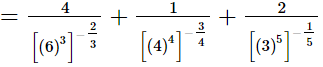
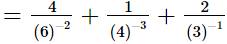
=4(6)2 + (4)3 + 2(3)
=144 + 64 + 6
=214
(ii) 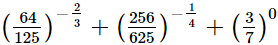
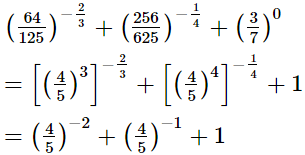

(iii) 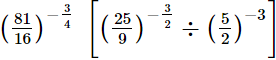
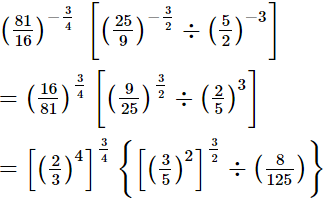
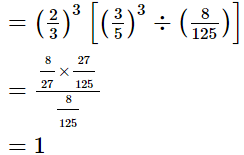
(iv) 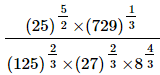
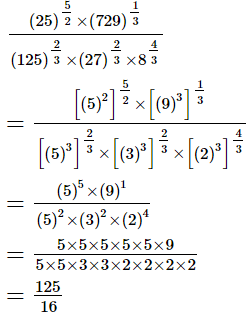
Q.9. Evaluate
(i)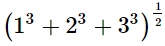
(ii)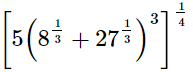
(iii) 
(iv) 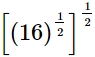
Ans.
(i) 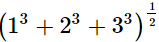
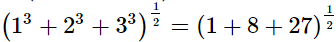
(ii) 
(iii) 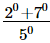
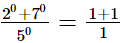
= 2
(iv) 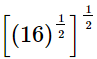
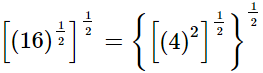
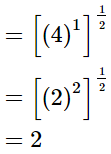
Q.10. Prove that
(i) 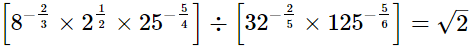
(ii) 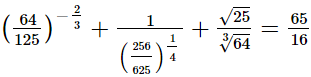
(iii) 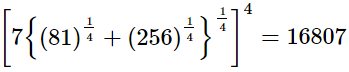
Ans.
(i) 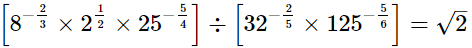
LHS = 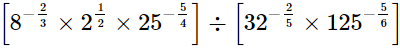

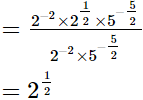
= √2
= RHS
∴ 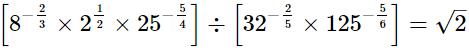
(ii) 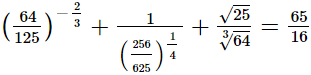
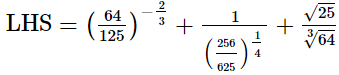

= RHS
∴
(iii) 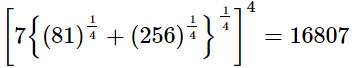
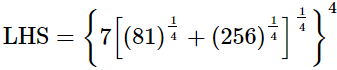
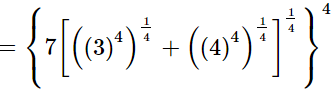
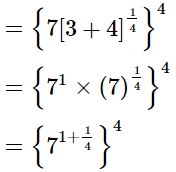
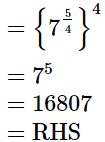
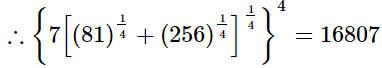
Q.11. Simplify 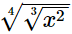 and express the result in the exponential form of x.
and express the result in the exponential form of x.
Ans.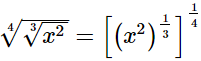
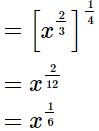
Hence, the result in the exponential form is 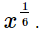
Q.12. Simplify the product 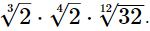
Ans.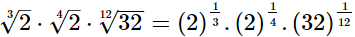
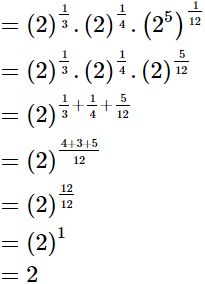
Q.13. Simplify
(i) 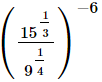
(ii)
(iii)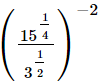
Ans.
(i) 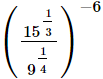
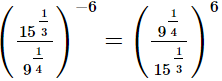
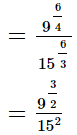
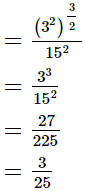
(ii)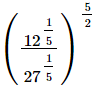
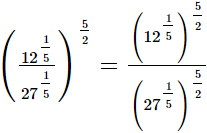
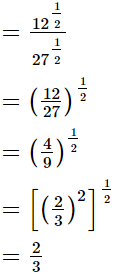
(iii)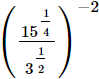
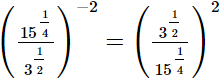
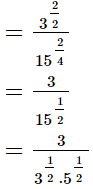
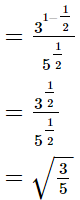
Q.14. Find the value of x in each of the following.
(i)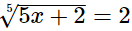
(ii)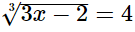
(iii)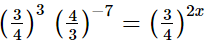
(iv)5x−3 × 32x−8 = 225
(v)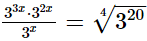
Ans.
(i) 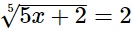
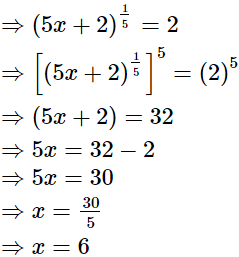
Hence, the value of x is 6.
(ii) 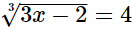
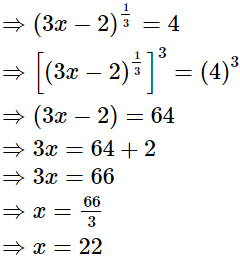
Hence, the value of x is 22.
(iii) 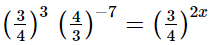

Hence, the value of x is 5.
(iv) 5x−3×32x−8 = 225
⇒5x−3 × 32x−8 = (15)2
⇒5x−3 × 32x − 8 = 52 × 32
⇒x − 3 = 2 and 2x − 8 = 2
⇒x = 2 + 3 and 2x = 2 + 8
⇒x = 5 and 2x = 10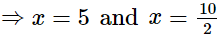
⇒ x = 5 and x = 5
⇒ x = 5
Hence, the value of x is 5.
(v)
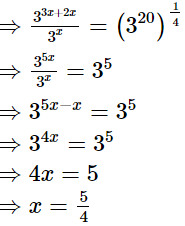
Hence, the value of x is 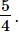
Q.15.
Prove that
(i)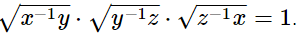
(ii)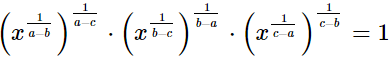
(iii)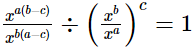
(iv)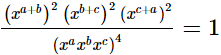
Ans.
(i) 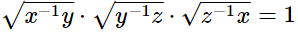
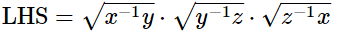
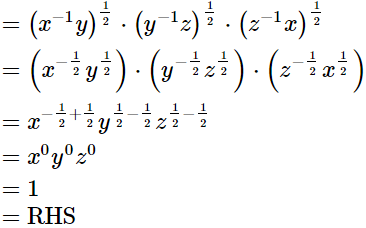
Hence, 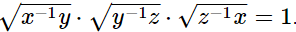
(ii)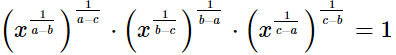
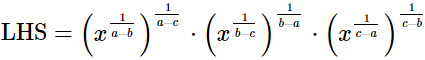
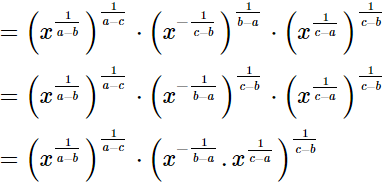
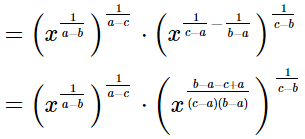
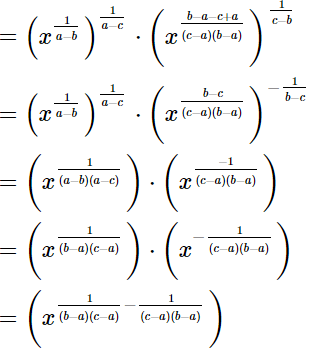
=x0
=1
= RHS
Hence,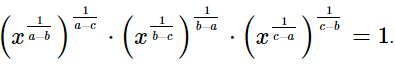
(iii)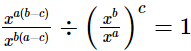
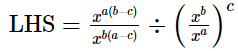
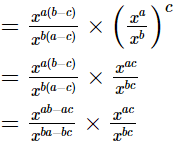
=xab−ac−ba+bc.xac−bc
=x−ac+bc.xac−bc
=x−ac+bc+ac−bc
=x0
= 1
= RHS
Hence, 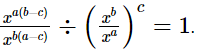
(iv) 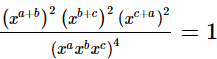
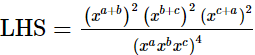
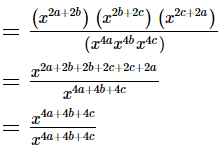
= 1
= RHS
Q.16. If x is a positive real number and exponents are rational numbers, simplify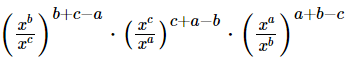
Ans.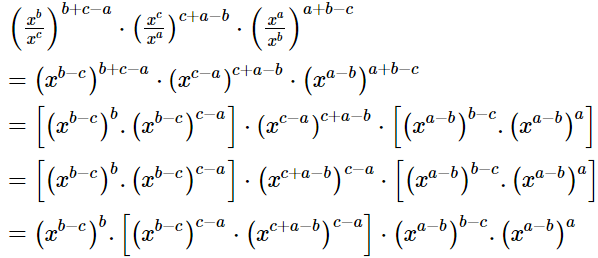
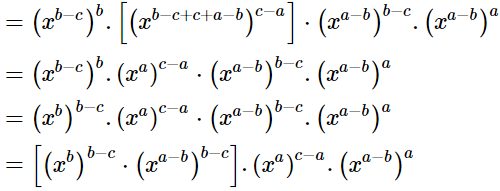
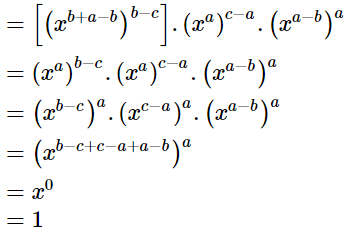
Q.17. If 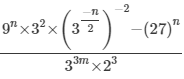 = 1/27, prove that m – n = 1.
= 1/27, prove that m – n = 1.
Ans.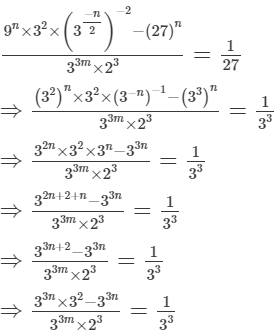
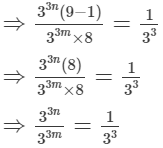
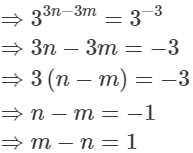
Hence, m - n = 1
Q.18. Write the following in ascending order of magnitude.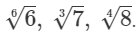
Ans.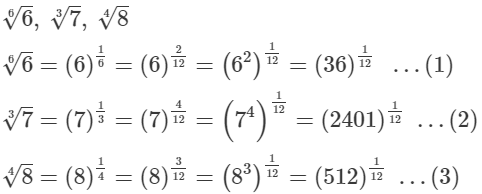
On Comparing (1), (2) and (3), we get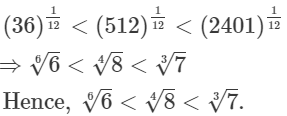
|
1 videos|228 docs|21 tests
|
FAQs on RS Aggarwal Solutions: Exercise 1G - Number System - Extra Documents & Tests for Class 9
| 1. What is the purpose of R.S. Aggarwal Solutions for Class 9 Number System? |  |
| 2. How can R.S. Aggarwal Solutions for Class 9 Number System help in exam preparation? |  |
| 3. Are the solutions in R.S. Aggarwal Solutions for Class 9 Number System easy to understand? |  |
| 4. Can R.S. Aggarwal Solutions for Class 9 Number System be used for self-study? |  |
| 5. Are R.S. Aggarwal Solutions for Class 9 Number System available in the same language as the article title? |  |





















