Operations of Matrix | Mathematics (Maths) for JEE Main & Advanced PDF Download
Elementary Operations
A matrix is an array of numbers arranged in the form of rows and columns. The number of rows and columns of a matrix are known as its dimensions which is given by m x n, where m and n represent the number of rows and columns respectively. Apart from basic mathematical operations there are certain elementary operations that can be performed on matrix namely transformations. It is a special type of matrix that can be illustrate 2d and 3d transformations. Let’s have a look on different types of elementary operations.
Types of Elementary Operations
There are two types of elementary operations of a matrix:
- Elementary row operations: when they are performed on rows of a matrix.
- Elementary column operations: when they are performed on columns of a matrix.
Elementary Operations of a Matrix
- Any 2 columns (or rows) of a matrix can be exchanged. If the ith and jth rows are exchanged, it is shown by Ri ↔ Rj and if the ith and jth columns are exchanged, it is shown by Ci ↔ Cj.
For example, given the matrix A below:
A =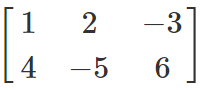
We apply R1 ↔ R2,and obtain:
A =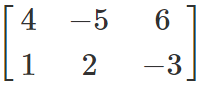
- The elements of any row (or column) of a matrix can be multiplied with a non-zero number. So if we multiply the ith row of a matrix by a non-zero number k, symbolically it can be denoted by Ri ↔ kRi. Similarly, for column it is given by Ci ↔ kCi.
For example, given the matrix A below:
A =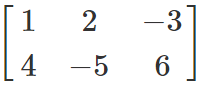
We apply R1 ↔ 3R1and obtain:
A =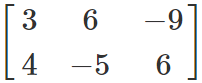
- The elements of any row (or column) can be added with the corresponding elements of another row (or column) which is multiplied by a non-zero number. So if we add the ith row of a matrix to the jth row which is multiplied by a non-zero number k, symbolically it can be denoted by Ri ↔ Ri + kRj. Similarly, for column it is given by Ci ↔ Ci + kCj.
For example, given the matrix A below:
A =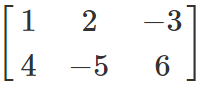
We apply R2 ↔ R2 + 4R1 and obtain:
A =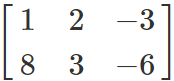
Invertible Matrices
A matrix is an array of numbers arranged in the form of rows and columns. The number of rows and columns of a matrix are known as its dimensions, which is given by m x n where m and n represent the number of rows and columns respectively. The basic mathematical operations like addition, subtraction, multiplication and division can be done on matrices. In this article, we will discuss the inverse of a matrix or the invertible vertices.
What is Invertible Matrix?
A matrix A of dimension n x n is called invertible if and only if there exists another matrix B of the same dimension, such that AB = BA = I, where I is the identity matrix of the same order. Matrix B is known as the inverse of matrix A. Inverse of matrix A is symbolically represented by A-1. Invertible matrix is also known as a non-singular matrix or nondegenerate matrix.
For example, matrices A and B are given below:
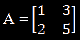
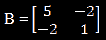
Now we multiply A with B and obtain an identity matrix: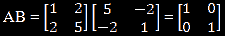
Similarly, on multiplying B with A, we obtain the same identity matrix: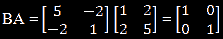
It can be concluded here that AB = BA = I. Hence A-1 = B, and B is known as the inverse of A. Similarly, A can also be called an inverse of B, or B-1 = A.
A square matrix that is not invertible is called singular or degenerate. A square matrix is called singular if and only if the value of its determinant is equal to zero. Singular matrices are unique in the sense that if the entries of a square matrix are randomly selected from any finite region on the number line or complex plane, then the probability that the matrix is singular is 0, that means, it will “rarely” be singular.
Invertible Matrix Theorem
Theorem 1
If there exists an inverse of a square matrix, it is always unique.
Proof:
Let us take A to be a square matrix of order n x n. Let us assume matrices B and C to be inverses of matrix A.
Now AB = BA = I since B is the inverse of matrix A.
Similarly, AC = CA = I.
But, B = BI = B (AC) = (BA) C = IC = C
This proves B = C, or B and C are the same matrices.
Theorem 2:
If A and B are matrices of the same order and are invertible, then (AB)-1 = B-1 A-1.
Proof:
(AB)(AB)-1 = I (From the definition of inverse of a matrix)
A-1 (AB)(AB)-1 = A-1 I (Multiplying A-1 on both sides)
(A-1 A) B (AB)-1 = A-1 (A-1 I = A-1 )
I B (AB)-1 = A-1
B (AB)-1 = A-1
B-1 B (AB)-1 = B-1 A-1
I (AB)-1 = B-1 A-1
(AB)-1 = B-1 A-1
Matrix Inversion Methods
Matrix inversion is the method of finding the other matrix, say B that satisfies the previous equation for the given invertible matrix, say A. Matrix inversion can be found using the following methods:
- Gaussian Elimination
- Newton’s Method
- Cayley-Hamilton Method
- Eigen Decomposition Method
Applications of Invertible Matrix
For many practical applications, the solution for the system of the equation should be unique and it is necessary that the matrix involved should be invertible. Such applications are:
- Least-squares or Regression
- Simulations
- MIMO Wireless Communications
Invertible Matrix Example
Now, go through the solved example given below to understand the matrix which can be invertible and how to verify the relationship between matrix inverse and the identity matrix.
Example: If 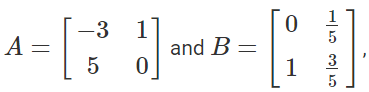 then show that A is invertible matrix and B is its inverse.
then show that A is invertible matrix and B is its inverse.
Solution:
Given,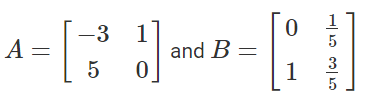
Now, finding the determinant of A,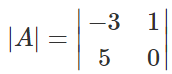
= -3(0) – 1(5)
= 0 – 5
= -5 ≠ 0
Thus, A is an invertible matrix.
We know that, if A is invertible and B is its inverse, then AB = BA = I, where I is an identity matrix.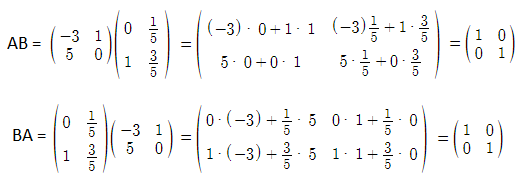
AB = BA = I
Therefore, the matrix A is invertible and the matrix B is its inverse.
Properties
Below are the following properties hold for an invertible matrix A:
- (A−1)−1 = A
- (kA)−1 = k−1A−1 for any nonzero scalar k
- (Ax)+ = x+A−1 if A has orthonormal columns, where + denotes the Moore–Penrose inverse and x is a vector
- (AT)−1 = (A−1)T
- For any invertible n x n matrices A and B, (AB)−1 = B−1A−1. More specifically, if A1, A2…, Ak are invertible n x n matrices, then (A1A2⋅⋅⋅Ak-1Ak)−1 = A−1kA−1k−1⋯A−12A−11
- det A−1 = (det A)−1
Operations on Matrices:

Algebra of matrix involves the operation of matrices, such as Addition, subtraction, multiplication etc.
Let us understand the operation of the matrix in a much better way-
1. Addition of Matrices :
Let A and B be two matrices of same order (i.e. comparable matrices). Then A + B is defined to be
2. Substraction of Matrices :
Let A & B be two matrices of same order. Then A – B is defined as A + (–B) where – B is (–1) B.
3. Multiplication of Matrix By Scalar :
Let λ be a scalar (real or complex number) & A = [aij]m × n be a matrix. Thus the product λA is defined as λA = [bij]m × n where bij = λaij for all i & j.
Note : If A is a scalar matrix, then A = λI, where λ is the diagonal element.
Properties of Addition & Scalar Multiplication :
Consider all matrices of order m × n, whose elements are from a set F (F denote Q, R or C).
Let Mm× n (F) denote the set of all such matrices. Then
4. Multiplication of Matrices :
Let A and B be two matrices such that the number of columns of A is same as number of rows of B. i.e., A = where
which is the dot product of ith row vector of A and jth column vector of B.
Note :
1. The product AB is defined iff the number of columns of A is equal to the number of rows of B. A is called as premultiplier & B is called as post multiplier. AB is defined
BA is defined.
2. In general ABBA, even when both the products are defined.
3. A(BC) = (AB) C, whenever it is defined.
Properties of Matrix Multiplication :
Consider all square matrices of order ‘n’. Let Mn (F) denote the set of all square matrices of order n, (where F is Q, R or C). Then
(a) A, B ∈ Mn (F) ⇒ AB ∈ Mn(F)
(b) In general AB ≠ BA
(c) (AB) C = A(BC)
(d) In, the identity matrix of order n, is the multiplicative identity. AIn = A = InA
(e) For every non singular matrix A(i.e., |A| ≠ 0) of Mn (F) there exist a unique (particular) matrix B ∈ Mn (F) so that AB = In = BA. In this case we say that A & B are multiplicative inverse of one another. In notations, we write B = A-1 or A = B-1.
(f) If λ is a scalar (λA) B = λ(AB) = A(λB).
Note :
1. Let A = [aij]m × n. Then AIn = A & Im A = A, where In & Im are identity matrices of order n & m respectively.
2. For a square matrix A, A2 denotes AA, A3 denotes AAA etc.
Solved Examples:
Ex.1 For the following pairs of matrices, determine the sum and difference, if they exist.
(a)
(b)
Sol. (a) Matrices A and B are 2 × 3 and confirmable for addition and subtraction.
(b) Matrix A is 2 × 2, and B is 2 × 3. Since A and B are not the same size, they are not confirmable for addition or subtraction.
Ex.2 Find the additive inverse of the matrix A =
Sol. The additive inverse of the 3 × 4 matrix A is the 3 × 4 matrix each of whose elements is the negative of the corresponding element of A. Therefore if we denote the additive inverse of A by – A, we have . Obviously A + (–A) = (–A) + A = O, where O is the null matrix of the type 3 × 4.
Ex.3 If find the matrix D such that A + B – D = 0.
Sol. We have A + B – D = 0 ⇒ (A + B) + (-D) = 0 ⇒ A + B = (-D) = D
Ex.4 If verify that 3(A + B) = 3A + 3B.
Sol.
∴ 3 (A + B) = 3A + 3B, i.e. the scalar multiplication of matrices distributes over the addition of matrices.
Ex.5 The set of natural numbers N is partitioned into arrays of rows and columns in the form of matrices as
and so on. Find the sum of the elements of the diagonal in Mn.
Sol. Let Mn = (aij) where i, j = 1, 2, 3,.........,n.
We first find out a11 for the nth matrix; which is the nth term in the series ; 1, 2, 6,......
Let S = 1 + 2 + 6 + 15 +..... + Tn – 1 + Tn.
Again writing S = 1 + 2 + 6 +.... + Tn – 1 + Tn
⇒ 0 = 1 + 1 + 4 + 9 +..... + (Tn – Tn – 1) – Tn ⇒ Tn = 1 + (1 + 4 + 9 +....... upto (n – 1) terms)
= 1 + (1 2 + 22 + 32 + 42 +..... + (n – 1)2)
Ex.6
Sol.
The matrix AB is of the type 3 × 3 and the matrix BA is also of the type 3 × 3. But the corresponding elements of these matrices are not equal. Hence AB≠ BA.
Ex.7 Show that for all values of p, q, r, s the matrices,
Sol.
for all values of p, q, r,s. Hence PQ = QP, for all values of p, q, r, s.
Ex.8 where k is any positive integer.
Sol. We shall prove the result by induction on k.
We shall prove the result by induction on k.
We have Thus the result is true when k = 1.
Now suppose that the result is true for any positive integer k.
where k is any positive integer.
Now we shall show that the result is true for k + 1 if it is true for k. We have
Thus the result is true for k + 1 if it is true for k. But it is true for k = 1. Hence by induction it is true for all positive integral value of k.
Ex.9 where I is the two rowed unit matrix n is a positive integer.
Sol.
= 0 ⇒ A3 = A2 . A = 0 ⇒ A2 = A3 = A4 =...... An = 0
Now by binomial theorem
(a I + b A)n = (a I)n + nC1(a I)n – 1 b A + nC2 (a I)n – 2 (b A)2 +..... + nCn (b A)n
= an I + nC1 an – 1 b I A + nC2 an – 2 b2 I A2 +...... + nCn bn An
= an I + n an – 1 b A + 0......
Ex.10 If then find the value of (n + a).
Sol. Consider
Hence n = 9 and 2007 =
⇒ 2007 = 9a + 32 · 9 = 9(a + 32)
⇒ a + 32 = 223 ⇒ a = 191
hence a + n = 200
Ex.11 Find the matrices of transformations T1T2 and T2T1, when T1 is rotation through an angle 60º and T2 is the reflection in the y–axis. Also verify that T1T2 T2T1.
Sol.
...(1)
It is clear from (1) and (2), T1T2 ≠ T2T1
Ex.12 Find the possible square roots of the two rowed unit matrix I.
Sol.
be square root of the matrix =
Since the above matrices are equal, therefore
a2 + bc =1 ...(i)
ab + bd = 0 ...(ii)
ac + cd = 0 ,,,(iii)
cb + d2 = 0 ....(iv)
must hold simultaneously.
If a + d = 0, the above four equations hold simultaneously if d = –a and a2 + bc =1
Hence one possible square root of I is
where α, β, γ are any three numbers related by the condition α2 + βγ = 1.
If a + d ≠ 0, the above four equations hold simultaneously if b = 0, c = 0, a = 1, d = 1 or if b = 0, c = 0, a = –1, d = –1. Hence i.e. ± I are other possible square roots of I.
Ex.13 then prove that
Sol.
...(i)
...(ii)
...(iii)
Similarly it can be shown that A4 = 23 x4 E, A5 = 24 x5 E ...
D. FURTHER TYPES OF MATRICES
(a) Nilpotent matrix : A square matrix A is said to be nilpotent (of order 2) if, A2 = O.
A square matrix is said to be nilpotent of order p, if p is the least positive integer such that Ap = O
(b) Idempotent matrix : A square matrix A is said to be idempotent if, A2 = A. eg. is an idempotent matrix.
(c) Involutory matrix : A square matrix A is said to be involutory if A2 = I,I being the identity matrix. eg. A = is an involutory matrix.
(d) Orthogonal matrix : A square matrix A is said to be an orthogonal matrix if A'A = I = A'A
(e) Unitary matrix : A square matrix A is said to be unitary if is the complex conjugate of A.
Ex.14 Find the number of idempotent diagonal matrices of order n.
Sol. Let A = diag (d1, d2,....., dn) be any diagonal matrix of order n.
now A2 = A . A =
But A is idempotent, so A2 = A and hence corresponding elements of A2 and A should be equal
∴ or d1 = 0, 1; d2 = 0, 1;.........;dn = 0, 1
⇒ each of d1, d2 ......, dn can be filled by 0 or 1 in two ways.
⇒ Total number of ways of selecting d1, d2,......., dn = 2n
Hence total number of such matrices = 2n.
Ex.15 Show that the matrix A = is nilpotent and find its index.
Sol.
Thus 3 is the least positive integer such that A3 = 0. Hence the matrix A is nilpotent of index 3.
Ex.16 If AB = A and BA = B then B'A' = A' and A'B' = B' and hence prove that A' and B' are idempotent.
Sol. We have AB = A ⇒ (AB)' = A' ⇒ B'A' = A'. Also BA = B ⇒ (BA)' = B' ⇒ A'B' = B'.
Now A' is idempotent if A'2 = A'. We have A'2 =A'A' = A' (B'A') = (A'B') A' = B'A' =A'.
∴ A' is idempotent.
Again B'2 = B'B' = B' (A'B') = (B'A') B' = A'B' = B'. ∴ B' is idempotent.
E. TRANSPOSE OF MATRIX
Let A = [aij]m × n. Then the transpose of A is denoted by A'(or AT) and is defined as A' = [bij]n × m where bij = aji for all i & j
i.e. A' is obtained by rewriting all the rows of A as columns (or by rewriting all the columns of A as rows).
(i) For any matrix A = [aij]m × n, (A')' = A
(ii) Let λ be a scalar & A be a matrix. Then (λA)' = λA'
(iii) (A + B)' = A' + B' & (A - B)' = A' - B' for two comparable matrices A and B.
(iv) (A1 ± A2 ±.... ± An)' = A1' ± A2' ±..... ± An', where Aj are comparable.
(v) Let A = [aij]m × p & B = [bij]p × n, then (AB)' = B'A'
(vi) (A1 A2 ......... An)' = An'. An-1'..................± A2'. A1', provided the product is defined.
(vii) Symmetric & Skew–Symmetric Matrix : A square matrix A is said to be symmetric if A' = A
i.e. Let A = [aij]n. A is symmetric iff aij = aij for all i & j.
A square matrix A is said to be skew–symmetric if A' = - A
i.e. Let A = [aij]n. A is skew–symmetric iff aij = –aji for all i & j.
is a symmetric matrix
is a skew–symmetric matrix.
Note :
1. In skew–symmetric matrix all the diagonal elements are zero. (aij = - aij ⇒ aij = 0)
2. For any square matrix A, A + A' is symmetric & A -A' is skew - symmetric.
3. Every square matrix can be uniquely expressed as a sum of two square matrices of which one is symmetric and the other is skew–symmetric.
|
172 videos|503 docs|154 tests
|
FAQs on Operations of Matrix - Mathematics (Maths) for JEE Main & Advanced
| 1. What are elementary operations on matrices? |  |
| 2. How can elementary operations be used to find the inverse of a matrix? |  |
| 3. What is the significance of invertible matrices in linear algebra? |  |
| 4. Can all matrices be inverted? |  |
| 5. How do operations on matrices help in solving systems of equations? |  |
















