Transpose and Inverse of a Matrix | Mathematics (Maths) for JEE Main & Advanced PDF Download
What is a matrix?
A matrix is a rectangular array of numbers or functions arranged in a fixed number of rows and columns. There are many types of matrices. Let us consider a matrix to understand more about them.
A =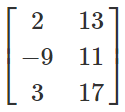
3x2 order matrix
The above matrix A is of order 3 × 2. Thus, there are a total of 6 elements.
The horizontal array is known as rows and the vertical array are known as Columns.
Now, let us take another matrix.
B =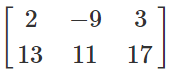
2x3 order matrix
The number of rows in matrix A is greater than the number of columns, such a matrix is called a Vertical matrix.
The number of columns in matrix B is greater than the number of rows. Such a matrix is called a Horizontal matrix.
One thing to notice here, if elements of A and B are listed, they are the same in number and each element which is there in A is there in B too. So, is A = B?
Before answering this, we should know how to decide the equality of the matrices.
A matrix P is said to be equal to matrix Q if their orders are the same and each corresponding element of P is equal to that of Q.
That is, if P =[pij]mxn and Q = [qij]rxs are two matrices such that P = Q, then:
- m = r and n = s i.e. the orders of the two matrices must be same
- For every value of i and j, pij = qij.
How to Find Transpose of a Matrix?
Let us now go back to our original matrices A and B. Though they have the same set of elements, are they equal?
The answer is no. That’s because their order is not the same. Now, there is an important observation. There can be many matrices which have exactly the same elements as A has.
Here, the number of rows and columns in A is equal to number of columns and rows in B respectively. Thus, the matrix B is known as the Transpose of the matrix A. The transpose of matrix A is represented by A' or AT. The following statement generalizes transpose of a matrix:
If A = [aij]m×n, then A' = [aij]n×m.
Thus Transpose of a Matrix is defined as “A Matrix which is formed by turning all the rows of a given matrix into columns and vice-versa.”
Let’s Work Out-
Example- Find the transpose of the given matrix
M =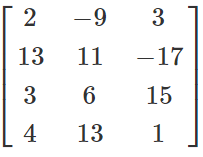
Solution- Given a matrix of the order 4×3.
Transpose of a matrix is given by interchanging of rows and columns.
MT =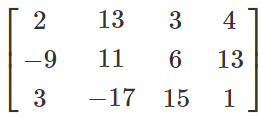
Properties of Transpose of a Matrix
To understand the properties of transpose matrix, we will take two matrices A and B which have equal order. Some properties of transpose of a matrix are given below:
(i) Transpose of the Transpose Matrix
If we take transpose of transpose matrix, the matrix obtained is equal to the original matrix. Hence, for a matrix A, (A’ )' = A
What basically happens, is that any element of A, i.e. aij gets converted to aji if transpose of A is taken. So, taking transpose again, it gets converted to aij, which was the original matrix A.
Example: If N =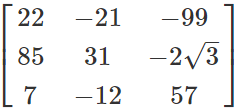
,
Then N’ =
Now, (N’)'=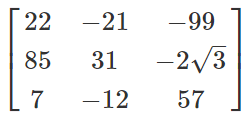
= N
(ii) Addition Property of Transpose
Transpose of an addition of two matrices A and B obtained will be exactly equal to the sum of transpose of individual matrix A and B.
This means,
(A+B)' = A’+B'
Example- If P = 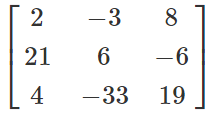
and Q = 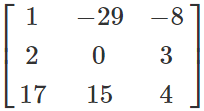
P + Q =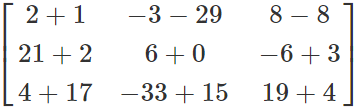
= 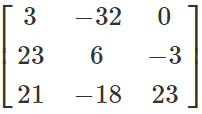
(P+Q)' =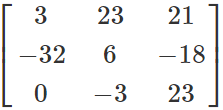
P’+Q'=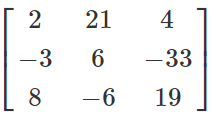
+ 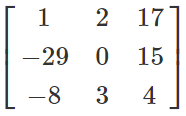
= 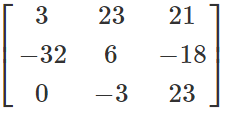
= (P+Q)'
So, we can observe that (P+Q)' = P’+Q'.
(iii) Multiplication by Constant
If a matrix is multiplied by a constant and its transpose is taken, then the matrix obtained is equal to transpose of original matrix multiplied by that constant. That is,
(kA)' = kA', where k is a constant
Example- If P =
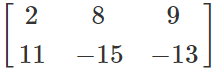
2x3 order matrix and k is a constant, then (kP)'=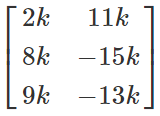
2x3 order matrix
kP'= k
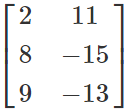
2x3 order matrix = 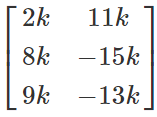
2x3 = (kP)'
We can observe that (kP)' = kP'.
(iv) Multiplication Property of Transpose
Transpose of the product of two matrices is equal to the product of transpose of the two matrices in reverse order. That is
(AB)' = B’A'
Example: A = 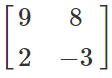
and B =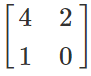
Let us find A×B.
A×B =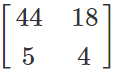
→ (AB)’ =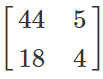
B’A' =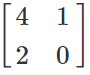
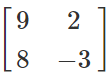
=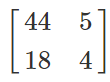
= (AB)'
∴ (AB)' = B’A'
A’B' =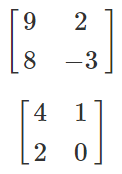
=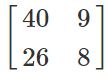
We can clearly observe from here that (AB)’≠A’B’.
Those were properties of matrix transpose which are used to prove several theorems related to matrices.
The adjoint of a matrix (also called the adjugate of a matrix) is defined as the transpose of the cofactor matrix of that particular matrix. For a matrix A, the adjoint is denoted as adj (A). On the other hand, the inverse of a matrix A is that matrix which when multiplied by the matrix A give an identity matrix. The inverse of a Matrix A is denoted by A-1.
Adjoint of a Matrix
Let the determinant of a square matrix A be |A|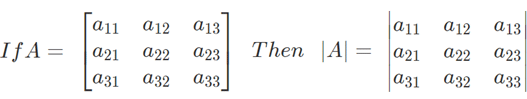
The matrix formed by the cofactors of the elements is
Where 
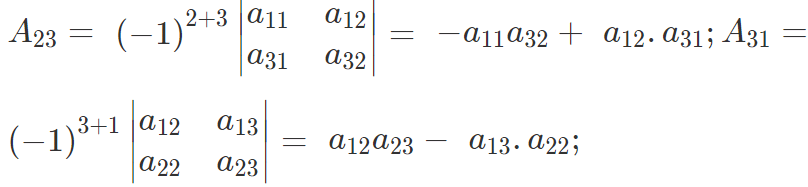
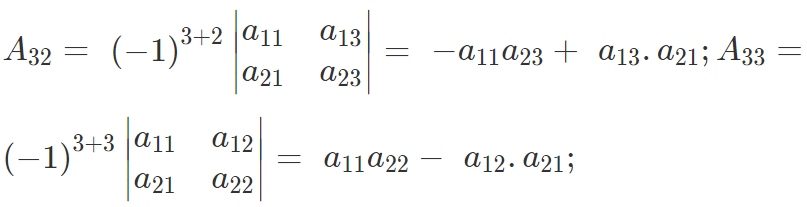
Then the transpose of the matrix of co-factors is called the adjoint of the matrix A and is written as adj A.
The product of a matrix A and its adjoint is equal to unit matrix multiplied by the determinant A.
Let A be a square matrix, then (Adjoint A). A = A. (Adjoint A) = | A |. I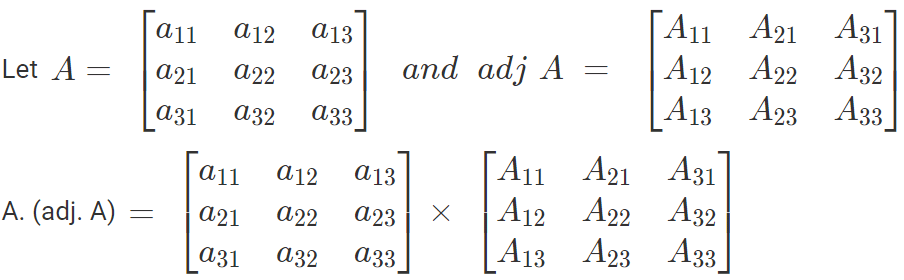
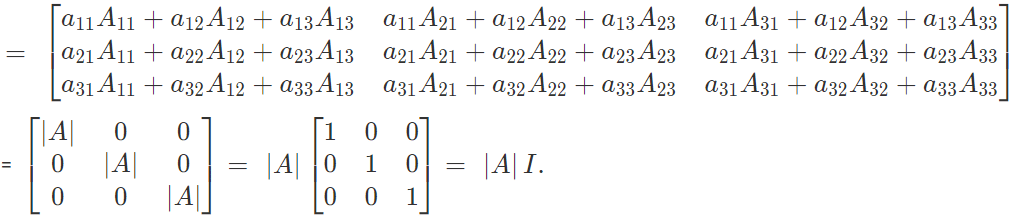
Example Problems on How to Find the Adjoint of a Matrix
Example 1: If AT = – A then the elements on the diagonal of the matrix are equal to
(a) 1
(b) -1
(c) 0
(d) none of these
Solution: (c) AT = -A; A is skew-symmetric matrix; diagonal elements of A are zeros.
so option (c) is the answer.
Example 2: If A and B are two skew-symmetric matrices of order n, then,
(a) AB is a skew-symmetric matrix
(b) AB is a symmetric matrix
(c) AB is a symmetric matrix if A and B commute
(d) None of these
Solution: (c) We are given A’ = -A and B’ = -B;
Now, (AB)’ = B’A’ = (-B) (-A) = BA = AB, if A and B commute.
Example 3: Let A and B be two matrices such that AB’ + BA’ = 0. If A is skew symmetric, then BA
(a) Symmetric
(b) Skew symmetric
(c) Invertible
(d) None of these
Solution: (c) we have, (BA)’ = A’B’ = -AB’ [ A is skew symmetric]; = BA’ = B(-A) = -BA
BA is skew symmetric.
Example 4: Let A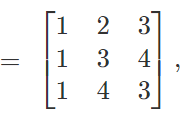
then adj A is given by –
Solution: Co-factors of the elements of any matrix are obtained by eliminating all the elements of the same row and column and calculating the determinant of the remaining elements.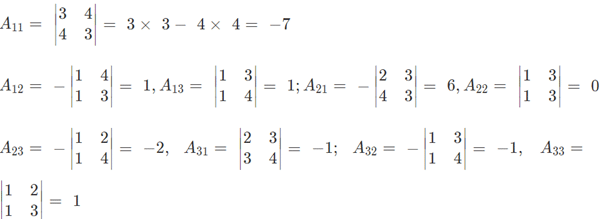
adj A = transpose of cofactor matrix.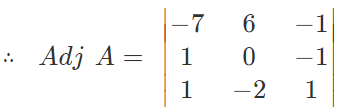
Example 5: Which of the following statements are false –
(a) If | A | = 0, then | adj A | = 0;
(b) Adjoint of a diagonal matrix of order 3 × 3 is a diagonal matrix;
(c) Product of two upper triangular matrices is an upper triangular matrix;
(d) adj (AB) = adj (A) adj (B);
Solution: (d) We have, adj (AB) = adj (B) adj (A) and not adj (AB) = adj (A) adj (B)
Inverse of a Matrix
If A and B are two square matrices of the same order, such that AB = BA = I (I = unit matrix)
Then B is called the inverse of A, i.e. B = A–1 and A is the inverse of B. Condition for a square matrix A to possess an inverse is that the matrix A is non-singular, i.e., | A | ≠ 0. If A is a square matrix and B is its inverse then AB = I. Taking determinant of both sides | AB | = | I | or | A | | B | = I. From this relation it is clear that | A | ≠ 0, i.e. the matrix A is non-singular.
How to find the inverse of a matrix by using the adjoint matrix?
We know that,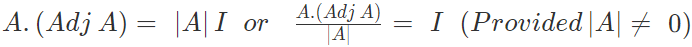
And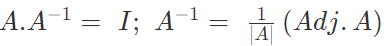
Properties of Inverse and Adjoint of a Matrix
- Property 1: For a square matrix A of order n, A adj(A) = adj(A) A = |A|I, where I is the identitiy matrix of order n.
- Property 2: A square matrix A is invertible if and only if A is a non-singular matrix.
Problems on Finding the Inverse of a Matrix
Illustration : Let A 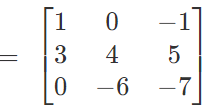
What is inverse of A?
Solution: By using the formula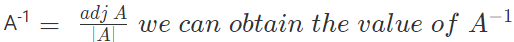
We have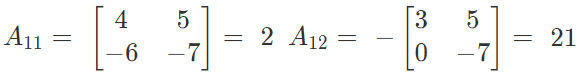
Similarly
A13 = -18 A31 =4, A32 = −8, A33 = 4, A21 = +6, A22 = −7, A23 = 6
cofactor matrix of A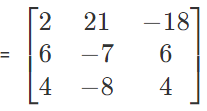
adj A = transpose of cofactor matrix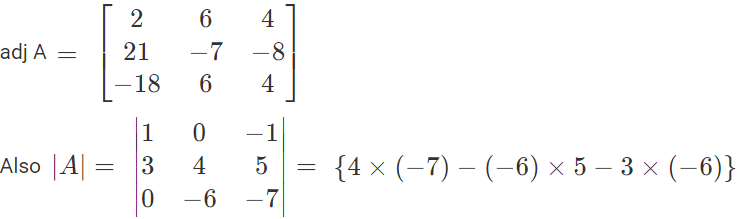
= -28 + 30 + 18
= 20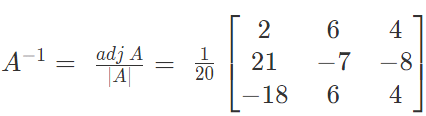
|
172 videos|476 docs|154 tests
|
FAQs on Transpose and Inverse of a Matrix - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the adjoint of a matrix? |  |
| 2. How is the inverse of a matrix calculated? |  |
| 3. What is the relationship between the transpose and inverse of a matrix? |  |
| 4. How are the transpose and inverse of a matrix used in practical applications? |  |
| 5. Can any matrix have an inverse? |  |
















