Properties of Inverse Trigonometric Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download

There are a few inverse trigonometric functions properties which are crucial to not only solve problems but also to have a deeper understanding of this concept. To recall, inverse trigonometric functions are also called “Arc Functions”. For a given value of a trigonometric function; they produce the length of arc needed to obtain that particular value. The range of an inverse function is defined as the range of values of the inverse function that can attain with the defined domain of the function. The domain of a function is defined as the set of every possible independent variable where the function exists. Inverse Trigonometric Functions are defined in a certain interval.

Considering the domain and range of the inverse functions, following formulas are important to be noted:

• sin(sin⁻¹x) = x, if -1 ≤ x ≤ 1
• cos(cos⁻¹x) = x, if -1 ≤ x ≤ 1
• tan(tan⁻¹x) = x, if -∞ ≤ x ≤∞
• cot(cot⁻¹x) = x, if -∞≤ x ≤∞
• sec(sec⁻¹x) = x, if -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞
• cosec(cosec⁻¹x) = x, if -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞

Also, the following formulas are defined for inverse trigonometric functions.

• sin⁻¹(sin y) = y, if -π/2 ≤ y ≤ π/2
• cos⁻¹(cos y) =y, if 0 ≤ y ≤ π
• tan⁻¹(tan y) = y, if -π/2 <y< π/2
• cot⁻¹(cot y) = y if 0<y< π
• sec⁻¹(sec y) = y, if 0 ≤ y ≤ π, y ≠ π/2
• cosec⁻¹(cosec y) = y if -π/2 ≤ y ≤ π/2, y ≠ 0

Important Properties of Inverse Trigonometric Functions

Here are a few important properties related to inverse trigonometric functions:

Property Set 1

• Sin⁻¹(x) = cosec⁻¹(1/x), x∈ [−1,1]−{0}
• Cos⁻¹(x) = sec⁻¹(1/x), x ∈ [−1,1]−{0}
• Tan⁻¹(x) = cot⁻¹(1/x), if x > 0  (or)  cot⁻¹(1/x) −π, if x < 0
• Cot⁻¹(x) = tan⁻¹(1/x), if x > 0 (or) tan⁻¹(1/x) + π, if x < 0

Property Set 2

• Sin⁻¹(−x) = −Sin⁻¹(x)
• Tan⁻¹(−x) = −Tan⁻¹(x)
• Cos⁻¹(−x) = π − Cos⁻¹(x)
• Cosec⁻¹(−x) = − Cosec⁻¹(x)
• Sec⁻¹(−x) = π − Sec⁻¹(x)
• Cot⁻¹(−x) = π − Cot⁻¹(x)

Proofs:
1. Sin⁻¹(−x) = −Sin⁻¹(x)
Let sin⁻¹(−x) = y, i.e.,−x = sin y
⇒ x = − sin y
Thus,
x = sin (− y)
Or,
sin⁻¹(x) = −y = −sin⁻¹(−x)
Therefore, sin⁻¹(−x) = −sin⁻¹(x)
Similarly, using the same concept following results can be obtained:

• cosec⁻¹(−x) = −cosec⁻¹x, |x|≥1
• tan⁻¹(−x) = −tan⁻¹x, xϵR

2. Cos⁻¹(−x) = π − Cos⁻¹(x) 
Let cos⁻¹(−x) = y i.e., −x = cos y
⇒ x = −cos y = cos(π–y)
Thus,
cos⁻¹(x) = π–y
Or,
cos⁻¹(x) = π–cos⁻¹(−x)
Therefore, cos⁻¹(−x) = π–cos⁻¹(x)
Similarly using the same concept following results can be obtained:

• sec⁻¹(−x) = π–sec⁻¹x, |x|≥1
• cot⁻¹(−x) = π–cot⁻¹x, xϵR

Property Set 3

• Sin⁻¹(1/x) = cosec⁻¹x, x≥1 or x≤−1
• Cos⁻¹(1/x) = sec⁻¹x, x≥1 or x≤−1
• Tan⁻¹(1/x) = −π + cot⁻¹(x)

Proof: Sin⁻¹(1/x) = cosec⁻¹x, x≥1 or x≤−1
Let cosec⁻¹ x = y, i.e. x = cosec y
⇒ (1/x) = sin y
Thus, sin⁻¹(1/x) = y
Or,
sin⁻¹(1/x) = cosec⁻¹x
Similarly using the same concept the other results can be obtained.
Illustrations: 

• sin⁻¹(⅓) = cosec⁻¹(3)
• cos⁻¹(¼) = sec⁻¹(4)
• sin⁻¹(−¾) = cosec⁻¹(−4/3) = sin⁻¹(3/4)
• tan⁻¹(−3) = cot⁻¹(−⅓)−π

Property Set 4

• Sin⁻¹(cos θ) = π/2 − θ, if θ∈[0,π]
• Cos⁻¹(sin θ) = π/2 − θ, if θ∈[−π/2, π/2]
• Tan⁻¹(cot θ) = π/2 − θ, θ∈[0,π]
• Cot⁻¹(tan θ) = π/2 − θ, θ∈[−π/2, π/2]
• Sec⁻¹(cosec θ) = π/2 − θ, θ∈[−π/2, 0]∪[0, π/2]
• Cosec⁻¹(sec θ) = π/2 − θ, θ∈[0,π]−{π/2}
• Sin⁻¹(x) = cos⁻¹[√(1−x²)], 0≤x≤1

= −cos⁻¹[√(1−x²)], −1≤x<0

Illustrations:
1. Given, cos⁻¹(−3/4) = π − sin⁻¹A. Find A.  
Solution: Draw the diagram from the question statement.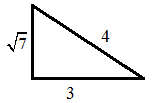

So,
cos⁻¹(−3/4) = π − sin⁻¹(√7/4)
Thus, A = √7/4
2. cos⁻¹(¼) = sin⁻¹ √(1−1/16) = sin⁻¹(√15/4)
3. sin⁻¹(−½) = −cos⁻¹√(1−¼) = −cos⁻¹(√3/2)
4. sin²(tan⁻¹(¾)) = sin²(sin⁻¹(⅗)) = (⅗)² = 9/25.
5. sin⁻¹(sin 2π/3) = π/3
6. cos⁻¹(cos 4π/3) = 2π/3
7. sin⁻¹(cos 33π/10) = sin⁻¹cos(3π + 3π/10) = sin⁻¹(−sin(π/2 − 3π/10)) = −(π/2 − 3π/10) = −π/5

Property Set 5

• Sin⁻¹x + Cos⁻¹x = π/2
• Tan⁻¹x + Cot⁻¹(x) = π/2
• Sec⁻¹x + Cosec⁻¹x = π/2

Proof: sin⁻¹(x) + cos⁻¹(x) = (π/2), xϵ[−1,1]
Let sin⁻¹(x) = y, i.e., x = sin y = cos((π/2) − y)
⇒ cos⁻¹(x) = (π/2) – y = (π/2) − sin⁻¹(x)
Thus,
sin⁻¹(x) + cos⁻¹(x) = (π/2)
Similarly using the same concept following results can be obtained:

• tan⁻¹(x) + cot⁻¹(x) = (π/2), xϵR
• cosec⁻¹(x) + sec⁻¹(x) = (π/2), |x|≥1

Illustrations:
1. Sec⁻¹(4) + Cosec⁻¹(4) = π/2
2. Tan⁻¹(3) + Cot⁻¹(3) = π/2

Property Set 6
(1) If x, y > 0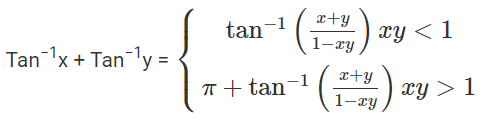

(2) If x, y < 0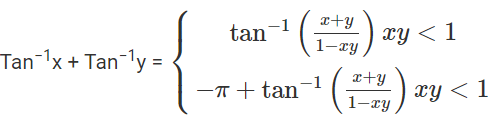


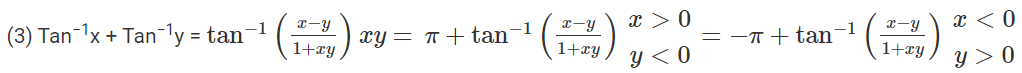
(4) tan⁻¹(x) – tan⁻¹(y) = tan⁻¹[(x−y)/ (1+xy)], xy>−1 
(5) 2tan⁻¹(x) = tan⁻¹[(2x)/ (1–x²)], |x|<1 

Proof: Tan⁻¹(x) + tan⁻¹(y) = tan⁻¹[(x+y)/ (1−xy)], xy<1
Let tan⁻¹(x) = α and tan⁻¹(y) = β, i.e., x = tan(α) and y = tan(β)  
⇒ tan(α+β) = (tan α + tan β) / (1 – tan α tan β) 
Thus,
(α) + (β) = tan⁻¹[(x+y) / (1−xy)]
Therefore,
tan⁻¹(x) + tan⁻¹(y) = tan⁻¹[(x+y) / (1−xy)]

Similarly using the same concept following results can be obtained:

• tan⁻¹(x) – tan⁻¹(y) = tan⁻¹[(x−y)/ (1+xy)], xy>−1
• 2tan⁻¹(x) = tan⁻¹[(2x)/ (1–x²)], |x|<1

Illustrations:
1. Tan⁻¹(−½) + Tan⁻¹(−⅓) = Tan⁻¹[(−½ − ⅓)/ (1− ⅙)]
= tan⁻¹(−1)
= −π/4

2. Tan⁻¹(−2) + Tan⁻¹(−3) = Tan⁻¹[(−2+−3)/ (1−6)]
= Tan⁻¹(−5/ −5) = Tan⁻¹1
= π/4

3. Tan⁻¹(−3) + Tan⁻¹(−⅓) = − (Tan⁻¹B) + Tan⁻¹(⅓)
= −π/2

4. Tan⁻¹(5/3) − Tan⁻¹(¼) = Tan⁻¹[(5/3−¼)/ (1+5/12)]
= Tan⁻¹(17/17)
= Tan⁻¹1 = π/4

5. Tan⁻¹2x + Tan⁻¹3x = π/4
⇒ Tan⁻¹[(5x)/ (1−6x²)] = π/4
⇒ 5x/ (1−6x²) = 1
⇒ 6x² − 5x + 1 = 0
⇒ x = 1/6 or −1
∴ x = 16 as, x = −1

6. If tan⁻¹(4) + Tan⁻¹(5) = Cot⁻¹(λ). Find λ
Here,
Tan⁻¹[9/ (1−20)] = Cot⁻¹λ
⇒ Tan⁻¹(-9/19) = Cot⁻¹(λ)
⇒ −Tan⁻¹(9/19) = Cot⁻¹(λ)
⇒ −Cot⁻¹(19/9) = Cot⁻¹(λ)
Or, λ = −19/9

Property Set 7

• sin⁻¹(x) + sin⁻¹(y) = sin⁻¹[x√(1−y²)+ y√(1−x²)]
• cos⁻¹x + cos⁻¹y = cos⁻¹[xy−√(1−x²)√(1−y²)]

Illustration:
1. sin⁻¹(⅘) + sin⁻¹(7/25) = sin⁻¹(A). Find A.
Solution:
= sin⁻¹(⅘ √{1−(7/25)²} + √{1−(⅘)²} 7/25)
= sin⁻¹(117/125)

2. Prove that sin⁻¹(⅘) + sin(5/13) + sin⁻¹(16/65) = π/2
Solution:
sin⁻¹(63/65) + sin⁻¹(16/65)
= cos⁻¹(16/65) + sin⁻¹(16/65)
= π/2

Property Set 8: Corresponding Graphs

• sin⁻¹(sin x) = −π−π, if x∈[−3π/2, −π/2]

= x, if x∈[−π/2, π/2]
= π−x, if x∈[π/2, 3π/2] 
=−2π+x, if x∈[3π/2, 5π/2] And so on.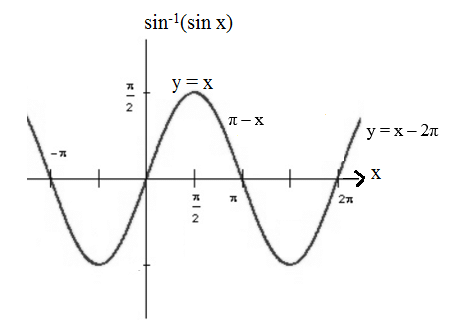

• cos⁻¹(cos x) = 2π+x, if x∈[−2π,−π]

= −x, ∈[−π, 0]
= x, ∈[0, π]
= 2π−x, ∈[π, 2π]
=−2π+x, ∈[2π, 3π]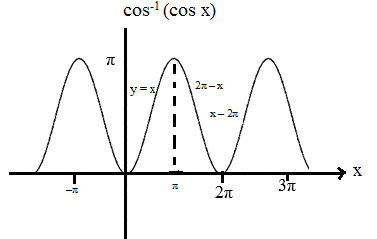

• tan⁻¹(tan x) = π+x, x∈(−3π/2, −π/2)

= x, (−π/2, π/2) 
= x−π, (π/2, 3π/2) 
= x−2π, (3π/2, 5π/2)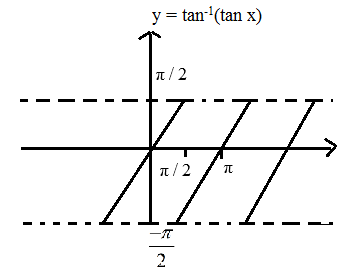

Illustration:
1. sin⁻¹(sin 2π/3) = π−2π/3 = π/3
2. cos⁻¹(cos(13π/6)) = π/6
3. sin⁻¹sin(4) = π−4
4. sin⁻¹sin(6) = 6−2π
5. sin⁻¹sin(12) = 12−4π
6. cos⁻¹(cos 3) = 3
7. cos⁻¹(cos 5) = 2π−5
8. cos⁻¹(cos 6) = 2π−6
9. tan⁻¹(tan 3) = 3−π

Property Set 9

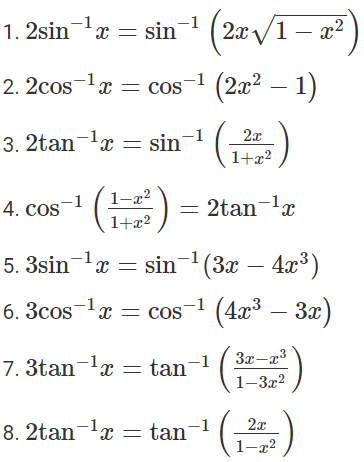
Illustrations:

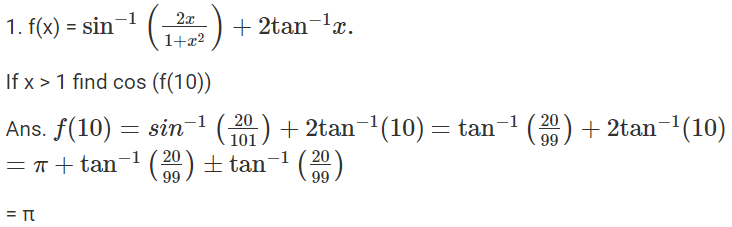
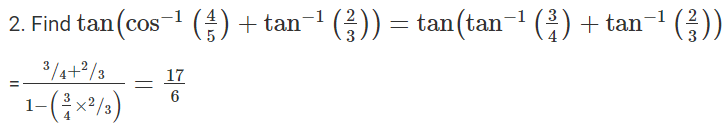
Proof: 2tan⁻¹x = sin⁻¹[(2x)/ (1+x²)], |x|<1
Let, tan⁻¹x = y i.e., x = tan y
⇒ sin⁻¹[(2x)/ (1+x²)] = sin⁻¹[(2tany)/ (1+tan²y)]
Thus,
⇒sin⁻¹[(2tany)/ (1+tan²y)] = sin⁻¹(sin2y) = 2y = 2tan⁻¹x
Similarly using the same concept following results can be concluded:

• 2tan⁻¹x = cos⁻¹[(1–x²)/ (1+x²), x≥0
• 2tan⁻¹x = tan⁻¹[(2x)/ (1–x²), −1<x<1