Sorting Algorithms- 2 - Algorithms - Computer Science Engineering (CSE)

Bubble Sort

Bubble Sort is the simplest comparison-based sorting algorithm. It repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are required, which means the list is sorted.

Example: step-by-step passes

Consider the array: (5 1 4 2 8)

First Pass:

( 5 1 4 2 8 ) → ( 1 5 4 2 8 ). The algorithm compares the first two elements and swaps since 5 > 1.

( 1 5 4 2 8 ) → ( 1 4 5 2 8 ). Swap since 5 > 4.

( 1 4 5 2 8 ) → ( 1 4 2 5 8 ). Swap since 5 > 2.

( 1 4 2 5 8 ) → ( 1 4 2 5 8 ). No swap since 5 < 8.

Second Pass:

( 1 4 2 5 8 ) → ( 1 4 2 5 8 ). No swap needed.

( 1 4 2 5 8 ) → ( 1 2 4 5 8 ). Swap since 4 > 2.

( 1 2 4 5 8 ) → ( 1 2 4 5 8 ). No swap needed.

( 1 2 4 5 8 ) → ( 1 2 4 5 8 ). No swap needed.

After the second pass the array is already sorted, but a complete bubble-sort implementation typically needs one whole pass without any swap to confirm the array is sorted.

Third Pass:

( 1 2 4 5 8 ) → ( 1 2 4 5 8 ) - no swaps during this pass, so algorithm can stop.

Implementations

• C++

  // C++ program for implementation of Bubble sort #include <bits/stdc++.h> using namespace std; void swap(int *xp, int *yp) { int temp = *xp; *xp = *yp; *yp = temp; } // A function to implement bubble sort void bubbleSort(int arr[], int n) { int i, j; for (i = 0; i < n-1; i++) // Last i elements are already in place for (j = 0; j < n-i-1; j++) if (arr[j] > arr[j+1]) swap(&arr[j], &arr[j+1]); } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Driver code int main() { int arr[] = {64, 34, 25, 12, 22, 11, 90}; int n = sizeof(arr)/sizeof(arr[0]); bubbleSort(arr, n); cout<<"Sorted array:
"; printArray(arr, n); return 0; } // This code is contributed by rathbhupendra

• C

  // C program for implementation of Bubble sort #include <stdio.h> void swap(int *xp, int *yp) { int temp = *xp; *xp = *yp; *yp = temp; } // A function to implement bubble sort void bubbleSort(int arr[], int n) { int i, j; for (i = 0; i < n-1; i++) // Last i elements are already in place for (j = 0; j < n-i-1; j++) if (arr[j] > arr[j+1]) swap(&arr[j], &arr[j+1]); } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i=0; i < size; i++) printf("%d ", arr[i]); printf("
"); } // Driver program to test above functions int main() { int arr[] = {64, 34, 25, 12, 22, 11, 90}; int n = sizeof(arr)/sizeof(arr[0]); bubbleSort(arr, n); printf("Sorted array:
"); printArray(arr, n); return 0; }

• Java

  // Java program for implementation of Bubble Sort class BubbleSort { void bubbleSort(int arr[]) { int n = arr.length; for (int i = 0; i < n-1; i++) for (int j = 0; j < n-i-1; j++) if (arr[j] > arr[j+1]) { // swap arr[j+1] and arr[j] int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } /* Prints the array */ void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i] + " "); System.out.println(); } // Driver method to test above public static void main(String args[]) { BubbleSort ob = new BubbleSort(); int arr[] = {64, 34, 25, 12, 22, 11, 90}; ob.bubbleSort(arr); System.out.println("Sorted array"); ob.printArray(arr); } } /* This code is contributed by Rajat Mishra */

• Python

  # Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j] > arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Driver code to test above arr = [64, 34, 25, 12, 22, 11, 90] bubbleSort(arr) print ("Sorted array is:") for i in range(len(arr)): print ("%d" %arr[i], end=" ")

• C#

  // C# program for implementation // of Bubble Sort using System; class GFG { static void bubbleSort(int []arr) { int n = arr.Length; for (int i = 0; i < n - 1; i++) for (int j = 0; j < n - i - 1; j++) if (arr[j] > arr[j + 1]) { // swap temp and arr[i] int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } /* Prints the array */ static void printArray(int []arr) { int n = arr.Length; for (int i = 0; i < n; ++i) Console.Write(arr[i] + " "); Console.WriteLine(); } // Driver method public static void Main() { int []arr = {64, 34, 25, 12, 22, 11, 90}; bubbleSort(arr); Console.WriteLine("Sorted array"); printArray(arr); } } // This code is contributed by Sam007

• PHP

  <?php // PHP program for implementation // of Bubble Sort function bubbleSort(&$arr) { $n = sizeof($arr); // Traverse through all array elements for($i = 0; $i < $n; $i++) { // Last i elements are already in place for ($j = 0; $j < $n - $i - 1; $j++) { // traverse the array from 0 to n-i-1 // Swap if the element found is greater // than the next element if ($arr[$j] > $arr[$j+1]) { $t = $arr[$j]; $arr[$j] = $arr[$j+1]; $arr[$j+1] = $t; } } } } // Driver code to test above $arr = array(64, 34, 25, 12, 22, 11, 90); $len = sizeof($arr); bubbleSort($arr); echo "Sorted array :
"; for ($i = 0; $i < $len; $i++) echo $arr[$i]." "; // This code is contributed by ChitraNayal. ?>

• JavaScript

  <script> function swap(arr, xp, yp) { var temp = arr[xp]; arr[xp] = arr[yp]; arr[yp] = temp; } // An optimized version of Bubble Sort function bubbleSort( arr, n) { var i, j; for (i = 0; i < n-1; i++) { for (j = 0; j < n-i-1; j++) { if (arr[j] > arr[j+1]) { swap(arr,j,j+1); } } } } /* Function to print an array */ function printArray(arr, size) { var i; for (i=0; i < size; i++) document.write(arr[i]+ " "); document.write("
"); } // Driver program to test above functions var arr = [64, 34, 25, 12, 22, 11, 90]; var n = 7; document.write("UnSorted array:
"); printArray(arr, n); bubbleSort(arr, n); document.write("Sorted array:
"); printArray(arr, n); </script>

Output:
Sorted array:
11 12 22 25 34 64 90

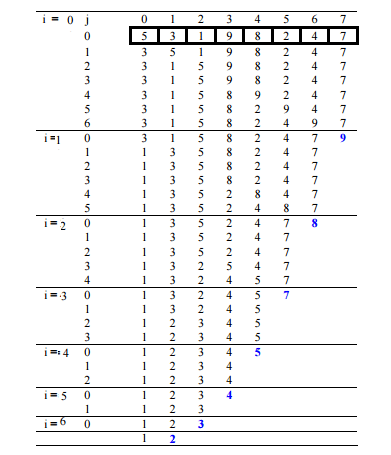Optimized implementation

The standard implementation always performs O(n²) comparisons even if the array becomes sorted before completing all passes. An important optimization is to track whether any swap happened during an inner loop; if no swap occurred the array is already sorted and the algorithm can stop early. This makes Bubble Sort adaptive: it runs faster on nearly-sorted arrays.

• CPP (Optimized)

  // Optimized implementation of Bubble sort #include <stdio.h> void swap(int *xp, int *yp) { int temp = *xp; *xp = *yp; *yp = temp; } // An optimized version of Bubble Sort void bubbleSort(int arr[], int n) { int i, j; bool swapped; for (i = 0; i < n-1; i++) { swapped = false; for (j = 0; j < n-i-1; j++) { if (arr[j] > arr[j+1]) { swap(&arr[j], &arr[j+1]); swapped = true; } } // IF no two elements were swapped by inner loop, then break if (swapped == false) break; } } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i=0; i < size; i++) printf("%d ", arr[i]); printf("
"); } // Driver program to test above functions int main() { int arr[] = {64, 34, 25, 12, 22, 11, 90}; int n = sizeof(arr)/sizeof(arr[0]); bubbleSort(arr, n); printf("Sorted array:
"); printArray(arr, n); return 0; }

• Java (Optimized)

  // Optimized java implementation // of Bubble sort import java.io.*; class GFG { // An optimized version of Bubble Sort static void bubbleSort(int arr[], int n) { int i, j, temp; boolean swapped; for (i = 0; i < n - 1; i++) { swapped = false; for (j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // swap arr[j] and arr[j+1] temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; swapped = true; } } // IF no two elements were swapped by inner loop, then break if (swapped == false) break; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) System.out.print(arr[i] + " "); System.out.println(); } // Driver program public static void main(String args[]) { int arr[] = { 64, 34, 25, 12, 22, 11, 90 }; int n = arr.length; bubbleSort(arr, n); System.out.println("Sorted array: "); printArray(arr, n); } } // This code is contributed by Nikita Tiwari.

• Python3 (Optimized)

  # Python3 Optimized implementation of Bubble sort # An optimized version of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): swapped = False # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1. Swap if the element # found is greater than the next element if arr[j] > arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] swapped = True # IF no two elements were swapped by inner loop, then break if swapped == False: break # Driver code to test above arr = [64, 34, 25, 12, 22, 11, 90] bubbleSort(arr) print ("Sorted array :") for i in range(len(arr)): print ("%d" %arr[i], end=" ") # This code is contributed by Shreyanshi Arun

• C# (Optimized)

  // Optimized C# implementation of Bubble sort using System; class GFG { // An optimized version of Bubble Sort static void bubbleSort(int []arr, int n) { int i, j, temp; bool swapped; for (i = 0; i < n - 1; i++) { swapped = false; for (j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // swap arr[j] and arr[j+1] temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; swapped = true; } } // IF no two elements were swapped by inner loop, then break if (swapped == false) break; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i < size; i++) Console.Write(arr[i] + " "); Console.WriteLine(); } // Driver method public static void Main() { int []arr = {64, 34, 25, 12, 22, 11, 90}; int n = arr.Length; bubbleSort(arr,n); Console.WriteLine("Sorted array"); printArray(arr,n); } } // This code is contributed by Sam007

• PHP (Optimized)

  <?php // PHP Optimized implementation of Bubble sort // An optimized version of Bubble Sort function bubbleSort(&$arr) { $n = sizeof($arr); // Traverse through all array elements for($i = 0; $i < $n; $i++) { $swapped = False; // Last i elements are already in place for ($j = 0; $j < $n - $i - 1; $j++) { // traverse the array from 0 to n-i-1. Swap if the element // found is greater than the next element if ($arr[$j] > $arr[$j+1]) { $t = $arr[$j]; $arr[$j] = $arr[$j+1]; $arr[$j+1] = $t; $swapped = True; } } // IF no two elements were swapped by inner loop, then break if ($swapped == False) break; } } // Driver code to test above $arr = array(64, 34, 25, 12, 22, 11, 90); $len = sizeof($arr); bubbleSort($arr); echo "Sorted array :
"; for($i = 0; $i < $len; $i++) echo $arr[$i]." "; // This code is contributed by ChitraNayal. ?>

Output:
Sorted array:
11 12 22 25 34 64 90

Time complexity, space and properties

• Worst and average case time complexity: O(n²). The worst case occurs when the array is reverse sorted; the average case is also quadratic.
• Best case time complexity: O(n). This occurs when the array is already sorted and the optimized version detects no swaps in the first pass and stops.
• Auxiliary space: O(1). Bubble Sort is an in-place algorithm; it requires only a constant amount of extra memory.
• Boundary cases: Bubble Sort takes minimum time (order of n) when elements are already sorted and the optimized early-exit is used.
• Stable: Yes. Bubble Sort preserves the relative order of equal elements.
• Sorting in place: Yes.
• Adaptive: The optimized version is adaptive - it performs fewer operations on nearly-sorted arrays.

When and where to use Bubble Sort

• Bubble Sort is primarily used as a teaching example to introduce fundamental sorting concepts such as comparisons, swaps and algorithm invariants.
• Because of its simplicity, it may be used on very small lists or in situations where simplicity of implementation matters more than performance.
• Bubble Sort can be useful in specialised contexts where the array is almost sorted and one expects only a few local inversions; the optimized variant will fix such small errors in near-linear time.
• Example application: in some polygon-filling algorithms in computer graphics, bounding edges are kept sorted by x-coordinate at scan lines. As the scan line moves, the order changes only at intersections; bubble-like swaps can update the order efficiently.

Notes for students

• Number of comparisons in the naive implementation is approximately n(n-1)/2 and the number of swaps depends on the number of inversions in the array.
• Bubble Sort is rarely used in production code because faster algorithms (quick sort, merge sort, heap sort, radix sort) are generally preferred; however, understanding bubble sort helps in grasping more advanced sorting techniques.
• Always use the optimized variant with a swapped flag if you expect nearly-sorted inputs; it is a minimal change that improves average behaviour significantly.

References & credits: Code contributors retained from source: rathbhupendra, Rajat Mishra, Shreyanshi Arun, Sam007, ChitraNayal, Nikita Tiwari, Nikita Tiwari, Rajat Mishra and others as shown near respective code blocks.