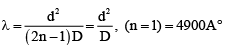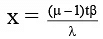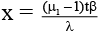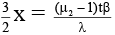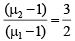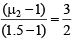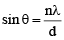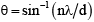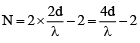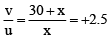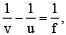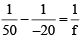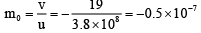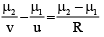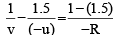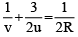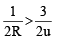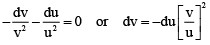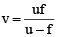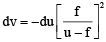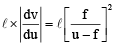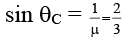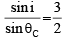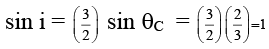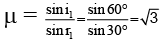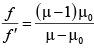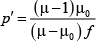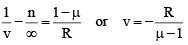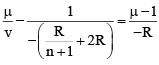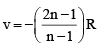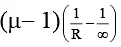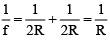JEE Advanced (Single Correct Type): Ray & Wave Optics | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. In Young’s double slit experiment, the width of fringe is obtained from a source of light of wavelength 5000A° is 3.9 mm. if the apparatus is immersed in a liquid of m = 1.3, the fringe width will be
(a) 2 mm
(b) 3 mm
(c) 4 mm
(d) 5 mm

Correct Answer is option (b)
Wavelength of light in the liquid is
λ' = l/m = 5000A°/1.3
Fringe width β' = Dλ' / d (in liquid) . . . (1)
β = Dλ / d (in air) . . . (2)
From (1) and (2) we have
β' = β/m = 3.9/1.3
= 3 mm

Q.2. In a simple Young’s double slit experiment the distance between the slits is 0.7 mm. The screen is at a distance 1 m from the slits. Monochromatic light is incident normally on the double slit. If a dark fringe is formed directly opposite a slit on the screen, the wavelength of radiation can have the value
(a) 4900 A°
(b) 9800 A°
(c) 49000 A°
(d) none of these

Correct Answer is option (a)
, where n is an integer.
⇒

Q.3. In Young's double slit experiment, the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the beams.  When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x.  The refractive index of the second plate is
(a) 1.75
(b) 1.50
(c)  1.25
(d) 1.00

Correct Answer is option (a)
The path difference introduced by a plate of thickness t and refractive index m is given by
Δ = (μ - 1) t
A path difference of l introduced a phase shift of β where β = λD/(2d)  . 2d  = separation between slits
So, a path difference of (μ - 1)t introduces a shift x on the screen given by

For first plate,
For second plate,
∴
⇒
⇒ μ₂ = 1.75

Q.4. Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d (<<R) symmetrically about the centre of the circle. The sources emit identical wavelength l .  The number of the points on the circle with maximum intensity is
(a) (2d/λ) +1
(b) 4d/λ
(c) (4d/λl)-2
(d) (4d/λ)+2

Correct Answer is option (c)
For maxima
⇒
For -π/2 ≤ θ ≤ π / 2
n = 2d / λ
Hence for 0 ≤ θ <2π total number of maxima

Q.5. A ray of light strikes a glass slab (R.I. = m) of finite thickness t. The emerging light is
(a) parallel to the incident ray
(b) perpendicular to the incident ray
(c) rotates by an angle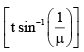
(d) totally internally reflected 

Correct Answer is option (a)

Q.6. An optical fiber uses the principle of
(a) diffraction of light
(b) absorption of light
(c) high transmission coefficient of the fiber material
(d) total internal reflection

Correct Answer is option (d)

Q.7. An object and a screen are mounted on an optical bench and a converging lens is placed between them so that a sharp image is obtained on the screen. The linear magnification of the image is 25. The lens is now moved 30 cm towards the screen and a sharp image is again formed on the screen. Find the focal length of the lens.
(a) 14.0 cm
(b) 14.3 cm
(c) 14.6 cm
(d) 14.9 cm

Correct Answer is option (b)
If O and I are the object and image, respectively, and L1 and L2 are the two conjugate positions of the lens,
then OL₁ = IL₂

⇒ 30 + x =  2.5x or x = 20 cm
From

or f = 14.3 cm

Q.8. A giant telescope in an observatory has an objective of focal length 19 m and an eye-piece of focal length 1.0 cm. What is the diameter of the image of moon formed by the objective in normal adjustment? The diameter of moon is 3.5 x10⁶ m and the radius of the lunar orbit round the earth is 3.8 x 10⁸ m.
(a) 10 cm
(b) 12.5 cm
(c) 15 cm
(d) 17.5 cm

Correct Answer is option (d)
As u >> f₀, v = f₀ = 19 m
Now, u = -3.8 x 10⁸ m.
Therefore, magnification produced by the objective is

∴ Diameter of the image of moon = 3.5 x 10⁶ x  0.5 x 10^-7 = 0.175 m = 17.5 cm. 

Q.9. A soldier directs a laser beam on an enemy by reflecting the beam from a mirror. If the mirror is rotated by an angle q, by what angle will the reflected beam rotate?
(a) θ/2
(b) θ
(c) 2θ
(d) None of these 

Correct Answer is option (c)
Let M₁OM₂ be the initial position of the mirror. The mirror is rotated through an angle θ to the positionM'₁;OM'₂. PO is the incident light. OQ was the initial reflected ray and OQ' is the reflected ray after rotating the mirror by angle θ. If i = initial incidence angle, then ∠POQ = 2i and
∠POQ' = ∠PON'+ ∠N'OQ = 2i - 2θ
∴ The reflected beam rotates through an angle 2θ.

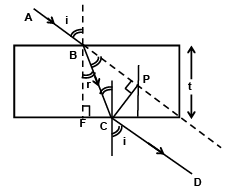
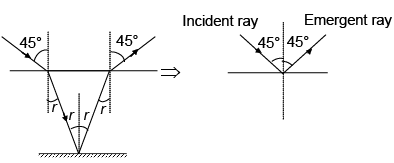
Q.10. One side of the glass slab is silvered as shown. A ray of light is incident on the other side at an angle of incidence i = 45°. Refractive index of glass is given as 1.5. The deviation of the ray of light from its initial path when it comes out of the slab is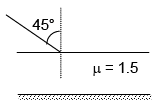
(a) 90°
(b) 180°
(c) 120°
(d) 45° 

Correct Answer is option (a)
From the figure it is clear that the angle between incident ray and the emergent ray is 90°.

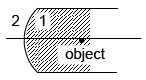
Q.11. Refraction takes place at a concave spherical boundary separating glass air medium. For the image to be real, the object distance (μ_g = 3/2)
(a) should be greater than three times the radius of curvature of the refracting surface.
(b) should be greater than two times the radius of curvature of the refracting surface.
(c) should be grater than the radius of curvature of the refracting surface.
(d) is independent of the radius of curvature of the refracting surface.

Correct Answer is option (a)
Applying

or  
for v to be positive,
or u >3 R

Q.12. A short linear object of length l lies along the axis of a concave mirror of focal length f at a distance u from the pole. What is the size of the image?
(a)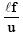
(b)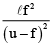
(c)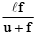
(d)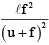

Correct Answer is option (b)
According to mirror formula, we have
 ...(1)
Now, as for a given mirror, f = constant.
∴
But from Eq. (1),

So,

∴ Image size =

Q.13. A fish is swimming in a pool whose bottom surface is silver polished. Find where an observer in the air will observe the image of the fish if the depth of the pool is H and the fish is at depth h below the water surface?
(a) (H - h)/μ
(b) 2(H - h)/μ
(c) (H + h)/μ
(d) (2H - h)/μ

Correct Answer is option (d)
The ray diagram is shown. From the figure, it is clear that the image of the fish forms at depth H -h below the mirror.
⇒ The depth of the image = H + H - h = 2H - h
Therefore, the apparent depth of the image as seen by an observer in air = (2H-h)/μ 

Q.14. A point source of light B is placed at a distance L in front of the centre of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown. The greatest distance over which he can see the image of the light source in the mirror is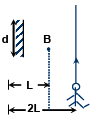
(a) d/2
(b) d
(c) 2d
(d) 3d

Correct Answer is option (d)
In similar Δ ABI & ΔMNI
MN/AB = IQ/IP
⇒ MN = (3L/L)(D) = 3d 

Q.15. A ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray, which enters the sphere, the rays comes out tangentially from the surface of the sphere?
(a) tan^–1 (2/3)
(b) sin^–1(2/3)
(c) 90°
(d)cos^–1 (1/3) 

Correct Answer is option (c)
∠ ABO = ∠ OAB = θ_C

Applying snell’s law at A  


or    i = 90°

Q.16. One of the refracting surfaces of a prism of angle 30° is silvered. A ray of light incident at an angle of 60° retraces its path. The refractive index of the material of prism is
(a) √2
(b) √3
(c) 3/2
(d) 2 

Correct Answer is option (b)
r₂ = 0°
∴ r₁ = A =30°
and i₁ = 60°
∴

Q.17. A lens has focal length f in air. If refractive index of its material is m, what is its power when immersed in liquid of refractive index μ₀?
(a)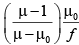
(b)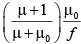
(c)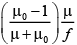
(d)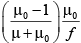

Correct Answer is option (a)
in air
 in water
So,
⇒

Q.18. A ray of light is incident normally on one face of an equilateral prism of refractive index 1.5. The angle of deviation is
(a) 30°
(b) 45°
(c) 60°
(d) 75°

Correct Answer is option (c)
r' = 60°. If refraction is to take place at the second surface, then

Since sin i' > 1, total internal reflection takes place at AC.
∠ BPC = 90°, therefore no further deviation takes place at BC.
Thus, total deviation = 180° - 120° = 60°

Q.19. A parallel beam of light travelling in water (μ = 4/3)  is refracted by a spherical bubble of radius R = 1 mm. Assuming the light rays to be paraxial, the position of the final image from the centre is
(a) 2 mm to the left
(b) 4 mm to the left
(c) 5 mm to the right
(d) 8 mm to the left 

Correct Answer is option (b)
For refraction at the first surface,

This acts as object for the second surface.
Now, we have

or
Thus, final image is formed at  = 4 mm to the left from the centre.

Q.10. Two plano-convex lenses of radius of curvature R and R.I. 1.5 will have a combined focal length equal to R when they are placed
(a)at distance R/4 apart
(b) at distance R/2 apart
(c)at distance R apart
(d) in contact with each other

Correct Answer is option (d)
Focal length of each lens =
⇒
When placed in contact