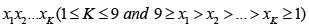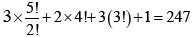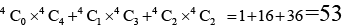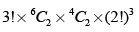JEE Advanced (Single Correct Type): Permutations & Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The value of P(n, n-1) is
(a) n
(b) n!
(c) 2n
(d) 2n!
Correct Answer is option (b)
We know that P(n, r) = nPr = n!/(n-r)!
Hence, P(n, n-1) = nPn-1 = n!/[n-(n-1)]!
P(n, n-1) = n!/(n-n+1)! = n!/1! = n!
Therefore, the value of P(n, n-1) is n!.
Hence, the correct answer is option (b) n!
Q.2. The number of ways in which 8 students can be seated in a line is
(a) 5040
(b) 50400
(c) 40230
(d) 40320
Correct Answer is option (d)
For the 1st position, there are 8 possible choices. For the 2nd position, there are 7 possible choices. For the 3rd position, there are 7 possible choices, etc. And for the eighth position, there is only one possible choice. Hence, this can be written as 8!
(i.e.) 8! = 8×7×6×5×4×3×2×1=40,320
Hence, the number of ways in which 8 students can be seated in a line is 40320.
Q.3. If nP5 = 60n−1P3, the value of n is
(a) 6
(b) 10
(c) 12
(d) 16
Correct Answer is option (b)
Given that nP5 = 60n−1P3
We know that P(n, r) = nPr = n!/(n-r)!
Now, apply the formula on both sides to get the value of n.
n!/(n-5)! = 60 [(n-1)!/[(n-1)-3]!]
On solving the above equation, we get n= -6 and n=10.
Since the value of n cannot be negative, the value of n is 10.
Hence, option (b) 10 is the correct answer.
Q.4. The number of squares that can be formed on a chessboard is
(a) 64
(b) 160
(c) 204
(d) 224
Correct Answer is option (c)
1×1 grid squares = 8×8 = 64, 2×2 grid squares = 7×7 = 49, 3×3 grid squares = 6×6 = 36 upto 8×8 grid squares = 1×1 = 1.
Hence, the total number of squares that can be formed on a chess board = 82+72+62+…+12
= 12+22+32+…+82
= [n(n+1)(2n+1)]/6
Here, n=8
Hence,
= [8(8+1)(16+1)]/6
= (8×9×17)/6
= 12×17 = 204
Hence, option (c) 204 is the correct answer.
Q.5. The number of ways 4 boys and 3 girls can be seated in a row so that they are alternate is
(a) 12
(b) 104
(c) 144
(d) 256
Correct Answer is option (c)
Given that, there are 4 boys and 3 girls.
The only pattern 4 boys and 3 girls are arranged in an alternate way is BGBGBGB.
Therefore, the total number of ways is 4!×3! = 144.
Q.6. The number of ways 10 digit numbers can be written using the digits 1 and 2 is
(a) 210
(b) 10C2
(c) 10!
(d) 10C1+9C2
Correct Answer is option (a)
Given digits are 1 and 2.
Here, each place can be filled in two ways either with 1 or 2 and every place has two chances.
Therefore, the number of ways 10 digit numbers can be written using the digits 1 and 2 is 210.
Hence, option (a) 210 is the correct answer.
Q.7. A coin is tossed n times, the number of all the possible outcomes is
(a) 2n
(b) 2n
(c) C(n, 2)
(d) P(n, 2)
Correct Answer is option (b)
We know that, when a coin is tossed, we will get either head or tail.
Therefore, the number of all possible outcomes when a coin is tossed n times is 2n.
Q.8. In how many ways 8 distinct toys can be distributed among 5 children?
(a) 8P5
(b) 5P8
(c) 58
(d) 85
Correct Answer is option (c)
Given that, the number of toys = 8
The number of children = 5.
Hence, the number of ways 8 distinct toys can be distributed among 5 children is
5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 = 58.
Hence, option (c) 58 is the correct answer.
Q.9. There are 10 true-false questions in an examination. These questions can be answered in:
(a) 20 ways
(b) 100 ways
(c) 512 ways
(d) 1024 ways
Correct Answer is option (d)
Given that there are 10 questions.
Each question can be answered in two ways. (i.e. either true or false).
Hence, the number of ways these questions can be answered is 210, which is equal to 1024.
Q.10. In how many ways can we paint the six faces of a cube with six different colours?
(a) 30
(b) 6
(c) 6!
(d) None of the above
Correct Answer is option (a)
Now, let us consider the 6 different colours: c1, c2, c3, c4, c5, c6.
Assume that the face of the cube facing up is c1. So, the face of the cube at the bottom can be painted in 5 different ways.
So, 4 faces on the horizontal side of the cube are in circular permutation and they can be painted in (4 - 1)! ways.
Hence, the total number of ways we can paint the faces of a cube with six different colours is 5 × (4 - 1)! ways.
Hence, 5 × (4 - 1)! ways = 5 × 3! = 5 × 3 × 2 × 1 = 30 ways.
Q.11. Sum of all the five digits natural numbers formed using all the digits {0, 1, 2, 3, 4}
(a) 2599980
(b) 2666640
(c) 1999980
(d) none of these
Correct Answer is option (a)
Sum of all the number is 10 × 24 × 104 + 10 × 18 × 103 + 10 × 18 × 102 + 10 × 18 × 10 + 10 × 18 × 1. = 2599980
Q.12. The no. of rational numbers lying in the interval (2002, 2003) all whose digits after the decimal point are non-zero and are in decreasing order
(a) 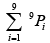
(b) 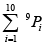
(c) 29 -1
(D) 210 -1
Correct Answer is option (c)
A rational number of the desired category is of the form 2002.
= 9C1 + 9C2 + ...... + 9C9 = 29 -1
Q.13. There are four pairs of shoes of different sizes. Each of the 8 shoes can be coloured with one of the four colours : Black, Brown, White and Red. The number of ways the shoes can be coloured so that in atleast three pairs, the left shoe and the right shoe do not have the same colour is
(a) 124
(b) 28 x 123
(c) 16 x 123
(d) 4 x 123
Correct Answer is option (b)
We discuss two disjoint possibilities
Case -1 : In Exactly three pairs the shoes of a pair have opposite colours. The number of ways this occur is 16 x 123.
Case-2 : In Each one of the four pairs the left and right shoes have opposite colours. This can occur is 124 ways.
Q.14. The letters of the word “DRAWER” are arranged in alphabetical order. The number of arrangements that precede the word “ REWARD” is
(a) 241
(b) 242
(c) 247
(d) 248
Correct Answer is option (c)
The letters of the word ‘DRAWER’ in alphabetical order are A, D, E, R, R and W. The number of words that precede the word “REWARD” is
Q.15. The number of four digit numbers that can be formed using the digits 1,2,3,4,5,6 that are divisible by 3,when repetition of digits is allowed, is
(a) 23 x 32
(b) 23 x 33
(c) 23 x 34
(d) 24 x 33
Correct Answer is option (d)
The first 3 digits can be filled in 63 ways. After filling the first 3 digits, the last digit can be filled using 1, 2, 3, 4, 5, 6 in 6 ways. But the six numbers so formed are consecutive integers out of which only two are divisible by 3. Hence the number of choices = 2 x 63 = 24 x 33
Q.16. Let S = {1, 2, 3, ...100} . The number of non-empty subsets A of S such that the product of elements in A is even is
(a) 250(250 -1)
(b) 2100 -1
(c) 250 -1
(d) 2100 -275
Correct Answer is option (a)
Total number of non-empty subsets of S is 2100 -1. Total no.of non empty subsets of S in which each elements is odd is 250 -1
∴Required number = ( 2100 -1) - ( 250 -1)
Q.17. Let A be the set of 4-digit numbers a1a2a3a4 where a1 > a2 > a3 >a4 , then n(A) is equal to
(a) 126
(b) 84
(c) 210
(d) none of these
Correct Answer is option (c)
Any selection of four digits from the ten digits 0, 1, 2, 3, ... 9 gives one such number. SO, the required number of numbers = 10C4
= 210.
Q.18. The number of 5 digit numbers that contain 7 exactly once is
(a) 41 (93)
(b) 37 (93)
(c) 7 (94)
(d) 41 (94)
Correct Answer is option (a)
5 digit numbers having 7 in 1st place = 94
In 2nd, 3rd, 4th, 5th places is 4 x 8 x 93
Total number of 5 digit numbers having 7 exactly once is = 41 (93).
Q.19. 4 points out of 8 points in a plane are collinear. Number of different quadrilateral that can be formed by joining them is
(a) 56
(b) 53
(c) 76
(d) 60
Correct Answer is option (b)
Number of ways = (collinear (o) and non collinear (40))
OR (collinear (1) and non collinear (3))
OR (collinear (2) and non collinear (2))
=
Q.20. Four men and six women are to be seated along a round table. The number of cases where every two men are separated by two women is
(a) 3420
(b) 4320
(c) 1710
(d) None of these
Correct Answer is option (b)
4 men may be seated in 3! Ways.
The pairs of women can be selected in 6C24C2 ways
The numbers of arrangements is
= 6 15 6 8 4320 ways
|
446 docs|929 tests
|