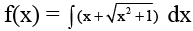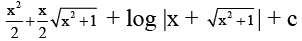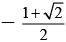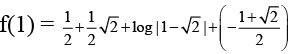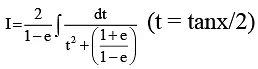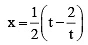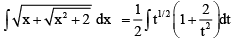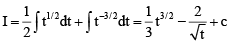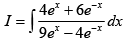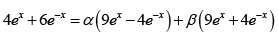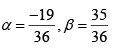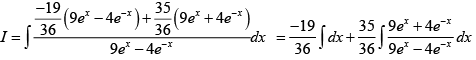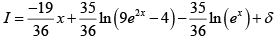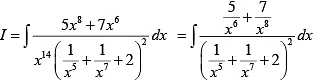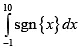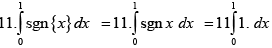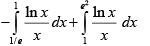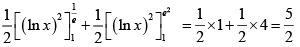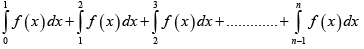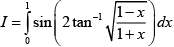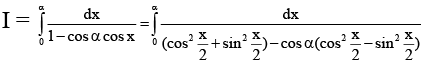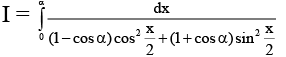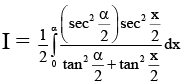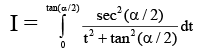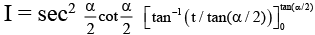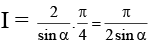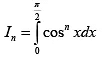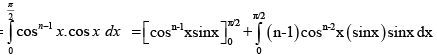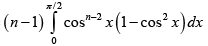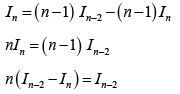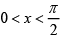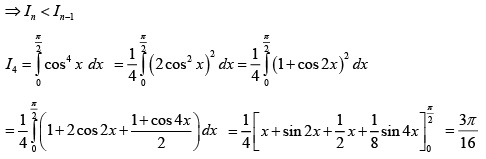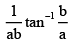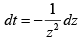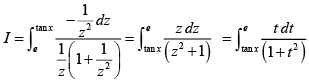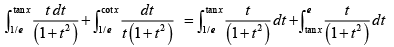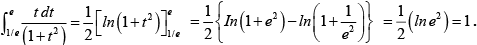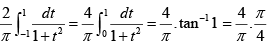JEE Advanced (One or More Correct Option): Indefinite Integral | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If f'(x) = 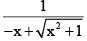 and f(0) =  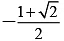, then f(1) is equal to
(a) - log ( √2 - 1)
(b) 1
(c) 1 + √2
(d) log (1 + √2 )

Correct Answer is options (a, d)

=
Putting x = 0, f(0) = c so c =
and
= log (1 + √2 ) = - log ( √2 - 1)

Q.2. The value of 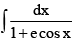 must be same as
(a) 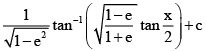(e lies between 0 and 1)
(b) 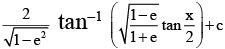, (e lies between 0 and 1)
(c) 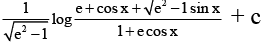 , (e is greater than 1)
(d) , (e is greater than 1)

Correct Answer is options (b, c)

If  So,  (B) is correct
If  So, (C) is correct. 

Q.3. If 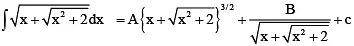, then
(a) A = 1/3
(b) B = -2
(c) A = 2/3
(d) B = -1

Correct Answer is options (a, b)

⇒ x² + 2 = t² + x² – 2tx
⇒
So

Q.4. If 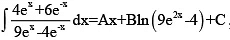, then
(a) A = 3/2
(b) B = 35/36
(c) C is indefinite
(d) A + B = -19/36

Correct Answer is options (b, c, d)

We write  
So 9α + 9β = 4 -4α + 4β = 6

∴
=  ,  where  δ is integration constant

=
On comparing with I = Ax + B ln (9e^2x - 4) + C
 is indefinite

Q.5. If 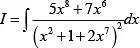 then I is equal to
(a)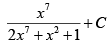
(b)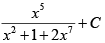
(c)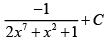
(d)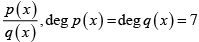

Correct Answer is options (a, d)
We can write

Put  so that

Q.6. Which of the following options is/are correct?
(a) 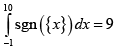 , where { x} is fractional part of x .
(b)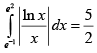
(c)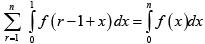
(d)

Correct Answer is options (b, c)

=
= 11

=
=

=
=
=

put x = cosθ ⇒ dx = - sinθ dθ

Q.7. If 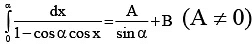. Then possible values of A and B are
(A) A = π/2, B = 0
(B) A = π/4, B = π/4sinα
(C) A = π/6, B = π/sinα
(D) A = π, B = π/sinα

Correct Answer is options (a, b)



Put tan x/2 =  t



Thus,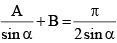  
⇒ A = 2π, B = 0 and A = π/4, B = π/4sinα Satisfy the last equation.

Q.8. Let 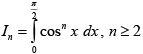 is natural number,  then
(a)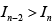
(b)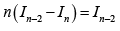
(c)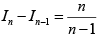
(d)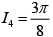

Correct Answer is options (a, b)

=
=

Clearly I_{n-2 >} I_n
Also for
0 < cos x < 1
So, cosⁿx < cos^n-1x

Q.9. The value of the integral 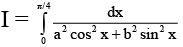 is
(a)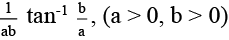
(b)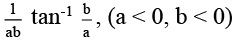
(c)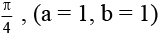
(d)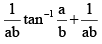

Correct Answer is options (a, b, c)
 [for a = 1, b = 1]
Also,  (t = tanx)
=  (a ≠ 0, b ≠ 0)
=

Q.10. The value of 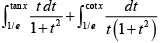 is
(a)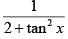
(b) 1
(c) π/4
(d)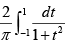

Correct Answer is options (b, d)
Let  Put t = 1/z
∴
∴
∴
=
Also,
= 1