Frequency Response Analysis of Second Order Control System | Control Systems - Electrical Engineering (EE) PDF Download
What is Frequency Response?
- The response of a system can be partitioned into both the transient response and the steady state response. We can find the transient response by using Fourier integrals. The steady state response of a system for an input sinusoidal signal is known as the frequency response. In this chapter, we will focus only on the steady state response.
- If a sinusoidal signal is applied as an input to a Linear Time-Invariant (LTI) system, then it produces the steady state output, which is also a sinusoidal signal. The input and output sinusoidal signals have the same frequency, but different amplitudes and phase angles.
Let the input signal be −
r(t) = A sin(ω0t)
The open loop transfer function will be −
G(s) = G(jω)
We can represent G(jω) in terms of magnitude and phase as shown below.
G(jω) = |G(jω)|∠G(jω)
Substitute, ω = ω0 in the above equation.
G(jω0) = |G(jω0)|∠G(jω0)
The output signal is
c(t) = A|G(jω0)|sin(ω0t + ∠G(jω0))
- The amplitude of the output sinusoidal signal is obtained by multiplying the amplitude of the input sinusoidal signal and the magnitude of G(jω) at ω = ω0.
- The phase of the output sinusoidal signal is obtained by adding the phase of the input sinusoidal signal and the phase of G(jω) at ω = ω0.
Where,
- A is the amplitude of the input sinusoidal signal.
- ω0 is angular frequency of the input sinusoidal signal.
We can write, angular frequency ω0 as shown below.
- ω0 = 2πf0
Here, f0 is the frequency of the input sinusoidal signal. Similarly, you can follow the same procedure for closed loop control system.
Frequency Domain Specifications
The frequency domain specifications are resonant peak, resonant frequency and bandwidth. Consider the transfer function of the second order closed loop control system as,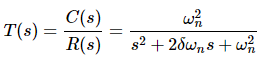
Substitute, s = jω in the above equation.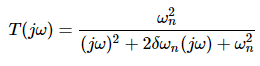
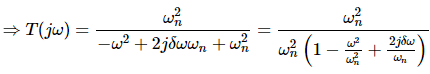
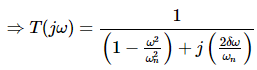
Let, ω/ωn = u Substitute this value in the above equation.
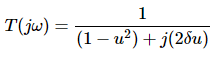
Magnitude of T(jω) is -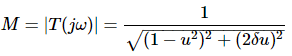
Phase of T(jω) is -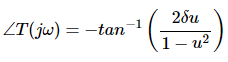
Resonant Frequency
It is the frequency at which the magnitude of the frequency response has peak value for the first time. It is denoted by ωr. At ω = ωr, the first derivate of the magnitude of T(jω) is zero.
Differentiate M with respect to u.
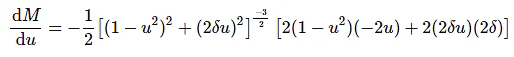
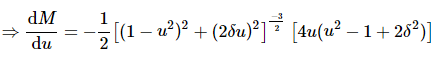
Substitute, u = ur and dM/du == 0 in the above equation.
⇒ 4ur(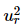 −1 + 2δ2) = 0
−1 + 2δ2) = 0
⇒ 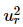 −1 + 2δ2 = 0
−1 + 2δ2 = 0
⇒ 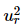 = 1−2δ2
= 1−2δ2
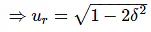
Substitute, ur = ωr/ωn in the above equation.
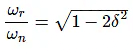
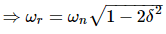
Resonant Peak
It is the peak (maximum) value of the magnitude of T(jω). It is denoted by Mr.
At u = ur, the Magnitude of T(jω) is -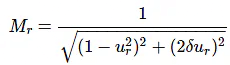
Substitute, 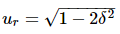 and 1−
and 1−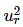 =2δ2 in the above equation.
=2δ2 in the above equation.
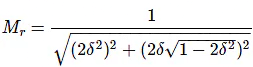
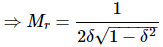
Resonant peak in frequency response corresponds to the peak overshoot in the time domain transient response for certain values of damping ratio δ. So, the resonant peak and peak overshoot are correlated to each other.
Bandwidth
It is the range of frequencies over which, the magnitude of T(jω) drops to 70.7% from its zero frequency value.
At ω=0, the value of u will be zero.
Substitute, u = 0 in M.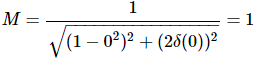
Therefore, the magnitude of T(jω) is one at ω=0.
At 3-dB frequency, the magnitude of T(jω) will be 70.7% of magnitude of T(jω) at ω = 0.
i.e., at ω = ωB, M = 0.707(1) = 1/√2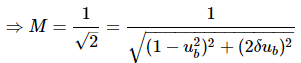
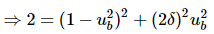
Let, 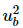 = x
= x
⇒ 2 = (1 − x)2 + (2δ)2x
⇒ x2 + (4δ2 − 2)x − 1 = 0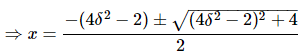
Consider only the positive value of x.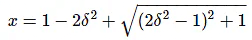

Substitute, 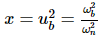
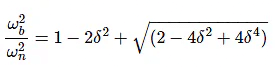
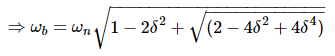
Bandwidth ωb in the frequency response is inversely proportional to the rise time tr in the time domain transient response.
|
54 videos|83 docs|40 tests
|
















