Quadrature Amplitude Modulation (QAM) | Communication System - Electronics and Communication Engineering (ECE) PDF Download
Introduction
QAM is similar to Double Sideband Modulation Suppressed Carrier (DSBSC), generating two sidebands symmetric to the carrier frequency. It sends two message signals over the same spectrum.
QAM has applications in various fields, including in today's technology. The example of QAM in analog modulation is PM (Phase Modulation), where the signal's amplitude is constant, and the phase varies. Another example is PSK (Phase Shift Keying) in digital modulation, where also the phase of the signal varies. But, QAM using Shift keying has greater applications in digital communication to transmit a high number of bits over the same spectrum.
Quadrature refers to the phase shift of 90 degrees. It means four and is derived from 360 degrees/4 = 90 degrees. The components used in the modulation are cosine waves and sine waves, which differ by a phase shift of 90 degrees.
These two waves are shown below: The upper wave is the sine wave, and the lower is the cosine wave.
The upper wave is the sine wave, and the lower is the cosine wave.
QAM is a family of analog modulation as well as digital modulation. It can be used to vary the amplitudes in analog modulation and two digital bitstreams using ASK (Amplitude Shift Keying) in digital modulation. Here, we will discuss QAM based on the analog modulation.
QAM Modulator
Unlike DSB, Quadrature Amplitude Modulation sends two message signals over the same spectrum. The first message signal is sent by multiplying it with the carrier signal.
m1(t) = The first message signal
cosωct = The first carrier signal
Product = m1(t)cosωct
The second message signal is sent in Quadrature. The message signal is multiplied by sinωct.
m2(t) = The first message signal
sinωct = Quadrature carrier signal
Product = m2(t)sinωct
Quad means four. The Quadrature carrier signal means a phase shift of 90 degrees. It means that both the carrier signals differ by a phase shift of 90 degrees.
cos (90 - ωct) = sinωct or sin (90 - ωct) = cosωct
The product of both the signals is further added. It is given by:
MQ (t) = m1(t)cosωct + m2(t)sinωct
The process of multiplication of the message signal and the carrier signal is known as mixing or modulation.
The block diagram of a simple analog Quadrature Amplitude Modulation is shown below: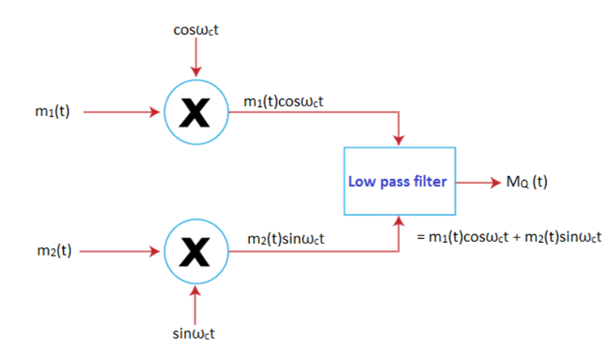
QAM Demodulator
Demodulation is the reverse process of modulation. It recovers the original signal from the product to make it available to the receiver. Here, the demodulation is based on the coherent detection method. The carrier is multiplied with the output of the modulator and then applied to the low pass filter. QAM does not have carrier with the signal like DSBSC transmission. Hence, the carrier is selected, which is coherent with the original baseband signal to prevent further phase shifts and distortion.
It is given by:
MQ x (carrier signal) = (m1(t)cosωct + m2(t)sinωct) x (carrier signal)
The carrier signal can be cosωct or its Quadrature sinωct. Let's discuss both the possibilities of the carrier signal.
- If MQ is multiplied with cosωct, we get the first signal m1(t) back. Thus, it helps to recover the first message signal.
MQ x cosωct = (m1(t)cosωct + m2(t)sinωct) x cosωct
MQ cosωct = m1(t)cos2ωct + m2(t)sinωctcosωct
MQ cosωct = 1/2 [(1 + cosωct) m1(t) + m2(t)sin2ωct]
MQ cosωct = 1/2 [m1(t) + cosωct m1(t) + m2(t)sin2ωct] - If MQ is multiplied with sinωct, we get the signal m2(t) back. Thus, it helps to recover the second message signal.
MQ x sinωct = (m1(t)cosωct + m2(t)sinωct) x sinωct
MQ sinωct = m1(t)cosωct sinωct + m2(t)sin2ωct
MQ cosωct = 1/2 [m1(t) sin2ωct + m2(t) - m2(t)cos2ωct]
The function of a low pass filter is to allow a certain band of frequencies to pass through it. In QAM, a low pass filter brings out the message signals m1(t) and m2(t) by suppressing the components around the frequency 2ωc.
The block diagram of the QAM demodulator is shown below:
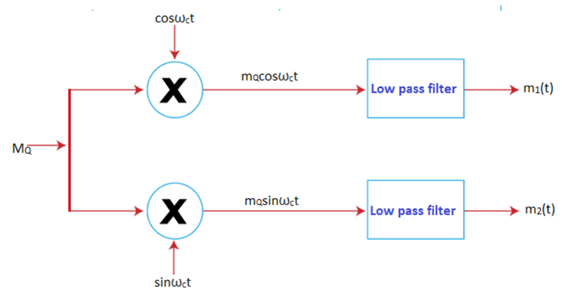 QAM can give the performance like Single Sideband (SSB) transmission if there is no phase error. It is because a phase error can result in co-channel interference. In practical communication, carrier synchronization is maintained by sending the carrier in between messages. It prevents interference in the channel.
QAM can give the performance like Single Sideband (SSB) transmission if there is no phase error. It is because a phase error can result in co-channel interference. In practical communication, carrier synchronization is maintained by sending the carrier in between messages. It prevents interference in the channel.
 |
Test: Single Sideband (SSB) Modulation
|
Start Test |
Advantages of QAM
The advantages of the Quadrature Amplitude Modulation are as follows:
- Increased bandwidth: QAM has a bandwidth greater than DSBSC because it can transmit two signals on the same spectrum.
- Low noise interference: QAM has low noise interference because the two signals are close together and requires a low noise to transmit the signal from one point to another.
Disadvantages of QAM
The disadvantages of Quadrature Amplitude Modulation are as follows:
- Complex Receiver: The receiver of QAM is complex because it needs two carrier signals of opposite phases to recover two message signals.
- Consumes more power: The requirement of additional amplifiers and filters increases its power consumption.
|
13 videos|39 docs|30 tests
|















