Types of Functions | Mathematics for Digital SAT PDF Download

Different Types of Functions

The function y = f(x) is classified into different types of functions, based on factors such as the domain and range of a function, and the function expression. The functions have a domain x value that is referred as input. The domain value can be a number, angle, decimal, fraction. Similarly, the y value or the f(x) value (is generally a numeric value) is the range. The types of functions have been classified into the following four types.

• Based on the Set Elements
• Based on Equation
• Based on Range
• Based on Domain

Representation of Functions

There are three different forms of representation of functions. The functions need to be represented to showcase the domain values and the range values and the relationship between them. 

• Venn Diagram: The Venn diagram is an important format for representing the function. The Venn diagrams are usually presented as two circles with arrows connecting the element in each of the circles. The domain is presented in one circle and the range values are presented in another circle. And the function defines the arrows, and how the arrows connect the different elements in the two circles.
• Graphical Form: Functions are easy to understand if they are represented in the graphical form with the help of the coordinate axes. Representing the function in graphical form, helps us to understand the changing behavior of the functions if the function is increasing or decreasing. The domain of the function - the x value is represented along the x-axis, and the range or the f(x) value of the function is plotted with respect to the y-axis.
• Roster Form: Roster notation of a set is a simple mathematical representation of the set in mathematical form. The domain and range of the function are represented in flower brackets with the first element of a pair representing the domain and the second element representing the range. Let us try to understand this with the help of a simple example. For a function of the form f(x) = x2, the function is represented as {(1, 1), (2, 4), (3, 9), (4, 16)}. Here the first element is the domain or the x value and the second element is the range or the f(x) value of the function.

List of Types of Functions

The types of functions are classified further to help for easy understanding and learning. The types of functions have been further classified into four different types, and are presented as follows.

1. Types of Functions - Based on Set Elements
These types of functions are classified based on the number of relationships between the elements in the domain and the codomain. The different types of functions based on set elements are as follows.

• One One Function: A one-to-one function is defined by f: A → B such that every element of set A is connected to a distinct element in set B. The one-to-one function is also called an injective function. Here every element of the domain has a distinct image or co-domain element for the given function.
• Many to One Function: A many to one function is defined by the function f: A → B, such that more than one element of the set A are connected to the same element in the set B. In a many to one function, more than one element has the same co-domain or image. If a many to one function, in the codomain, is a single value or the domain element are all connected to a single element, then it is called a constant function.
  
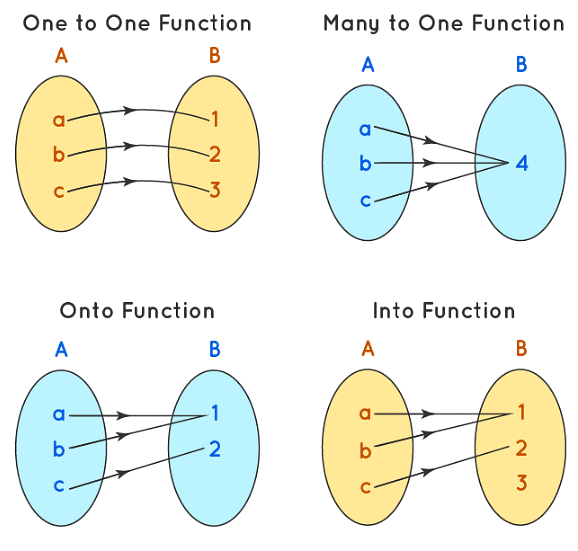
• Onto Function: In an, onto function, every codomain element is related to the domain element. For a function defined by f: A → B, such that every element in set B has a pre-image in set A. The onto function is also called a subjective function.
• One One and Onto Function (Bijection): A function that is both a one and onto function is called a bijective function. Here every element of the domain is connected to a distinct element in the codomain and every element of the codomain has a pre-image. Also in other words every element of set A is connected to a distinct element in set B, and there is not a single element in set B which has been left out.
• Into Function: Into function is exactly opposite in properties to an onto function. Here there are certain elements in the co-domain that do not have any pre-image. The elements in set B are excess and are not connected to any elements in set A.
• Constant Function: A constant function is an important form of a many to one function. In a constant function, all the domain elements have a single image. The constant function is of the form f(x) = K, where K is a real number. For the different values of the domain(x value), the same range value of K is obtained for a constant function.

2. Types of Function - Based on Equation

• The algebraic expressions are also functions and are based on the degree of the polynomial. The functions based on equations are classified into the following equations based on the degree of the variable 'x'.
  • The polynomial function of degree zero is called a Constant Function.
  • The polynomial function of degree one is called a Linear Function.
  • The polynomial function of degree two is called a Quadratic Function.
  • The polynomial function of degree three is a Cubic Function.

Identity Function

• The identity function has the same domain and range. The identity function equation is f(x) = x, or y = x. The domain and range of the identity function is of the form {(1, 1), (2, 2), (3, 3), (4, 4).....(n, n)}.
• The graph of the identity function is a straight line that is equally inclined to the coordinate axes and is passing through the origin. The identity function can take both positive and negative values and hence it is present in the first and the third quadrants of the coordinate axis.

Linear Function

• A polynomial function having the first-degree equation is a linear function. The domain and range of a linear function is a real number, and it has a straight line graph. Equations such as y = x + 2, y = 3x, y = 2x - 1, are all examples of linear functions. The identity function of y = x can also be considered a linear function.
• The general form of a linear function is f(x) = ax + b, is used to represent objective functions in linear programming problems. Here x, y are variables, and  a, b are real numbers. Graphically the linear function can be represented by the equation of a line y = mx + c, where m is the slope of the line and c is the y-intercept of the line.

Quadratic Function

• A quadratic function has a second-degree quadratic equation and it has a graph in the form of a curve. The general form of the quadratic function is f(x) = ax² + bx + c, where a ≠ 0 and a, b, c are constant and x is a variable. The domain and range of the quadratic function is R.
• The graph of a quadratic equation is a non-linear graph and is parabolic in shape. Examples of quadratic functions are f(x) = 3x² + 5, f(x) = x² - 3x + 2.

Cubic Function

• A cubic function has an equation of degree three. The general form of a cubic function is f(x) = ax³ + bx² + cx +d, where a ≠ 0 and a, b, c, and d are real numbers & x is a variable. The domain and range of a cubic function is R.
• The graph of a cubic function is more curved than the quadratic function. An example of cubic function is f(x) = 8x³ + 5x² + 3.

Polynomial Function

• The general form of a polynomial function is f(x) = aⁿxⁿ + a^n-1x^n-1 + a^n-2x^n-2+ ..... ax + b. Here n is a nonnegative integer and x is a variable. The domain and range of a polynomial function are R. Based on the power of the polynomial function, the functions can be classified as a quadratic function, cubic function, etc.

3. Types of Functions - Based on Range
Here the types of functions have been classified based on the range which is obtained from the given functions. The different types of functions based on the range are as follows.

• Modulus Function: The modulus function gives the absolute value of the function, irrespective of the sign of the input domain value. The modulus function is represented as f(x) = |x|. The input value of 'x' can be a positive or a negative expression. The graph of a modulus function lies in the first and the second quadrants since the coordinates of the points on the graph are of the form (x, y), (-x, y).
• Rational Function: A function that is composed of two functions and expressed in the form of a fraction is a rational function. A rational fraction is of the form f(x)/g(x), and g(x) ≠ 0. The functions used in this rational function can be an algebraic function or any other function. The graphical representation of these rational functions is similar to the asymptotes, since it does not touch the axis lines.
• Signum Function: The signum function helps us to know the sign of the function and does not give the numeric value or any other values for the range. The range of the signum function is limited to {-1, 0, 1}. For the positive value of the domain, the signum function gives an answer of 1, for negative values the signum function gives an answer of -1, and for the 0 value of a domain, the image is 0. The signum function has wide application in software programming.
• Even and Odd Function: The even and odd functions are based on the relationship between the input and the output values of the function. For the negative domain value, if the range is a negative value of the range of the original function, then the function is an odd function. And for the negative domain value, if the range is the same as that of the original function, then the function is an even function.
  If f(-x) = f(x), for all values of x, then the function is an even function, and if f(-x) = -f(x), for all values of x, then the function is an odd function. An example of even functions are x2, Cosx, Secx, and an example of odd functions are x3, Sinx, Tanx.
• Periodic Function: The function is considered a periodic function if the same range appears for different domain values and in a sequential manner. The trigonometric functions can be considered periodic functions. For example, the function f(x) = Sinx, have a range [-1, 1] for the different domain values of x = nπ + (-1)nx. Similarly, we can write the domain and the range of the trigonometric functions and prove that the range shows up in a periodic manner.
• Inverse function: The inverse of a function f(x) is denoted by f-1(x). For inverse of a function the domain and range of the given function is changed as the range and domain of the inverse function. The inverse of a function can be prominently seen in algebraic functions and in inverse trigonometric functions. The domain of Sinx is R and its range is [-1, 1], and for Sin-1x the domain is [-1, 1] and the range is R. The inverse of a function exists, if it is a bijective function.
  If a function f(x) = x², then the inverse of the function is f^-1(x) = √x.
• Greatest Integer Function: The greatest integer function is also known as the step function. The greatest integer function rounds up the number to the nearest integer less than or equal to the given number. Clearly, the input variable x can take on any real value. However, the output will always be an integer. Also, all integers will occur in the output set. Thus, the domain of this function is real numbers R, while its range is integers (Z).
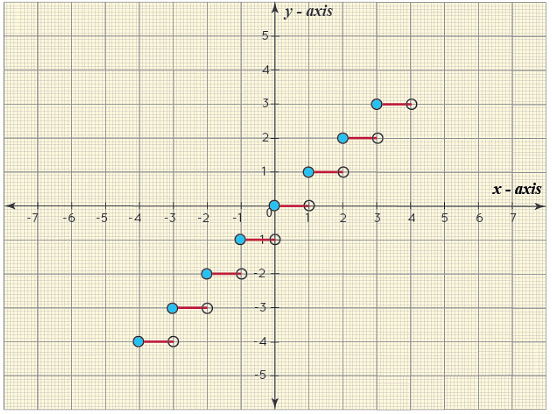  The greatest integer function graph is known as the step curve because of the step structure of the curve.The greatest integral function is denoted as f(x) = ⌊x⌋. For a function taking values from [1, 2), the value of f(x) is 1.
• Composite Function: The composite functions are of the form of gof(x), fog(x), h(g(f(x))), and is made from the individual functions of f(x), g(x), h(x). The composite functions made of two functions have the range of one function forming the domain for another function. Let us consider a composite function fog(x), which is made up of two functions f(x) and g(x).
  Here we write fog(x) = f(g(x)). The range of g(x) forms the domain for the function f(x). It can be considered as a sequence of two functions. If f(x) = 2x + 3 and g(x) = x + 1 we have fog(x) = f(g(x)) = f(x + 1) = 2(x + 1) + 3 = 2x + 5.

4. Types oF Functions - Based on Domain
Functions are used in all the other topics of maths. The functions have been classified based on the types of equations used to define the functions. The function equations generally have algebraic expressions, trigonometric functions, logarithms, exponents, and hence are named based on these domain values. The three broad types of functions based on domain value are as follows.

• Algebraic Function: An algebraic function is helpful to define the various operations of algebra. The algebraic function has a variable, coefficient, constant term, and various arithmetic operators such as addition, subtraction, multiplication, division. An algebraic function is generally of the form of f(x) = aⁿxⁿ + a^{n - 1}x^{n - 1}+ a^n-2x^n-2+ ....... ax + c.
  The algebraic function can also be represented graphically. The algebraic function is also termed as a linear function, quadratic function, cubic function, polynomial function, based on the degree of the algebraic equation.
• Trigonometric Functions: The trigonometric functions also have a domain and range similar to any other function. The six trigonometric functions are f(θ) = sinθ, f(θ) = cosθ, f(θ) = tanθ, f(θ) = secθ, f(θ) = cosecθ. Here the domain value θ is the angle and is in degrees or in radians. These trigonometric functions have been taken based on the ratio of the sides of a right-angle triangle, and are based on the Pythagoras theorem.
  Further from these trigonometric functions, inverse trigonometric functions have also been derived. The domain of the inverse trigonometric function is a real number value and its range is an angle. The trigonometric functions and the inverse trigonometric functions are also sometimes referred to as periodic functions since the principal values are repeated.
• Logarithmic Functions: Logarithmic functions have been derived from the exponential functions. The logarithmic functions are considered as the inverse of exponential functions. Logarithmic functions have a 'log' in the function and it has a base. The logarithmic function is of the form y = log_a x. Here the domain value is the input value of 'x' and is calculated using the Napier logarithmic table. The logarithmic function gives the number of exponential times to which the base has raised to obtain the value of x. The same logarithmic function can be expressed as an exponential function as x = a^y.

Examples on Types of Functions

Example 1: For the given functions f(x) = 3x + 2 and g(x) = 2x - 1, find the value of fog(x).

The given two functions are f(x) = 3x + 2 and g(x) = 2x - 1.
We need to find the function fog(x).
fog(x) = f(g(x))
= f(2x-1)
= 3(2x - 1) + 2
= 6x - 3 + 2
= 6x - 1
Therefore fog(x) = 6x - 1

Example 2: Find the inverse function of the function f(x) = 5x + 4.

The given function is f(x) = 5x + 4
we rewrite it as y = 5x + 4 and simplify it to find the value of x.
y = 5x + 4
y - 4 = 5x
x = (y - 4)/5
f^-1(x) = (x - 4)/5
Therefore the inverse function is f-1(x) = (x - 4)/5