Cheatsheet: Number Series
Introduction
Number series is a common topic in competitive exams, where you are given a sequence of numbers following a specific pattern. The task is to identify the rule and determine the next number in the series, testing your ability to recognize mathematical relationships and patterns.
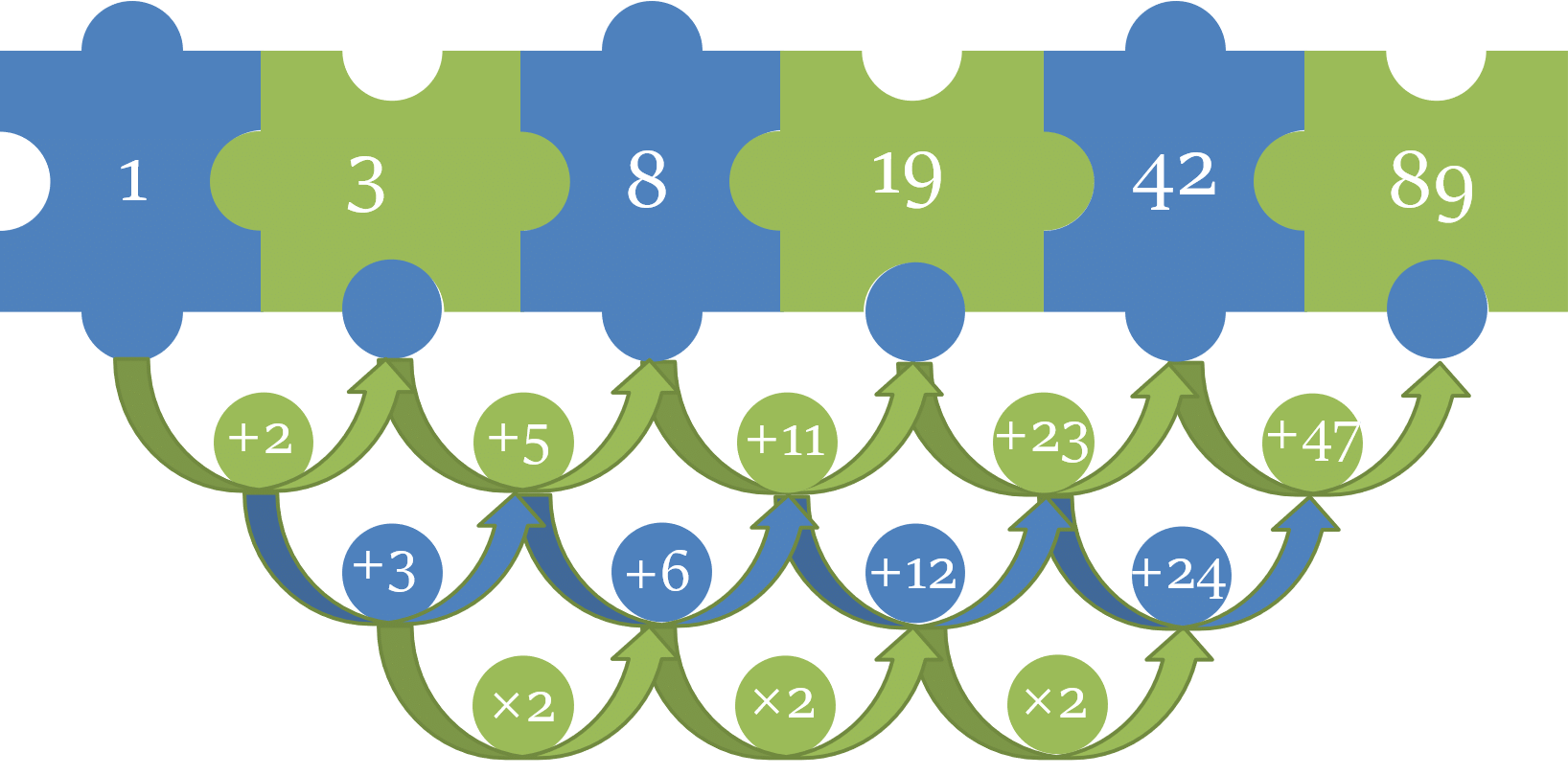
Theory
If the numbers in a series do not follow a simple addition or multiplication pattern, check if you can apply a rule that combines two or more basic arithmetic operations such as addition, subtraction, multiplication, or division. For example, in the series 2, 4, 8, 6, 3,..., the rule is as follows:
Add 2 to the first number to get the second number.
Multiply the second number by 2 to get the third number.
Subtract 2 from the third number to get the fourth number.
Divide the fourth number by 2 to get the fifth number.
This sequence alternates between different operations, showing that not all number series follow one single operation. By identifying the pattern, you can solve such problems more effectively.
Types of Number Series
Arithmetic Progression (AP)
In an arithmetic progression, the difference between any two consecutive terms is constant. This difference is called the common difference (d).
Example: 3, 6, 9, 12, 15 (Here, the common difference is 3).
Geometric Progression (GP)
In a geometric progression, each term is obtained by multiplying the previous term by a constant. This constant is known as the common ratio (r).
Example: 2, 4, 8, 16, 32 (Here, the common ratio is 2).
Harmonic Progression (HP)
A harmonic progression is a sequence where the reciprocals of the terms form an arithmetic progression.
Example: 1, 1/2, 1/3, 1/4, 1/5 (The reciprocals 1, 2, 3, 4, 5 form an arithmetic progression).
Square Series
A series where each term is the square of a number.
Example: 1, 4, 9, 16, 25 (The terms are the squares of 1, 2, 3, 4, 5).
Cube Series
A series where each term is the cube of a number.
Example: 1, 8, 27, 64, 125 (The terms are the cubes of 1, 2, 3, 4, 5).
Fibonacci Series
The Fibonacci series is a sequence in which each term is the sum of the two preceding ones.
Example: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 (Each term is the sum of the two previous terms).
Alternating Series
In an alternating series, the numbers alternate between positive and negative terms, or between two operations.
Example: 2, -4, 8, -16, 32 (The signs of the terms alternate, and the magnitude follows a geometric progression).
Factorial Series
A series formed by factorial numbers, where each term is the factorial of a number.
Example: 1!, 2!, 3!, 4!, 5! (Which is 1, 2, 6, 24, 120).
Tips
Even if the difference between numbers changes (i.e., it is not constant), there can still be a logical rule governing the sequence.
In such cases, examine the differences between consecutive terms. If the differences themselves follow a clear pattern, you can use that information to find the next number in the sequence.
Sometimes, the differences between numbers might form an Arithmetic Progression (AP). For example:
First difference = 1
Second difference = 2
Third difference = 3, and so on.
Look for patterns involving more than one operation, such as alternating between addition and multiplication, or subtraction and division.
Solved Example
32, ?, 1024, 2048, 2048
Try yourself: 9, 5, 6, 10.5, 23 ?
17, 98, 26, ?, 35, 80
Try yourself: 2, 17, 89, 359, 1079, ?
7, 4.5 ,5.5, 12, 49,?
FAQs on Cheatsheet: Number Series
| 1. What are the different types of number series patterns I need to know for IBPS PO? |  |
| 2. How do I find the missing number in a series when the pattern isn't immediately obvious? | |
| 3. Why do I keep getting number series questions wrong even after studying the concepts? | |
| 4. What's the fastest way to solve number series problems under exam time pressure? | |
| 5. Are there any tricks to solving Fibonacci and mixed operation number series quickly? | |
