Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry

Clear all your Class 10 doubts with EduRev Join for Free

Join for Free

Q1. If sec θ + tan θ = 7, then evaluate sec θ – tan θ.

Sol:

We know that,

sec2θ – tan2θ = 1

⇒ (sec θ + tan θ) (sec θ – tan θ) = 1

⇒  (7) (sec θ – tan θ) = 1 …[sec θ + tan θ = 7]

∴ sec θ – tan θ = 1/7

Q2. Prove that
(1+tan A - sec A) (1+tan A + sec A) = 2 tan A

Sol:

LHS = (1+tan A)² - sec² A

= 1+ tan2 A + 2 tan A - sec² A

= sec² A + 2 tan A - sec² A

= 2 tan A = RHS

Q3. If tan A = cot B, then find the value of (A+B)

Sol:

We have,

tan A = cot B

tan A = tan(90°-B)

A = 90° - B

Thus, A + B = 90°

Q4. If sinθ + sin2θ = 1 then prove that cos²θ + cos⁴θ = 1.

Sol:

sinθ + sin²θ = 1

⇒ sinθ + (1-cos²θ) = 1

⇒ sinθ - cos²θ = 0

⇒ sinθ = cos²θ

Squaring both sides, we get

sin²θ = cos⁴θ

⇒ 1 - cos²θ = cos⁴θ

⇒ cos⁴θ + cos²θ = 1

Q5. If tan θ + cot θ = 5, find the value of tan²θ + cotθ.

Sol:

tan θ + cot θ = 5 …[Given]

⇒ tan²θ + cot²θ + 2 tan θ cot θ = 25 …[Squaring both sides]

⇒ tan²θ + cot²θ + 2 = 25

∴ tan²θ + cot²θ = 23

6. If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A.

Sol:

sec 2A = cosec (A – 27°)

⇒ cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)]

⇒ 90° – 2A = A – 27°

⇒ 90° + 27° = 2A + A

⇒ 3A = 117°

∴ ∠A = 117°/3 = 39°

Q7. Evaluate: sin² 19° + sin²71°.

Sol:

sin²19° + sin²71°

= sin²19° + sin² (90° – 19°) …[∵ sin(90° – θ) = cos θ]

= sin² 19° + cos² 19° = 1 …[∵ sin² θ + cos² θ = 1]

Q8. In a triangle ABC, write cos(B+C/2) in terms of angle A.

Sol:

In a triangle,

A+B+C = 180°

B+C = 180° - A

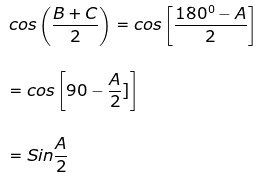
Q9. If secθ sinθ = 0, then find the value of θ.

Sol:

We have,

secθ sinθ = 0

Thus θ = 0

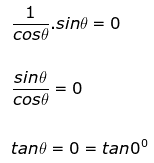
Q10. Find the value of sin²41° + sin²49°

Sol:

sin²41° + sin²49°

= sin²(90°-49°) + sin²49°

= cos²49° + sin²49°

= 1

Q11. If tan A = cot B, prove that A + B = 90°.

Sol:

tan A = cot B

∴ tan A = tan (90° − B)

⇒ A = 90° − B

⇒ A + B = 90°

Q12. Express sin 67° + cos 75° in terms of ratios of angles between 0° and 45°.
Sol:

∵ 67° = 90° − 23° and 75° = 90° − 15° 

∴ sin 67° + cos 75°

= sin (90° − 23°) + cos (90° − 15°)

= cos 23° + sin 15°

Q13. What is the value of sinθ. cos(90° - θ) + cosθ . sin(90° - θ)?

Sol:

sinθ ·cos(90° − θ) + cosθ · sin(90° − θ)

= sinθ · sinθ + cosθ · cosθ [∵ cos(90° − θ) = sinθ , sin(90° − θ) = cos θ]

= sin² θ + cos² θ

= 1

Q14. If tan θ = cot (30° + θ ), find the value of θ .

Sol:

We have,

tan θ = cot (30° + θ)

= tan [90° − (30° + θ)]

= tan [90° − 30° − θ]

= tan (60° − θ)

⇒ θ = 60° − θ

⇒ θ + θ = 60°

⇒ 2θ = 60°

⇒ θ = 60°/2

⇒ θ = 30°

Q15. If sin 3θ = cos (θ - 6)° and 3θ and (θ - 6)° are acute angles, find the value of θ.

Sol:

We have,

sin3θ = cos(θ − 6)° = sin[90°−(θ − 6)°] ∵ [sin (90° − θ) = cos θ]

⇒ 3θ = 90° − (θ − 6)°

⇒ 3θ = 90° − θ + 6°

⇒ 3θ + θ = 96°

⇒ 4θ = 96°/4

⇒ θ = 24°

Q16. Show that: tan 10° tan 15° tan 75° tan 80° = 1

Sol:

We have,

L.H.S. = tan 10° tan 15° tan 75° tan 80°

= tan (90° − 80°) tan 15° tan (90° − 15°) tan 80°

= cot 80° tan 15 cot 15° tan 80°

= (cot 80° × tan 80°) × (tan 15° × cot 15°)

= 1× 1

= 1 = R.H.S.

Introduction to Trigonometry Class 10 Maths Important Questions Short Answer-I (2 Marks)

17. If tan 2A = cot (A - 18°), where 2A is an acute angle, find the value of A.

Sol:

tan 2A = cot (A - 18°)

⇒ cot (90° - 2A) = cot (A - 18°) [∵ cot (90° -0) - tan θ]

⇒ 90° - 2A = A - 18°

⇒ 3A = 108°

⇒ A = 108°/3

⇒ A = 36°