Mixture and Alligation: Shortcuts & Tricks | Quantitative Techniques for CLAT PDF Download
Basic Definition
- Mixture: It is the process of mixing two or more elements/ingredients together.
- Allegation: It is a process or a rule that tells us how to mix two or more ingredients/mixtures to get the desired mixture of a certain price & concentration.
Now there are 2 ways of applying the allegation technique to questions.
Formula Method
Quantity of cheaper/ Quantity of dearer = (Price of dearer – Mean price)/ (Mean Price- Price of cheaper)
Diagram Method
The above-mentioned formula can be better understood using the diagram method & it is more convenient to use this method.
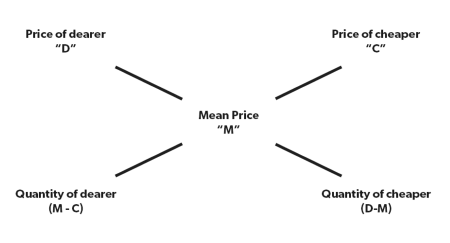
Note 1: Please note that allegation is a concept with the help of which we can find the mean price if 2 or more ingredients are mixed in some ratio or we can also find the ratio in which two or more items should be mixed to get a certain price or concentration of the mixture.
Note 2: (D-M)/(M-C) is nothing but the ratio of quantities of both the items, so even if we are given a ratio in which 2 items are mixed, we can find the “M”.
Now let’s try to solve a variety of problems using the allegation method which will help you in understanding the concept in a much better way.
Examples
Q1: If 20 kgs of rice which cost 45 Rs/Kg is mixed with 25 kgs of rice which costs 30 Rs/Kg. What will be the price of the final mixture?
Sol: In this question, we have to find “M”
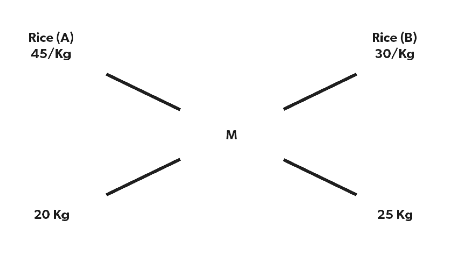 Now as we know, (45-M)/(M-30)=25/20
Now as we know, (45-M)/(M-30)=25/20
⇒ (45-M)/(M-30)= 5/4
⇒180-4M = 5M- 150
⇒ 330= 9M
⇒ M= 330/9= 36.6 Rs/Kg
Q2: Oranges of type A that cost 60 Rs/Kg is mixed with the orange of type B that costs 80 Rs/Kg in a ratio of 3:5. What will be the price of the resultant mixture of oranges?
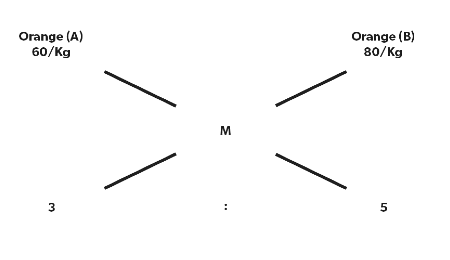 Sol: Again applying the same formula,
Sol: Again applying the same formula,
(60-M)/(M-80)= 5/3
180-3M = 5M-400
580= 8M
M= 580/8= 72.5 Rs
Q3: If rice or 45 Rs/kg is mixed with rice of 35 Rs/kg and the price of the resultant mixture is 42.5 Rs/kg. What is the ratio that they were mixed in?
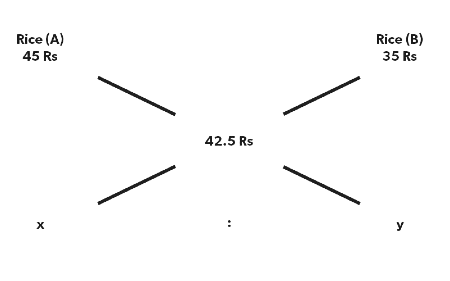 Sol: As we know, (45-42.5)/(42.5-35) = Y/X
Sol: As we know, (45-42.5)/(42.5-35) = Y/X
2.5/7.5= Y/X
1/3 = Y/X, hence they were mixed in the ratio of 3:1.
Q4: Mixture A which contains 30% water is mixed with Mixture B which has 20% water in a ratio of 2:5. What will be the % of water in the resultant mixture?
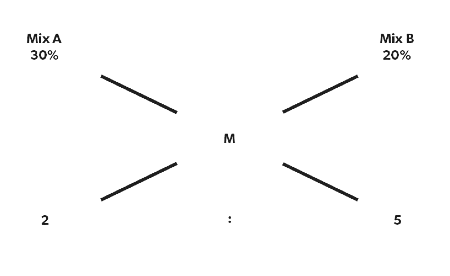
Sol: Allegation can also be applied to percentages & not just absolute values.
(30%-M)/(M-20%)= 5/2
60% – 2M= 5M – 100%
160% = 7M
M = 160%/7 = 22.8%
Q5: A shopkeeper sells one item at 20% profit and another item at 5% profit. If the overall profit of the shopkeeper is 10 per cent. What is the ratio of the CP of item A to item B?
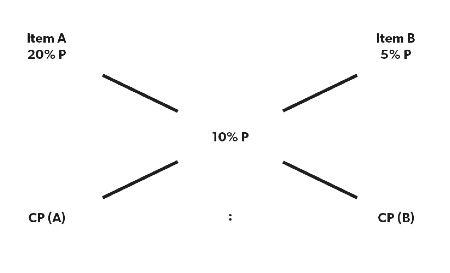
Sol: Here, the ratio of quantities will give us ratio of the cost price
So, (20%-10%)/ (10%-5%)= CP (B)/CP (A)
10%/5%= CP (B)/ CP (A)
2:1 = CP (A)/ CP(B)
|
49 videos|155 docs|73 tests
|
FAQs on Mixture and Alligation: Shortcuts & Tricks - Quantitative Techniques for CLAT
| 1. What is the basic definition of mixture and alligation? |  |
| 2. What are some shortcuts and tricks for solving mixture and alligation problems quickly? |  |
| 3. How can mixture and alligation problems be solved using the concept of ratios? |  |
| 4. What is the rule of weighted averages and how is it applied in mixture and alligation problems? |  |
| 5. How does the method of false position help in solving mixture and alligation problems? |  |
















