Simplification: Shortcuts & Tricks | Quantitative Techniques for CLAT PDF Download
Given below are some of the tips and tricks to solve Simplification.
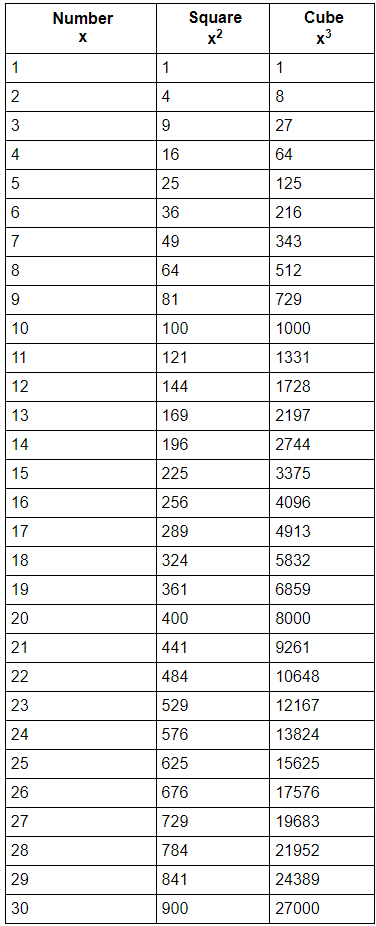
- Learn the basics firsts to ace this topic, it includes Tables, square, Fractional Value.
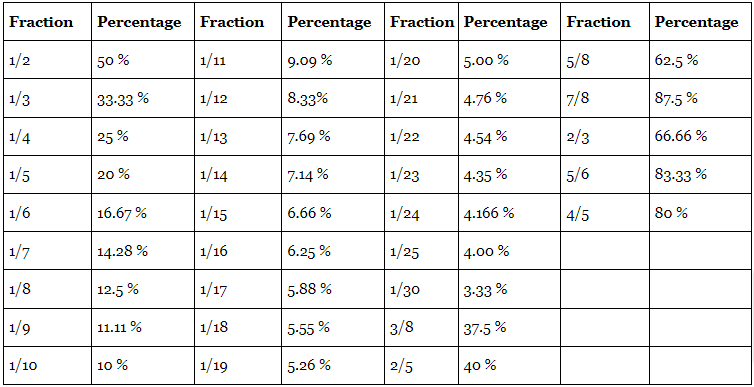
Some Other Important things you must remember is the fractional values:
- Learn the different divisibility rules as it will help you to fasten your speed. Some of them are given below:

- Learn the BODMAS rule where, BODMAS stands for:
- Brackets
- Orders
- Division
- Multiplication
- Addition
- Subtraction
This rule implies that the bracket must be open first and then the first operation that needs to be done is of Division moving onto Multiplication, Addition and Subtraction.
- Solve at least 20 simplification questions in daily basis so that you get a great grasp on this topic.
- As the saying goes that there is no substitute of practice , it is actually true in this topic. The more your practice, the better you will be able to understand this concept and at times, are able to find the correlation in some calculations, can observe a pattern and might develop a few tips and tricks on his own to solve that particular question.
Examples
Q1: 0.03 × 0.01 – 0.003 ÷ 100 + 0.03 =?
(a) 0.03027
(b) 0.0327
(c) 0.3027
(d) 1.03027
(e) 0.003027
Ans: e
Sol:
? = 0.0003 – 0.00003 + 0.03
= 0.03027
Q2: 25×3.25+50.4÷24 = ?
(a) 84.50
(b) 83.35
(c) 83.53
(d) 82.45
(e) 92.84
Ans: c
Sol:
? = 81.25+2.1
= 83.35
Q3: 350% of ? ÷50+248=591
(a) 4900
(b) 4890
(c) 4850
(d) 4950
(e) 4750
Ans: a
Sol:
350 × ?/100 × 1/50 = 343
? = 4900
Q4: 1/2 of 3842+15% of ? =2449
(a) 3520
(b) 3250
(c) 3350
(d) 3540
(e) 2850
Ans: a
Sol:
1/2×3842+15/100× ?=2449
? =(528×100)/15
? =3520
Q5: (833.25-384.45)÷24= ?
(a) 1.87
(b) 20.1
(c) 2.01
(d) 18.7
(e) 16.7
Ans: a
Sol:
?=448.8/24
?=18.7
|
49 videos|155 docs|73 tests
|
FAQs on Simplification: Shortcuts & Tricks - Quantitative Techniques for CLAT
| 1. What are some popular shortcuts and tricks for simplification in mathematics? |  |
| 2. How can I simplify algebraic expressions using the distributive property? |  |
| 3. What is the concept of combining like terms and how can it simplify mathematical expressions? |  |
| 4. How can I simplify expressions by canceling out common factors? |  |
| 5. Can exponent rules be used to simplify expressions? If so, how? |  |




















