Important Derivations: Newton's Laws of Motion | Physics for JEE Main & Advanced PDF Download
Derivation of First Law of Motion from Newton’s Second Law
To derive the First Law of Motion (Law of Inertia) from Newton’s Second Law of Motion (F = ma), we consider a particle that is at rest or moving with a constant velocity (zero acceleration). The First Law of Motion states that an object remains at rest or moves with a constant velocity unless acted upon by an external force.
Let’s assume the following:
– F = Net external force acting on the particle (resultant force)
– m = Mass of the particle
– a = Acceleration of the particle
According to Newton’s Second Law of Motion, we have: Now, for the First Law of Motion, we want to consider the case when the particle is at rest or moving with a constant velocity. This means the acceleration (a) is zero. In other words, the net external force acting on the particle is also zero.
Now, for the First Law of Motion, we want to consider the case when the particle is at rest or moving with a constant velocity. This means the acceleration (a) is zero. In other words, the net external force acting on the particle is also zero.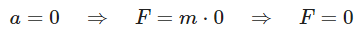 This implies that if the net external force acting on the particle is zero (F=0), the acceleration of the particle (a) is also zero. Therefore, the particle will either be at rest or move with a constant velocity.
This implies that if the net external force acting on the particle is zero (F=0), the acceleration of the particle (a) is also zero. Therefore, the particle will either be at rest or move with a constant velocity.
Hence, we have derived the First Law of Motion (Law of Inertia) from Newton’s Second Law of Motion, which states that an object remains at rest or moves with a constant velocity unless acted upon by an external force.
Law of Conservation of Momentum Derivation
The law of conservation of momentum is one of the most prominent laws in physics. The conservation of momentum law principle tells us that the total momentum of a system is always conserved for an isolated system. Let us learn more about the conservation of momentum along with derivation and solved problems.
Momentum Conservation Principle
Law of conservation of momentum states that
For two or more bodies in an isolated system acting upon each other, their total momentum remains constant unless an external force is applied. Therefore, momentum can neither be created nor destroyed.
The principle of conservation of momentum is a direct consequence of Newton’s third law of motion.
Derivation of Conservation of Momentum
Consider two colliding particles A and B whose masses are m1 and m2 with initial and final velocities as u1 and v1 of A and u2 and v2 of B. The time of contact between two particles is given as t.
A=m1(v1−u1)
(change in momentum of particle A)
B=m2(v2−u2)
(change in momentum of particle B)
FBA=−FAB
(from third law of motion)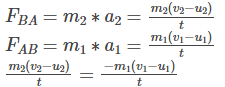
m1u1 + m2u2 = m1v1 + m2v2
Therefore, above is the equation of law of conservation of momentum where
m1u1 + m2u2
is the representation of total momentum of particles A and B before the collision and
m1v1 + m2v2
is the representation of total momentum of particles A and B after the collision.
Examples of Law of Conservation of Momentum
Following are the examples of law of conservation of momentum:
- Air-filled balloons
- System of gun and bullet
- Motion of rockets
Solved Problems on Law of Conservation of Momentum
Q1. There are cars with masses 4 kg and 10 kg respectively that are at rest. The car having the mass 10 kg moves towards the east with a velocity of 5 m.s-1. Find the velocity of the car with mass 4 kg with respect to ground.
Ans: Given,
m1 = 4 kg
m2 = 10 kg
v1 = ?
v2 = 5 m.s-1
Pinitial = 0, as the cars are at rest
Pfinal = p1 + p2
Pfinal = m1.v1 + m2.v2
= (4 kg).(v1) + (10 kg).(5 m.s-1)
We know from the law of conservation of momentum that,
Pinitial = Pfinal
0=4 kg.v1+50 kg.m.s-1
v1 = 12.5 m.s-1
Q2. Find the velocity of a bullet of mass 5 grams which is fired from a pistol of mass 1.5 kg. The recoil velocity of the pistol is 1.5 m.s-1.
Ans: Given,
Mass of bullet, m1 = 5 gram = 0.005 kg
Mass of pistol, m2 = 1.5 kg
The velocity of a bullet, v1 = ?
Recoil velocity of pistol, v2 = 1.5 m.s-1
Using law of conservation of momentum,
m1u1 + m2u2 = m1v1 + m2v2
Here, Initial velocity of the bullet, u1 = 0
Initial recoil velocity of a pistol, u2 = 0
∴ (0.005 kg)(0) + (1.5 kg)(0) = (0.005 kg)(v1) + (1.5 kg)(1.5 m.s-1)
0 = (0.005 kg)(v1)+(2.25 kg.m.s-1)
v1=-450 m.s-1
Hence, the recoil velocity of the pistol is 450 m.s-1.
Derivation of Centripetal Acceleration
Centripetal acceleration is the rate of change of tangential velocity. The net force causing the centripetal acceleration of an object in a circular motion is defined as centripetal force. The derivation of centripetal acceleration is very important for students who want to learn the concept in-depth. The direction of the centripetal force is towards the centre, which is perpendicular to the velocity of the body.
The centripetal acceleration derivation will help students to retain the concept for a longer period of time. The derivation of centripetal acceleration is given in a detailed manner so that students can understand the topic with ease.
The centripetal force keeps a body constantly moving with the same velocity in a curved path. The mathematical explanation of centripetal acceleration was first provided by Christian Huygens in the year 1659. The derivation of centripetal acceleration is provided below.
Centripetal Acceleration Derivation
The force of a moving object can be written as
F = ma ........... (1)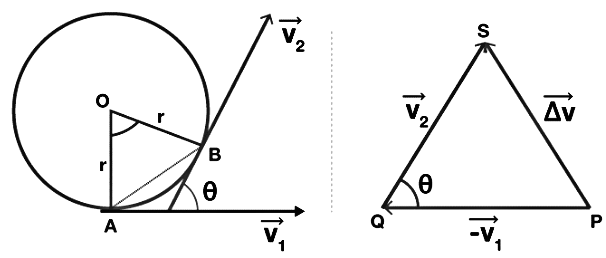
From the diagram given above, we can say that,
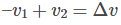
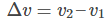
The triangle PQS and AOB are similar. Therefore,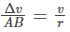
AB = arc AB = vΔt
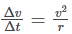
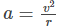
|
268 videos|740 docs|171 tests
|
FAQs on Important Derivations: Newton's Laws of Motion - Physics for JEE Main & Advanced
| 1. What is the derivation of the First Law of Motion from Newton's Second Law? |  |
| 2. What are Newton's Laws of Motion? |  |
| 3. How is the First Law of Motion related to inertia? |  |
| 4. Can the First Law of Motion be applied to everyday situations? |  |
| 5. What are some practical applications of Newton's Laws of Motion? |  |
















