CAT Exam > CAT Notes > Logical Reasoning (LR) and Data Interpretation (DI) > Important Formulas: Venn Diagrams & Set Theory
Important Formulas: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Set Theory
A set is a group of objects. Each object is known as a member of the set. A set can be represented using curly brackets. So a set containing the numbers 2, 4, 6, 8, 10, ... is: {2, 4, 6, 8, 10, ... } . Sets are often also represented by letters, so this set might be E = {2, 4, 6, 8, 10, ...} . Alternatively, E = {even numbers} .
Common Sets
Some sets are commonly used and so have special notation:
for example: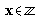
means that x is in the set of integers,
i.e x is a integer
ϵ means ' is a member of '
Other Notation
Subsets
- If A is a subset of B, then all of the elements of A are also in B. For example, if A = {1, 2, 3} and B = {1, 2, 3, 4, 5} then A Í B (Í means is a subset of).
Number of Members
- If A = {1, 2, 4, 8}, then n(A) = 4. This is because n(A) means the number of members in set A.
The Universal Set
- The universal set is the set of all sets. All sets are therefore subsets of the universal set.
Venn Diagrams
- Venn diagrams are used to represent sets. Here, the set A{1, 2, 4, 8} is shown using a circle. In Venn diagrams, sets are usually represented using circles. The universal set is the rectangle. The set A is a subset of the universal set and so it is within the rectangle.

- The complement of A, written A', contains all events in the sample space which are not members of A. A and A' together cover every possible eventuality.

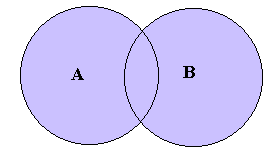
- A ÈB means the union of sets A and B and contains all of the elements of both A and B. This can be represented on a Venn Diagram as follows:
 AÇB means the intersection of sets A and B. This contains all of the elements which are in both A and B. AÇB is shown on the Venn Diagram below:
AÇB means the intersection of sets A and B. This contains all of the elements which are in both A and B. AÇB is shown on the Venn Diagram below: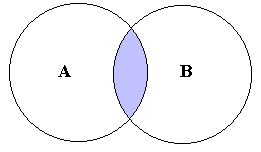
- An important result connecting the number of members in sets and their unions and intersections is:
n(A) + n(B) - n(AÇB) = n(AÈB)
The document Important Formulas: Venn Diagrams & Set Theory | Logical Reasoning (LR) and Data Interpretation (DI) - CAT is a part of the CAT Course Logical Reasoning (LR) and Data Interpretation (DI).
All you need of CAT at this link: CAT
|
77 videos|180 docs|96 tests
|
FAQs on Important Formulas: Venn Diagrams & Set Theory - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are Venn diagrams and how are they used in set theory? |  |
Ans. Venn diagrams are visual representations used in set theory to illustrate the relationships between sets. They consist of overlapping circles or ovals, with each circle representing a set and the overlap representing the elements that are common to both sets.
| 2. How can Venn diagrams help in solving set theory problems in competitive exams? |  |
Ans. Venn diagrams provide a visual and intuitive way to solve set theory problems in competitive exams. By representing sets and their relationships through overlapping circles, they allow us to easily determine the intersection, union, and complement of sets, making it easier to solve complex problems efficiently.
| 3. What are the main components of a Venn diagram? |  |
Ans. The main components of a Venn diagram include circles or ovals representing sets, labeled regions within the circles to represent specific elements or subsets, and overlapping regions to represent the intersection of sets.
| 4. How can one determine the complement of a set using a Venn diagram? |  |
Ans. To determine the complement of a set using a Venn diagram, we need to represent the universal set (the set that contains all possible elements) and the set we are interested in. The complement of a set is then represented by the region outside the set's circle or oval, but within the universal set.
| 5. Can Venn diagrams be used to solve problems involving more than two sets in set theory? |  |
Ans. Yes, Venn diagrams can be used to solve problems involving more than two sets in set theory. In such cases, multiple circles or ovals are used, with overlapping regions representing the intersections between the sets. By carefully analyzing the overlapping regions, we can determine the relationships and solve complex problems efficiently.
Related Searches





















