Practice Questions: Simple Interest and Compound Interest | Quantitative Techniques for CLAT PDF Download
Q1: The difference in simple interest and compound interest on a certain sum of money in 2 years at 10 % p.a. is Rs. 50. The sum is
(a) Rs. 10000
(b) Rs. 6000
(c) Rs. 5000
(d) Rs. 2000
Ans: c
If Diff. between SI & CI for 2 years is Rs. x, then Principal = x (100/r)2 P = 50 x (100x100)/(10x10) → P = 5000.
Q2: The difference in simple interest and compound interest on a certain sum of money in 2 years at 18 % p.a. is Rs. 162. The sum is
(a) Rs. 4000
(b) Rs. 5200
(c) Rs. 4250
(d) Rs. 5000
Ans: d
If Diff. between SI & CI for 2 years is Rs. x, Principal = x (100/r)2 P = 162 x (100x100)/(18x18) → P = 5000.
Q3: The compound interest on a certain sum of money for 2 years is Rs. 208 and the simple interest for the same time at the same rate is Rs. 200. Find the rate %.
(a) 5 %
(b) 6 %
(c) 7 %
(d) 8 %
Ans: d
SI = Rs. 200 = Rs. 100 + Rs. 100
CI = Rs. 208 = Rs. 100 + Rs. 108 (In first year SI & CI are equal.)
Therefore, Rs.8 Gap is because of the interest of 1st year interest.
Rs. 8 is interest on Rs. 100, R= (8x100)/(100x1) % ,R = 8%
Q4: The difference between compound interest and simple interest on a certain sum for 2 years at 10 % is Rs. 25. The sum is
(a) Rs. 1200
(b) Rs. 2500
(c) Rs. 750
(d) Rs. 1250
Ans: b
Apply: Principal = x (100/r)2 where x is the difference in CI & SI for 2 years.
∴ P = 25(100/10)2 = 2500.
Q5: The simple interest on a certain sum for 3 years in Rs. 225 and the compound interest on the same sum for 2 years is Rs. 165. Find the rate percent per annum.
(a) 20 %
(b) 2.5 %
(c) 5 %
(d) 15 %
Ans: a
SI for 3 years = 225 → SI for 1 year = 75
∴ CI for 1 year = 75. So CI for 2nd year = 90 and SI for 2nd year = 75. Difference = 15
∴ Rate of interest = (15/75)x100 = 20 %
Q6: The simple interest on a sum of money for 2 years is Rs. 150 and the compound interest on the same sum at same rate for 2 years is Rs. 155. The rate % p.a. is
(a) 16 %
(b) 20/3 %
(c) 12 %
(d) 10 %
Ans: b
SI for 3 years = 150 → SI for 1 years = 75
∴ CI for 1 year = 75. So CI for 2nd year = 80 and SI for 2nd year = 75. Difference = 5
∴ Rate of interest = (5/75) x 100 = 20/3 %.
Q7: Mihir’s capital is 5/4 times more than Tulsi’s capital. Tulsi invested her capital at 50 % per annum for 3 years (compounded annually). At what rate % p.a. simple interest should Mihir invest his capital so that after 3 years, they both have the same amount of capital?
(a) 20/3 %
(b) 10 %
(c) 50/3 %
(d) 1.728 %
Ans: c
Let, the capital of Tulsi = 4.
∴ Capital of Mihir = 9.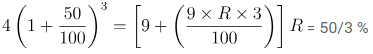
Q8: The difference in simple interest and compound interest on a certain sum of money in 3 years at 10 % p.a. is Rs. 372. The sum is
(a) Rs. 8000
(b) Rs.9000
(c) Rs. 10000
(d) Rs. 12000
Ans: d
Let us assume P= Rs. 1000. SI= Rs. 300, CI = Rs. 331
Difference = 331 - 300 = Rs. 31.
Applying the unitary method, the difference Rs. 372 is 12 times Rs. 31.
Therefore, the principle will also be 12 times of Rs. 1000 i.e. Rs. 12000.
Q9: Sahil’s capital is 1/6 times more than Chaya’s capital. Chaya invested her capital at 20 % per annum for 2 years (compounded annually). At what rate % p.a. simple interest should Sahil invest his capital so that after 2 years, they both have the same amount of capital?
(a) 10%
(b) 11 5/7%
(c) 20%
(d) 13 5/7%
Ans: b
Let, the capital of Sahil = 6. ∴ Capital of Chaya = 7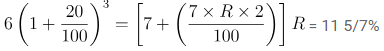
Q10: The difference in simple interest and compound interest on a certain sum of money in 3 years at 20 % p.a. is Rs. 640. The sum is
(a) Rs. 5000
(b) Rs. 8500
(c) Rs. 8250
(d) Rs. 6000
Ans: a
Let us assume P= Rs. 1000, SI = Rs. 600, CI = Rs. 728
Difference= 728 – 600 = Rs. 128
Applying the unitary method, the difference Rs. 640 is 5 times Rs. 128.
Therefore, the principle will also be 5 times of Rs. 1000 i.e. Rs. 5000.
|
57 videos|108 docs|73 tests
|






















