JEE Advanced Previous Year Questions (2018 - 2024): Complex Numbers | Mathematics (Maths) for JEE Main & Advanced PDF Download
2024
Q1: Let S = {a + b√2 : a, b ∈ ℤ},
T₁ = {(-1 + √2)ⁿ : n ∈ ℕ},
T₂ = {(1 + √2)ⁿ : n ∈ ℕ}.
Then which of the following statements is (are) TRUE? [JEE Advanced 2024 Paper 1]
(a) ℤ ∪ T₁ ∪ T₂ ⊂ S
(b) T₁ ∩ (0, 1/2024) = ϕ, where ϕ denotes the empty set.
(c) T₂ ∩ (2024, ∞) ≠ ϕ
(d) For any given a, b ∈ ℤ, cos(π(a + b√2)) + i sin(π(a + b√2)) ∈ ℤ if and only if b = 0, where i = √-1.
Ans: (a), (c), (d)
(A) (-1 + √2)ⁿ = m + √2n, m, n ∈ ℤ
(1 + √2)ⁿ = m₁ + √2n₁, m₁, n₁ ∈ ℤ
⇒ ℤ ∪ T₁ ∪ T₂ ⊆ S
but b√2 ∈ S for negative b ∈ ℤ.
So ℤ ∪ T₁ ∪ T₂ ⊂ S
(B) (√2 - 1)ⁿ = 1 / (√2 + 1)ⁿ < 1/2024
⇒ 2024 < (√2 + 1)ⁿ, ∃n ∈ ℕ
⇒ T₁ ∩ (0, 1/2024) ≠ ϕ
(C) (1 + √2)ⁿ > 2024, ∃n ∈ ℕ
⇒ T₂ ∩ (2024, ∞) ≠ ϕ
(D) sin(π(a + b√2)) = 0 ⇒ b = 0, a ∈ ℤ.
⇒ Options (A), (C), (D) are Correct.
Q2: Let f(x) = x⁴ + ax³ + bx² + c be a polynomial with real coefficients such that f(1) = -9. Suppose that i√3 is a root of the equation 4x³ + 3ax² + 2bx = 0, where i = √-1. If α₁, α₂, α₃, and α₄ are all the roots of the equation f(x) = 0, then |α₁|² + |α₂|² + |α₃|² + |α₄|² is equal to ________. [JEE Advanced 2024 Paper 1]
Ans: 20
f(1) = 1 + a + b + c = -9 ⇒ a + b + c = -10 .... (i)
4x³ + 3ax² + 2bx = 0 roots are √3i, -√3i, 0
⇒ 4x² + 3ax + 2b = 0 < √3i, -√3i
⇒ a = 0 & (2b/4) = (√3i)(-√3i)
b = 6 use a, b in (i) ⇒ c = -16
⇒ f(x) = x⁴ + 6x² - 16 = 0
(x² + 8)(x² - 2) = 0
⇒ x = ±√8i, ±√2
⇒ |α₁|² + |α₂|² + |α₃|² + |α₄|² = 20
2023
Q1: Let 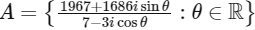 . If A contains exactly one positive integer n, then the value of n is [JEE Advanced 2023 Paper 1]
. If A contains exactly one positive integer n, then the value of n is [JEE Advanced 2023 Paper 1]
Ans: 281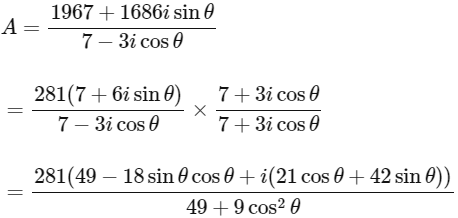
For positive integer
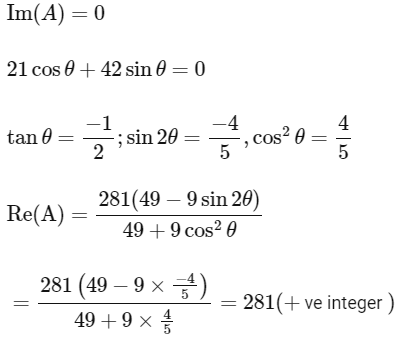
Q2: Let z be a complex number satisfying  , where
, where  denotes the complex conjugate of z. Let the imaginary part of z be nonzero.
denotes the complex conjugate of z. Let the imaginary part of z be nonzero.
Match each entry in List-I to the correct entries in List-II. 
(a) (P)→(1)(Q)→(3)(R)→(5)(S)→(4)
(b) (P)→(2)(Q)→(1)(R)→(3)(S)→(5)
(c) (P)→(2)(Q)→(4)(R)→(5)(S)→(1)
(d) (P)→(2)(Q)→(3)(R)→(5)(S)→(4) [JEE Advanced 2023 Paper 1]
Ans: (b)
Take conjugate both sides
Let 
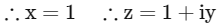
Put in (1)
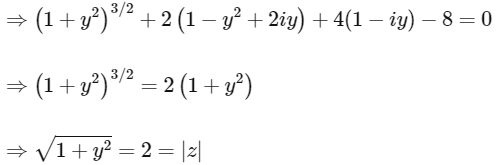
Also 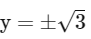
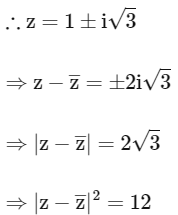
Now 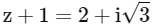
|z + 1|2 = 4 + 3 = 7
∴ (P)→(2)(Q)→(1)(R)→(3)(S)→(5)
∴ Option (b) is correct.
2022
Q1: Let z be a complex number with a non-zero imaginary part. If 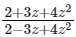 is a real number, then the value of |z|2 is _________. [JEE Advanced 2022 Paper 1]
is a real number, then the value of |z|2 is _________. [JEE Advanced 2022 Paper 1]
Ans: 0.49 to 0.51
For a complex number z = x + iy, it's conjugate 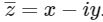 . Now z is purely real when y = 0.
. Now z is purely real when y = 0.
When y = 0 then z = x + i × (0) = x and 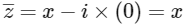
∴ 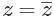 when z is purely real.
when z is purely real.
Now given, 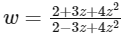 is real
is real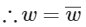
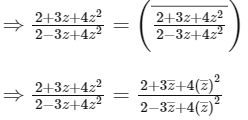
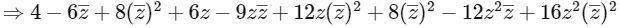
= 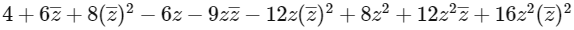

y = 0 not possible as given z is a complex number with non-zero imaginary part.
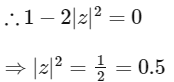
Q2: Let 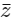 denote the complex conjugate of a complex number z and let
denote the complex conjugate of a complex number z and let 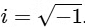 . In the set of complex numbers, the number of distinct roots of the equation
. In the set of complex numbers, the number of distinct roots of the equation 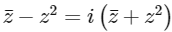 is _________. [JEE Advanced 2022 Paper 1]
is _________. [JEE Advanced 2022 Paper 1]
Ans: 4
Let z = x + iy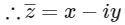
Given, 
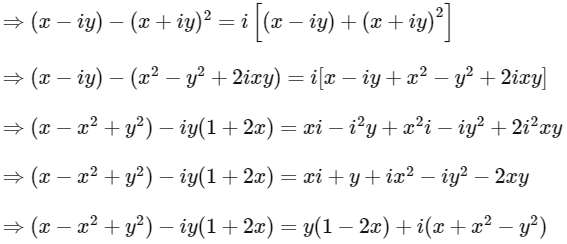
Comparing both sides real part we get,
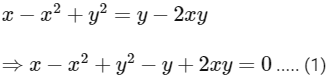
And comparing both sides imaginary part we get,
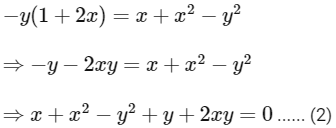
Adding equation (1) and (2) we get,

Case 1 : When x = 0 :
Put x = 0 at equation (1), we get
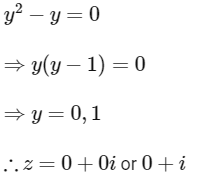
Case 2 : When y = −1/2 :
Put y = −1/2 in equation (1), we get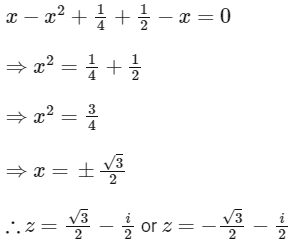
∴ Number of distinct z = 4
Q3: Let 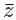 denote the complex conjugate of a complex number z. If z is a non-zero complex number for which both real and imaginary parts of
denote the complex conjugate of a complex number z. If z is a non-zero complex number for which both real and imaginary parts of 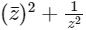 are integers, then which of the following is/are possible value(s) of |z| ?
are integers, then which of the following is/are possible value(s) of |z| ?
(a) 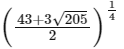
(b) 
(c) 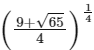
(d) 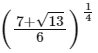 [JEE Advanced 2022 Paper 2]
[JEE Advanced 2022 Paper 2]
Ans: (a)
Let, complex number 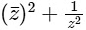 is a new complex number ω.
is a new complex number ω.
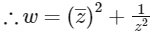
Now, Let 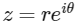 where r = |z| and θ = argument
where r = |z| and θ = argument
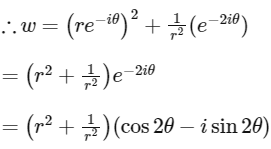
∴ Real part of 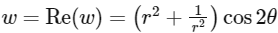
Imaginary part of 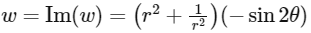
Given both Re(ω) and Im(ω) are integer.
∴ Let Re(ω) = I1
and Im(ω) = I2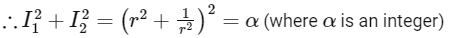
Now, 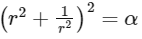
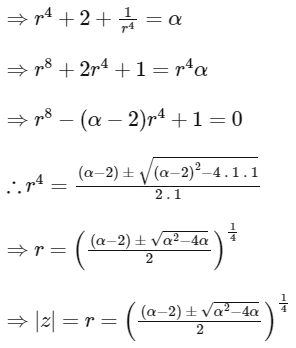
In option only positive sign is given so ignoring negative sign we get,
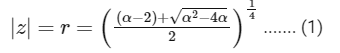
From option (A),
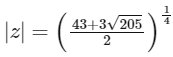
Comparing with (1), we get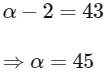
Putting α = 45 in (1), we get
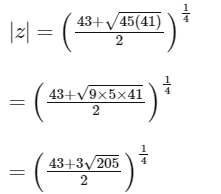
∴ Option (A) is correct.
We can re-write
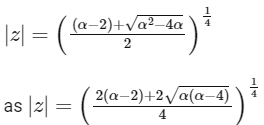
Comparing with option (B) we get,
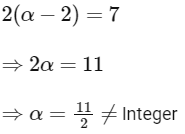
Option (B) is incorrect.
Similarly option (C) and (D) also incorrect.
2021
Q1: Let θ1, θ2, ........, θ10 = 2π. Define the complex numbers z1 = eiθ1, zk = zk − 1eiθk for k = 2, 3, ......., 10, where i = √−1. Consider the statements P and Q given below :
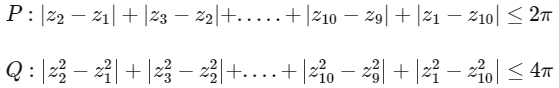
Then,
(a) P is TRUE and Q is FALSE
(b) Q is TRUE and P is FALSE
(c) both P and Q are TRUE
(d) both P and Q are FALSE [JEE Advanced 2021 Paper 1]
Ans: (c)
Both P and Q are true.
∵ Length of direct distance ≤ length of arc
i.e. | z2 − z1 | = length of line AB ≤ length of arc AB.
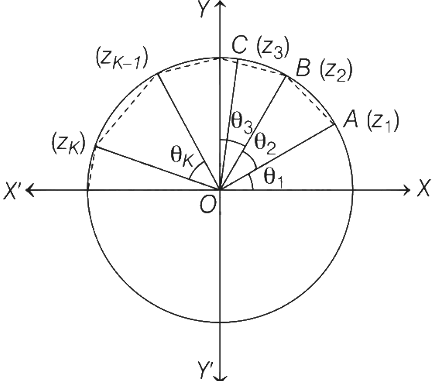
| z3 − z2 | = length of line BC ≤ length of arc BC.
∴ Sum of length of these 10 lines ≤ sum of length of arcs (i.e. 2π) (because θ1 + θ2 + θ3 + .... + θ10 = 2π (given)
∴ | z2 − z1 | + | z3 − z2 | + ..... + | z1 − z10 | ≤ 2π → P is true.
And | zk2 − zk−12 | = | zk − zk − 1 | | zk + zk − 1 |
As we know that,
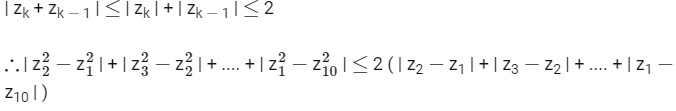
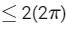
≤ 4π → Q is true.
Q2: For any complex number w = c + id, let arg(ω)∈(−π, π], where i = √−1. Let α and β be real numbers such that for all complex numbers z = x + iy satisfying 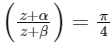 , the ordered pair (x, y) lies on the circle x2 + y2 + 5x − 3y + 4 = 0, Then which of the following statements is (are) TRUE?
, the ordered pair (x, y) lies on the circle x2 + y2 + 5x − 3y + 4 = 0, Then which of the following statements is (are) TRUE?
(a) α = −1
(b) αβ = 4
(c) αβ = −4
(d) β = 4 [JEE Advanced 2021 Paper 1]
Ans: (d)
Circle x2 + y2 + 5x − 3y + 4 = 0 cuts the real axis (X-axis) at (−4, 0), (−1, 0).
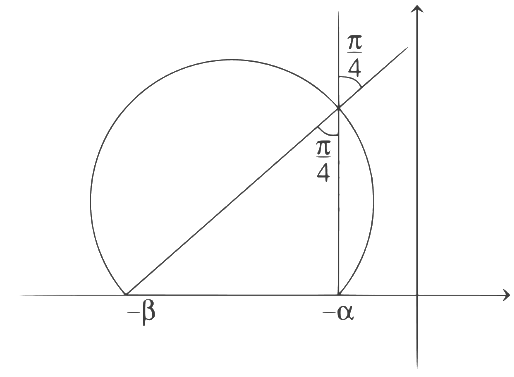
 implies z is on arc and (− α, 0) and (− β, 0) subtend π/4 on z.
implies z is on arc and (− α, 0) and (− β, 0) subtend π/4 on z.
So, α = 1 and β = 4
Hence, αβ = 1 × 4 = 4 and β = 4
2020
Q1: For a complex number z, let Re(z) denote that real part of z. Let S be the set of all complex numbers z satisfying 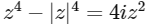 , where i = √−1. Then the minimum possible value of |z1 − z2|2, where z1, z2∈S with Re(z1) > 0 and Re(z2) < 0 is _____ [JEE Advanced 2020 Paper 2]
, where i = √−1. Then the minimum possible value of |z1 − z2|2, where z1, z2∈S with Re(z1) > 0 and Re(z2) < 0 is _____ [JEE Advanced 2020 Paper 2]
Ans: 8
For a complex number z, it is given that,
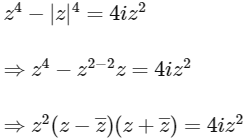
So, either 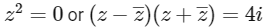
Now, Case - I, if z2=0 and z = x + iy
So, x2 - y2 + 2ixy = 0
⇒ x2 - y2 = 0
and xy = 0
⇒ x = y = 0
⇒ z = 0 which is not possible according to given conditions.
Case - II, if 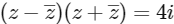 and
and
z = x + iy
So, 
⇒ xy = 1 is an equation of rectangular hyperbola and for minimum value of |z1 − z2|2, the z1 and z2 must be vertices of the rectangular hyperbola.
Therefore, z1 = 1 + i and z2 = -1 - i
∴ Minimum value of |z1 − z2|2
= (1 + 1)2 + (1 + 1)2
= 4 + 4
= 8
Q2: Let S be the set of all complex numbers z satisfying |z2 + z + 1| = 1. Then which of the following statements is/are TRUE?
(a) |z + 1/2| ≤ 1/2 for all z ∈ S
(b) |z| ≤ 2 for all z ∈ S
(c) |z + 1/2| ≥ 1/2 for all z ∈ S
(d) The set S has exactly four elements [JEE Advanced 2020 Paper 1]
Ans: (b) & (c)
It is given that the complex number satisfying
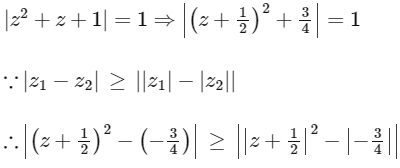
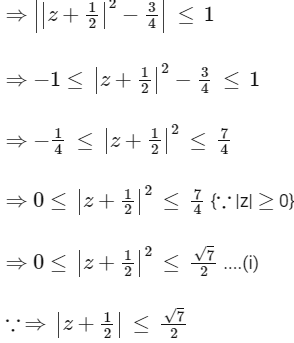
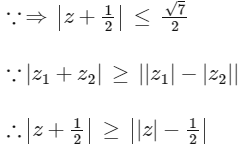
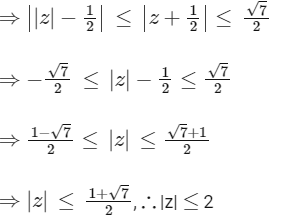
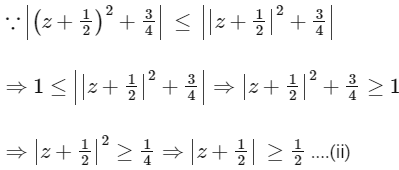
from Eqs. (i) and (ii), we get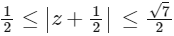
 |
Download the notes
JEE Advanced Previous Year Questions (2018 - 2024): Complex Numbers
|
Download as PDF |
2019
Q1: Let ω ≠ 1 be a cube root of unity. Then the maximum of the set 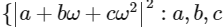 distinct non-zero integers} equals _____ [JEE Advanced 2019 Paper 1]
distinct non-zero integers} equals _____ [JEE Advanced 2019 Paper 1]
Ans: 3
Given, ω ≠ 1 be a cube root of unity, then 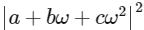
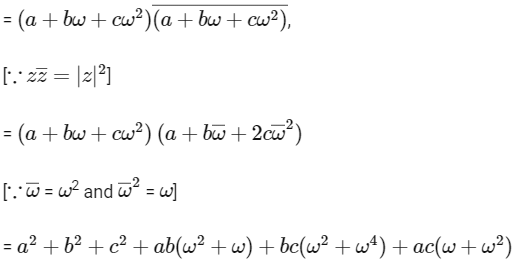
[as ω3 = 1)
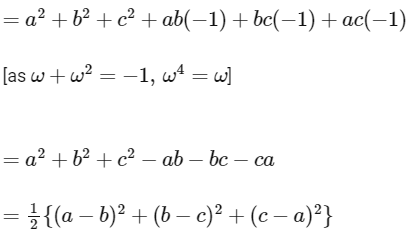
∵ a, b and c are distinct non-zero integers. For minimum value a= 1, b = 2 and c = 3
∴ 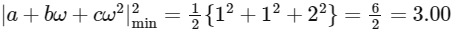
Q2: Let S be the set of all complex numbers z satisfying 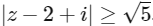 . If the complex number z0 is such that
. If the complex number z0 is such that 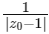 is the maximum of the set
is the maximum of the set 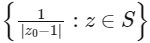 , then the principal argument of
, then the principal argument of 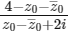 is
is
(a) π / 4
(b) 3π / 4
(c) - π / 2
(d) π / 2 [JEE Advanced 2019 Paper 1]
Ans: (c)
The complex number z satisfying 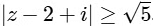 , which represents the region outside the circle (including the circumference) having centre (2, −1) and radius √5 units.
, which represents the region outside the circle (including the circumference) having centre (2, −1) and radius √5 units.
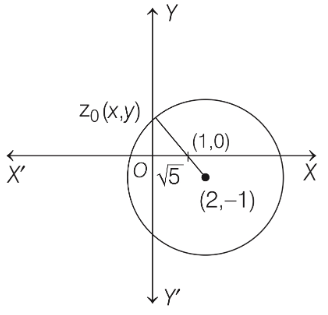
Now, for 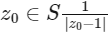 is maximum.
is maximum.
When |z0 − 1| is minimum. And for this it is required that z0 ∈ S, such that z0 is collinear with the points (2, −1) and (1, 0) and lies on the circumference of the circle |z − 2 + i| = √5.
So let z0 = x + iy, and from the figure 0 < x < 1 and y >0.
So, 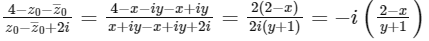
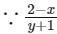 is a positive real number, so
is a positive real number, so 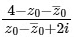 is purely negative imaginary number.
is purely negative imaginary number.
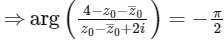
2018
Q1: Let s, t, r be non-zero complex numbers and L be the set of solutions 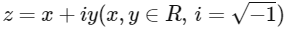 of the equation
of the equation 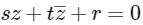 where
where 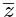 = x − iy. Then, which of the following statement(s) is(are) TRUE? [JEE Advanced 2018 Paper 2]
= x − iy. Then, which of the following statement(s) is(are) TRUE? [JEE Advanced 2018 Paper 2]
(a) If L has exactly one element, then |s| ≠ |t|
(b) If |s| = |t|, then L has infinitely many elements
(c) The number of elements in L ∩ {z:|z − 1 + i|=5} is at most 2
(d) If L has more than one element, then L has infinitely many elements [JEE Advanced 2018 Paper 2]
Ans: (a), (c) & (d)
We have,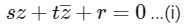
On taking conjugate,
On solving Eqs. (i) and (ii), we get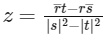
(a) For unique solutions of z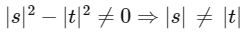 It is true
It is true
(b) If |s| = |t|, then 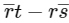 may or may not be zero. So, z may have no solutions.∴ L may be an empty set.
may or may not be zero. So, z may have no solutions.∴ L may be an empty set.
It is false.
(c) If elements of set L represents line, then this line and given circle intersect at maximum two point. Hence, it is true.
(d) In this case locus of z is a line, so L has infinite elements. Hence, it is true.
|
209 videos|447 docs|187 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Complex Numbers - Mathematics (Maths) for JEE Main & Advanced
| 1. What are complex numbers and why are they important in JEE Advanced? |  |
| 2. How do you represent complex numbers on the Argand plane? |  |
| 3. What are the basics of operations involving complex numbers that are essential for JEE Advanced? |  |
| 4. What is the significance of the modulus and argument of a complex number in JEE Advanced? |  |
| 5. How can De Moivre's Theorem be applied in solving complex number problems in JEE Advanced? |  |