JEE Advanced Previous Year Questions (2018 - 2024): Definite Integrals and Applications of Integrals | Mathematics (Maths) for JEE Main & Advanced PDF Download
2024
Q1: Let f: [0, π2] → [0,1] be the function defined by f(x) = sin²x and let g: [0, π2] → [0, ∞) be the function defined by 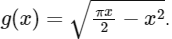
The Value of 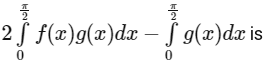 __________. [JEE Advanced 2024 Paper 2]
__________. [JEE Advanced 2024 Paper 2]
Ans: 0
apply kings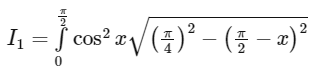
add both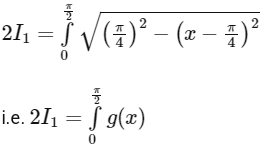
Now, 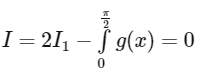
Q2: Let f: [0, π2] → [0,1] be the function defined by f(x) = sin²x and let g: [0, π2] → [0, ∞) be the function defined by 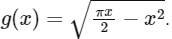
The value of 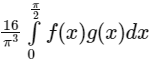 is ________. [JEE Advanced 2024 Paper 2]
is ________. [JEE Advanced 2024 Paper 2]
Ans: 0.25
Now, 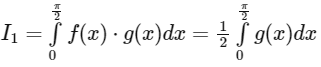
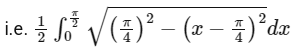
Using 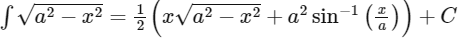
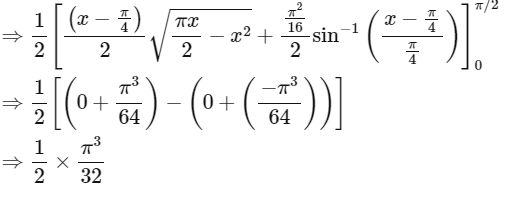
Now 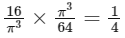
= 0.25
Q3: Let the function f : [1, ∞) → ℝ be defined by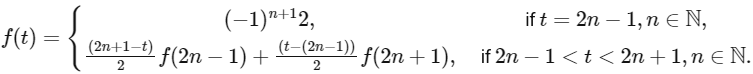
Define 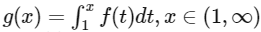 . Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8) and
. Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8) and 
Then the value of α + β is ______. [JEE Advanced 2024 Paper 2]
Ans: 5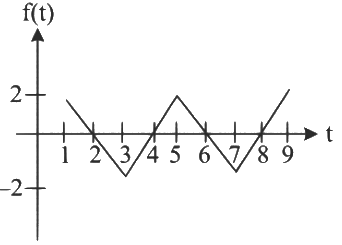

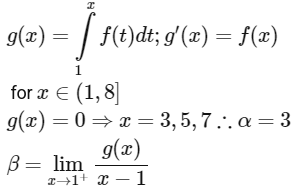
Apply L'pital
= g'(1⁺)1 = f(1⁺)
β = 2
∴ α + β = 5
Q4: Set S = {(x, y) ∈ ℝ × ℝ : x ≥ 0, y ≥ 0, y² ≤ 4x, y² ≤ 12 - 2x and 3y +√8x ≤ 5 √8}. If the area of the region S is α √2 , then α is equal to:
(a) 172
(b) 173
(c) 174
(d) 175 [JEE Advanced 2024 Paper 2 ]
Ans: (b)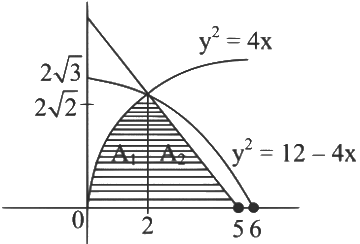 Point of intersection of all curves is (2, 2 √2).
Point of intersection of all curves is (2, 2 √2).
Area = A₁ + A₂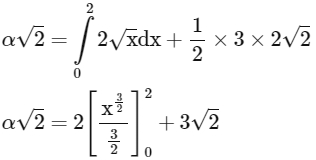
α √2 = 17√23
α = 173
2023
Q1: For x ∈ R, let
 . Then the minimum value of the function f : R →R defined by
. Then the minimum value of the function f : R →R defined by 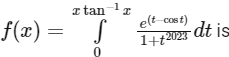 is : [JEE Advanced 2023 Paper 2]
is : [JEE Advanced 2023 Paper 2]Ans: 0
Q2: Let n ≥ 2 be a natural number and f : [0, 1] → R be the function defined by
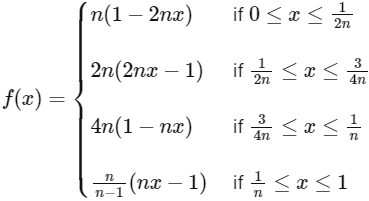
If n is such that the area of the region bounded by the curves x = 0, x = 1, y = 0 and y = f(x) is 4 , then the maximum value of the function f is : [JEE Advanced 2023 Paper 1]
Ans: 8
f(x) is decreasing in 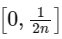
increasing in 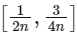
decreasing in 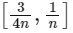
increasing in 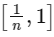
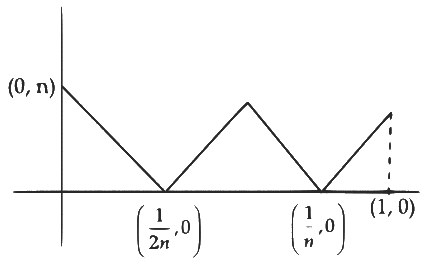
Area = 
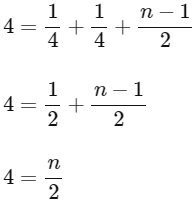
n = 8
Q2: Let f :(0, 1)→ R be the function defined as 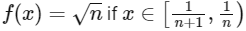 where n ∈ N. Let g:(0, 1) → R be a function such that
where n ∈ N. Let g:(0, 1) → R be a function such that 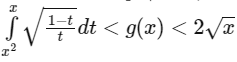 for all x ∈ (0, 1). Then
for all x ∈ (0, 1). Then 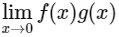
(a) does NOT exist
(b) is equal to 1
(c) is equal to 2
(d) is equal to 3 [JEE Advanced 2023 Paper 1]
Ans: (c)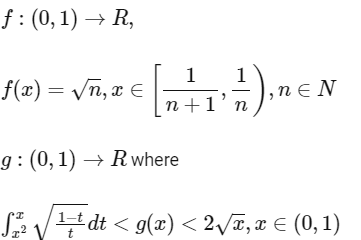
Now (According to the question)
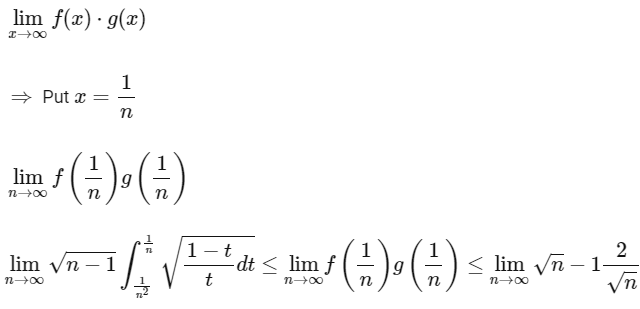
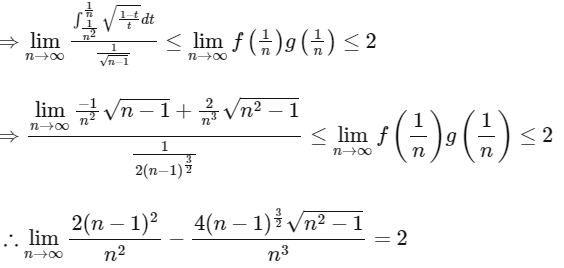
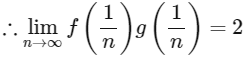 (Using Sandwich Theorem)
(Using Sandwich Theorem)
2022
Q1: The greatest integer less than or equal to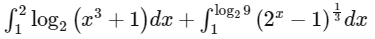 is ___________. [JEE Advanced 2022 Paper 2]
is ___________. [JEE Advanced 2022 Paper 2]
Ans: 5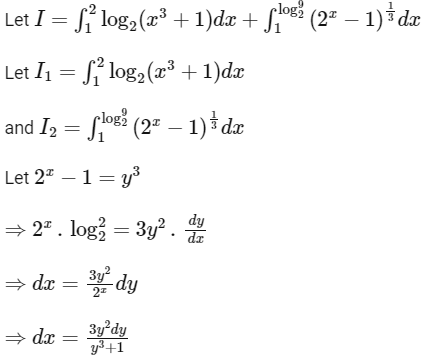
When, 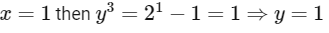
When, 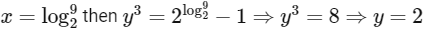
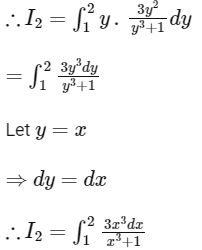
Now, 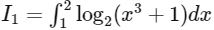
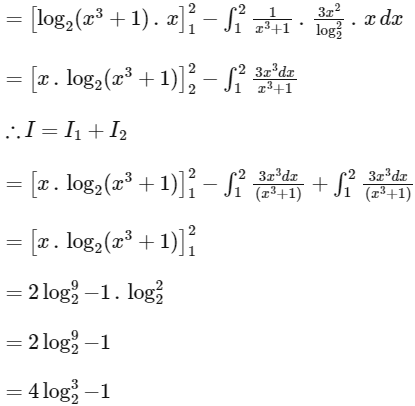
= 4 x 1.58 - 1
= 6.32 - 1
= 5.32
Greatest integer value fo
I = [5.32] = 5
Q2: Consider the functions f, g : R → R defined by
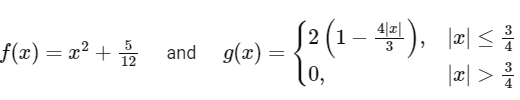
If α is the area of the region 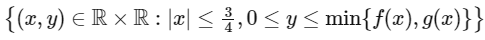 , then the value of 9α is: [JEE Advanced 2022 Paper 2]
, then the value of 9α is: [JEE Advanced 2022 Paper 2]
Ans: 6
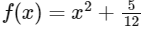
This represent upward parabola.
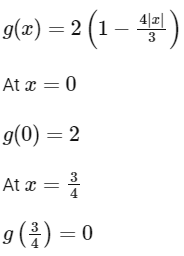
∴ Graph is

Intersection point of f(x) and g(x) at first quadrant,
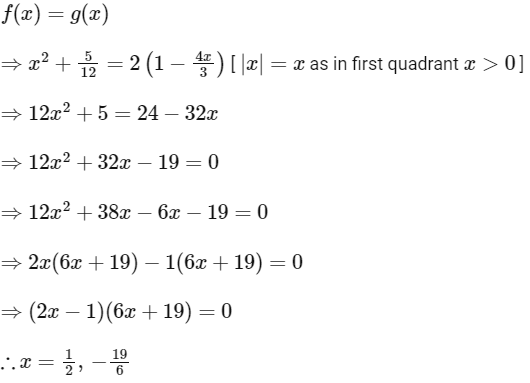
In first quadrant x = 1/2
When, x = 1/2
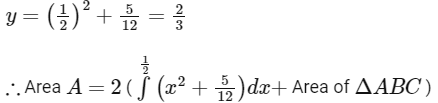
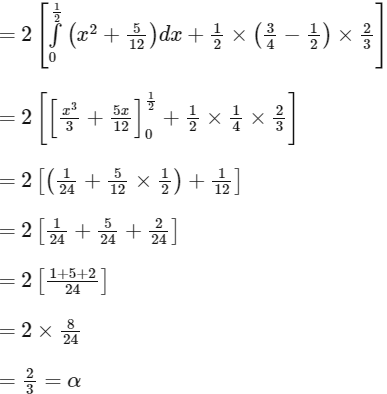
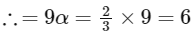
2021
Q1: Let f1 : (0, ∞) → R and f2 : (0, ∞) → R be defined by
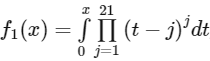 , x > 0 and
, x > 0 and 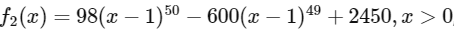 , where, for any positive integer n and real numbers a1, a2, ....., an,
, where, for any positive integer n and real numbers a1, a2, ....., an, 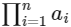 denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, ∞).
denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, ∞).
The value of 2m1 + 3n1+ m1n1 is ___________. [JEE Advanced 2021 Paper 2]
Ans: 57.00
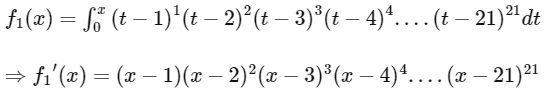
From sign scheme of f1'(x), we observe that f(x) has local minima at x = 4k + 1, k∈W i.e. f1'(x) changes sign from −ve to + ve which are x = 1, 5, 9, 13, 17, 21 and f(x) has local maxima at x = 4k + 3, k ∈ W i.e. f1'(x) changes sign from + ve to − ve, which are x = 3, 7, 11, 15, 19.
So, m1 = number of local minima points = 6
and n1 = number of local maxima points = 5
Hence, 2m1 + 3n1 + m1n1
= 2 × 6 + 3 × 5 + 6 × 5
= 57
Q2: Let f1 : (0, ∞) → R and f2 : (0, ∞) → R be defined by 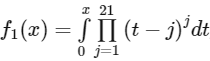 , x > 0 and
, x > 0 and 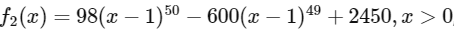 , where, for any positive integer n and real numbers a1, a2, ....., an,
, where, for any positive integer n and real numbers a1, a2, ....., an, 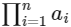 denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, ∞).
denotes the product of a1, a2, ....., an. Let mi and ni, respectively, denote the number of points of local minima and the number of points of local maxima of function fi, i = 1, 2 in the interval (0, ∞).
The value of 6m2 + 4n2+ 8m2n2 is ___________. [JEE Advanced 2021 Paper 2]
Ans: 6.00
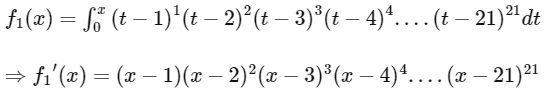
From sign scheme of f1'(x), we observe that f(x) has local minima at x = 4k + 1, k∈W i.e. f1'(x) changes sign from −ve to + ve which are x = 1, 5, 9, 13, 17, 21 and f(x) has local maxima at x = 4k + 3, k ∈ W i.e. f1'(x) changes sign from + ve to − ve, which are x = 3, 7, 11, 15, 19.
So, m1 = number of local minima points = 6
and n1 = number of local maxima points = 5
Hence, 2m1 + 3n1 + m1n1
= 2 × 6 + 3 × 5 + 6 × 5
= 57
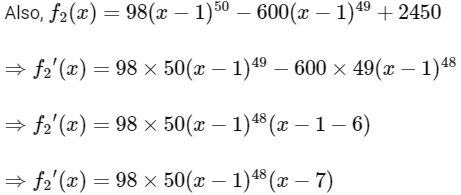

Clearly, m2 = 1 and n2 = 0
So, 6m2 + 4n2+ 8m2n2
= 6 + 0 + 0
= 6
Q3: Let 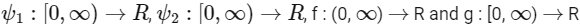 be functions such that f(0) = g(0) = 0,
be functions such that f(0) = g(0) = 0,
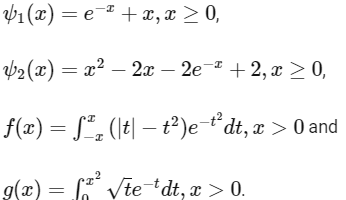
Which of the following statements is TRUE?
(a) 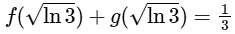
(b) For every x > 1, there exists an α ∈ (1, x) such that 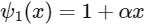
(c) For every x > 0, there exists a β ∈ (0, x) such that 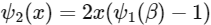
(d) f is an increasing function on the interval (0, 3/2) [JEE Advanced 2021 Paper 2]
Ans: (c)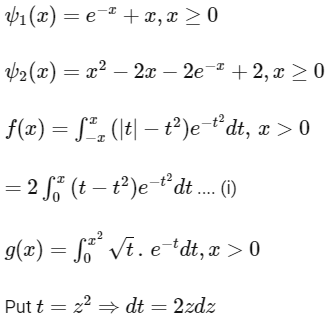
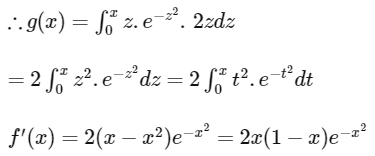
∴ f is increasing for x∈(0, 1) and f is decreasing for x ∈ (1, ∞). Hence, option (d) is incorrect.
Now,
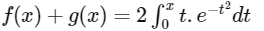
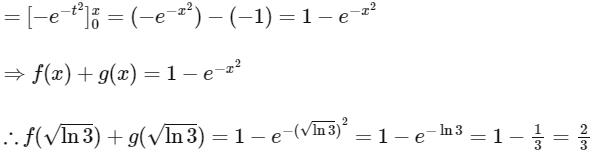
Hence, option (a) is incorrect.
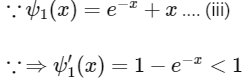
Now, 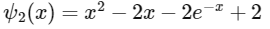
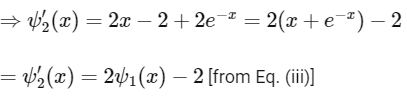
By LMVT,
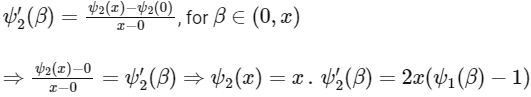
Hence, option (c) is correct.
Q4: Let  and
and 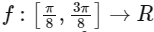 be functions such that
be functions such that 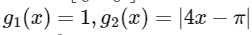 and f(x)=sin2x, for all
and f(x)=sin2x, for all 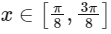 . Define
. Define 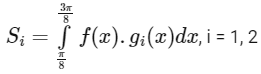
The value of 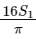 is _____________. [JEE Advanced 2021 Paper 2]
is _____________. [JEE Advanced 2021 Paper 2]
Ans: 2.00
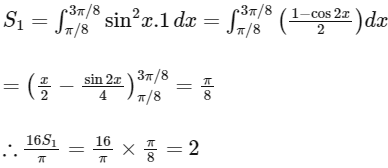
Q5: Let 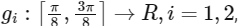 and
and 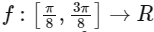 be functions such that
be functions such that 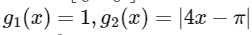 and f(x)=sin2x, for all
and f(x)=sin2x, for all 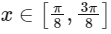 . Define
. Define 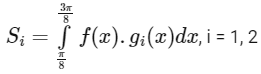
The value of 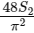 is _____________. [JEE Advanced 2021 Paper 2]
is _____________. [JEE Advanced 2021 Paper 2]
Ans: 1.50
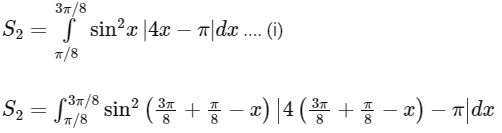
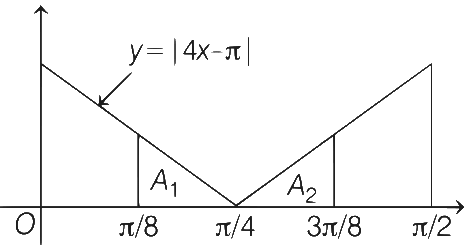
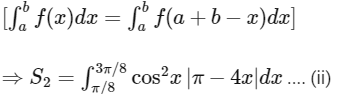
Adding Eqs. (i) and (ii), we get
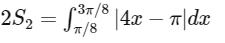
From figure,
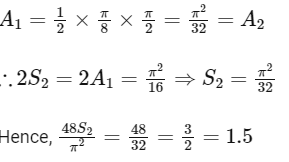
Q6: The area of the region
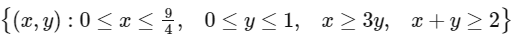 is
is
(a) 11/32
(b) 35/96
(c) 37/96
(d) 13/32 [JEE Advanced 2021 Paper 1]
Ans: (a)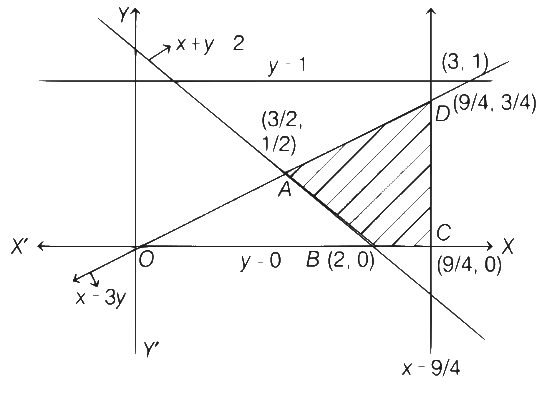
Required area = Shaded region
On solving x + y = 2 and x = 3y, we get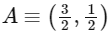
On solving y = 0 and x + y = 2, we get
B ≡ (2, 0)
On solving x = 9/4 and x = 3y, we get
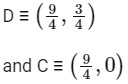
Required area = Area of ∆OCD − Area of ∆OBA
2020
Q1: Let f : R → R be a differentiable function such that its derivative f' is continuous and f(�) = −6. If F : [0, π] → R is defined by 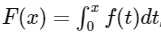 , and if
, and if 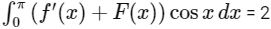 , then the value of f(0) is ______ [JEE Advanced 2020 Paper 2]
, then the value of f(0) is ______ [JEE Advanced 2020 Paper 2]
Ans: 4
It is given that, for functions
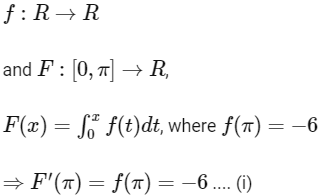
Now, 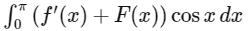
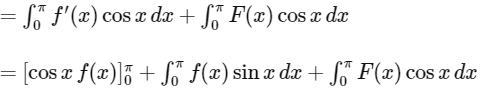
{by integration by parts}
= 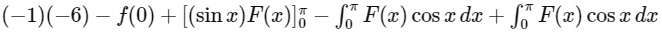
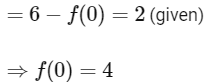
Q2: Let the functions f : R → R and g : R → R be defined by
f(x) = ex − 1 − e−|x − 1|
and g(x) = 1/2(ex − 1 + e1 − x).
The the area of the region in the first quadrant bounded by the curves y = f(x), y = g(x) and x = 0 is
(a) 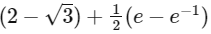
(b) 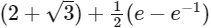
(c) 
(d) 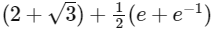 [JEE Advanced 2020 Paper 1]
[JEE Advanced 2020 Paper 1]
Ans: (a)
The given functions f : R → R and g : R → R be defined by
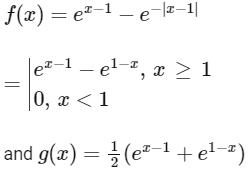
For point of intersection of curves f(x) and g(x) put f(x) = g(x)
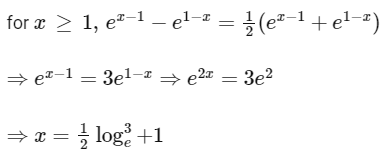
So, required area is
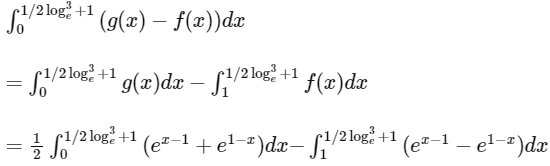
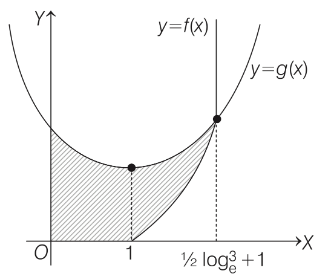
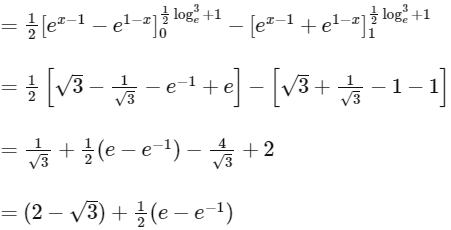
 |
Download the notes
JEE Advanced Previous Year Questions (2018 - 2024): Definite Integrals and Applications of Integrals
|
Download as PDF |
2019
Q1: The value of the integral
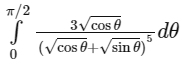 equals ______. [JEE Advanced 2019 Paper 2]
equals ______. [JEE Advanced 2019 Paper 2]Ans: 0.5
The given integral
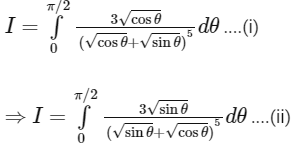
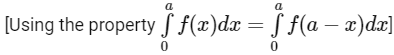
Now, on adding integrals (i) and (ii), we get
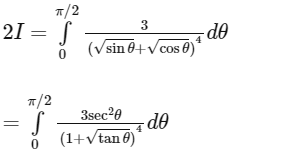
Now, 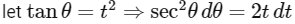
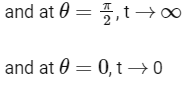
So, 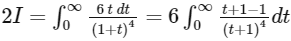
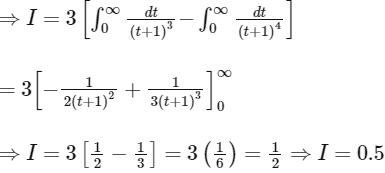
Q2: If 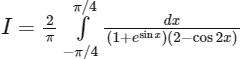 , then 27I2 equals .______ [JEE Advanced 2019 Paper 1]
, then 27I2 equals .______ [JEE Advanced 2019 Paper 1]
Ans: 4
Given,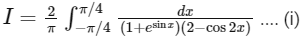
On applying property
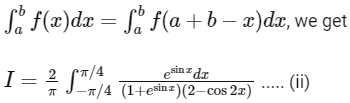
On adding integrals (i) and (ii), we get

Put, 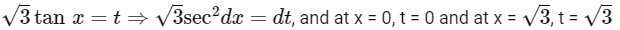
So, 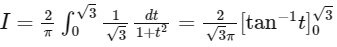
= 
Q3: The area of the region {(x, y) : xy ≤ 8, 1 ≤ y ≤ x2} is
(a) 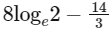
(b) 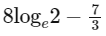
(c) 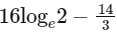
(d) 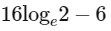 [JEE Advanced 2019 Paper 1]
[JEE Advanced 2019 Paper 1]
Ans: (c)
The given region
{(x, y) : xy ≤ 8, 1 ≤ y ≤ x2}.
From the figure, region A and B satisfy the given region, but only A is bounded region, so area of bounded region
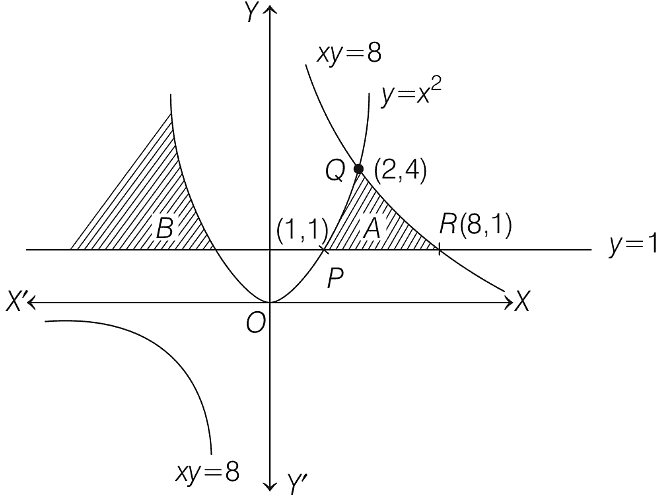
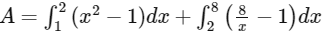
[∴ Points P(1, 1), Q(2, 4) and R(8, 1)]
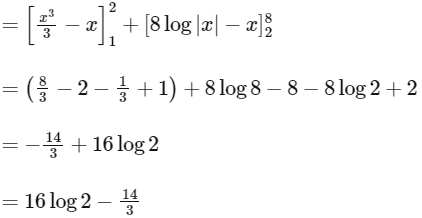
2018
Q1: The value of the integral
 is ______. [JEE Advanced 2018 Paper 2]
is ______. [JEE Advanced 2018 Paper 2]
Ans: 2
Let, 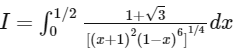
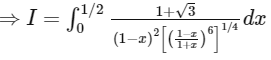
Put, 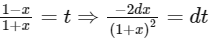
When, 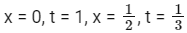

|
209 videos|447 docs|187 tests
|






















