Quant Practice Questions for ACT - 3 | Mathematics for ACT PDF Download
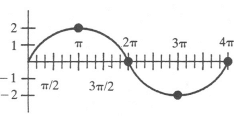
Q1: Draw the graph of y = 2 sin 1/2 x.
 View Answer
View AnswerAns:
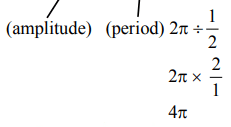
Q2: Find the value of sin(30° + 45°)
 View Answer
View AnswerAns: Expand the formula:
sin(30° + 45°) = sin 30° cos 45° + cos 30° sin 45°
Substitute values:
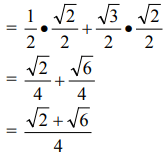
The cosine of the sum of two angles equals the product of their cosines minus the product of their sines. Memorize: cos(α + β) = cos α cos β – sin α sin β
Q3: Simplify cos A tan A, when cos A ≠ 0.
 View Answer
View AnswerAns:
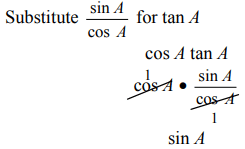
Q4: Simplify tan2 θ cos2 θ csc θ.
 View Answer
View AnswerAns:
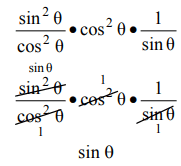
Q5: A kite has 80 meters of string out. The string makes an angle of 30° with the ground. How far above the ground is the kite?

 View Answer
View AnswerAns:
Q6: Evaluate sin 45° • cos 60°
 View Answer
View AnswerAns: Substitute the trigonometric function values:
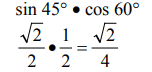
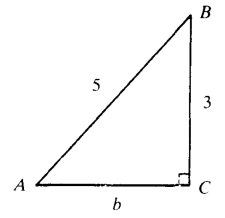
Q7: If ∠A is an acute angle and sin A = 3/5 , find tan A.
 View Answer
View AnswerAns:
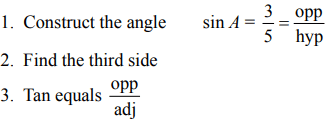
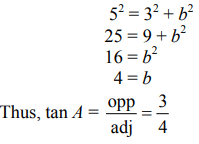
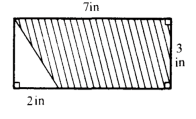
Q8: What is the area of the shaded portion?
 View Answer
View AnswerAns: The area of the shaded portion equals the area of the rectangle minus the area of the triangle. Area of rectangle = length × width = 7 inches × 3 inches = 21 square inches. Area of triangle = 1/2 × base × height =1/2 × 2 inches × 3 inches = 3square inches. Area of shaded region = 21square inches – 3 square inches = 18 squareinches. To solve this problem: (1) Find the areaof the outside, larger figure; (2) Find the area ofthe smaller, undefined figure; (3) Subtract thearea of the unshaded figure from the area of theoutside larger figure.
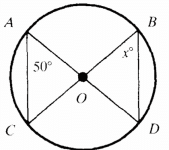
Q9: Inscribed ∠CAD measures 50°. Find the inscribed angle whose measure is x.
 View Answer
View AnswerAns:
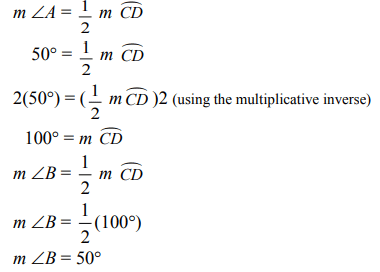
Therefore, x = 50°
The measures of two inscribed angles are equal if they intercept the same arc.
Q10: O is the center. Chords  form aninscribed angle of 30°. Find the central anglewhose measure is x
form aninscribed angle of 30°. Find the central anglewhose measure is x
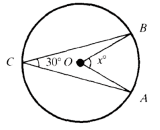
 View Answer
View AnswerAns:

|
144 videos|100 docs|61 tests
|
FAQs on Quant Practice Questions for ACT - 3 - Mathematics for ACT
| 1. How can I improve my quant score on the ACT? |  |
| 2. What are some common topics covered in the quant section of the ACT? |  |
| 3. Are there any strategies for managing time during the quant section of the ACT? |  |
| 4. How can I stay calm and focused during the quant section of the ACT? |  |
| 5. Are there any resources available for additional practice for the quant section of the ACT? |  |





















