Euler's Equation of Motion | Civil Engineering Optional Notes for UPSC PDF Download
| Table of contents |

|
| Euler’s Equation of Motion |

|
| What are Euler’s Equations in Fluid Dynamics? |

|
| Derive Euler’s Equation of Motion |

|
| Inviscid Approximation |

|
Euler’s Equation of Motion
Euler's equation of motion describes the behavior of a steady flow of an ideal fluid along a streamline. It relates the fluid's velocity, pressure, and density. Based on Newton's Second Law of Motion, which states that linear momentum is conserved in the absence of external forces, Euler's equation establishes a balance between the forces acting on a fluid element.The Bernoulli equation, which is derived from Euler's equation, represents the conservation of energy per unit weight of the fluid along a streamline. By integrating Euler's equation along a streamline and assuming the fluid is inviscid and incompressible, the Bernoulli equation provides a useful relationship between the velocity, pressure, and elevation of a fluid element in a steady flow.
Assumptions in Euler’s Equation of Motion
Euler's Equation of Motion is derived based on several assumptions:Non-viscous Flow: The fluid is assumed to have no viscosity, meaning there are no frictional losses within the fluid.
Uniform and Incompressible Substance: The fluid is assumed to be uniform, meaning its properties (density, velocity, etc.) do not vary significantly over the region of interest. Additionally, the fluid is assumed to be incompressible, meaning its density remains constant.
Steady Flow: The flow is assumed to be steady, meaning the velocity of the fluid particles at any point does not change with time.
Streamlined Flow: The flow is assumed to be streamlined, meaning the fluid flows smoothly without turbulence.
Constant Velocity Over a Section: The velocity of the fluid is assumed to be constant over a given section.
No External Forces Except Gravity and Pressure: The fluid is assumed to be under the influence of gravity and pressure forces only, with no other external forces affecting the flow.
These assumptions allow for the simplification of the fluid dynamics equations, leading to the derivation of Euler's Equation of Motion, which describes the balance between the pressure gradient force and the inertial forces in a fluid flow.
What are Euler’s Equations in Fluid Dynamics?
Euler’s equation of motion is the equation of motion and continuity that deal with a purely theoretical fluid dynamics problem known as inviscid flow. Although some very low-viscosity incompressible fluids, like water or alcohol, can be addressed in specific flow regimes, Euler’s equation of motion real fluids are nevertheless viscous.Due to this, Euler’s equations describe an ideal situation where fluid drag and energy dissipation are low, which is nonphysical and cannot occur in the real world. To approach Euler’s equation of motion, we can estimate the Navier-Stokes equations with extremely low viscosity.

Derive Euler’s Equation of Motion
We shall simply consider gravity and pressure forces in Euler’s equation of motion. Other factors will be ignored.Assumptions:
As stated here, the following presumptions are the foundation for Euler’s equation of motion.
- The fluid has no viscosity. Frictional losses won’t exist at all.
- The substance is uniform and incompressible.
- The fluid moves steadily, continuously, and in a streamline.
- The section’s fluid flow velocity is consistent.
- Only the forces of gravity and pressure will be considered.
Imagine a fluid moving from point A to point B, and consider a very small cylindrical portion of this fluid flow with length dS and cross-sectional area dA, as shown in the figure below.
Consider the forces on the cylinder: Pressure force PdA, in the direction of fluid flow.
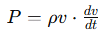
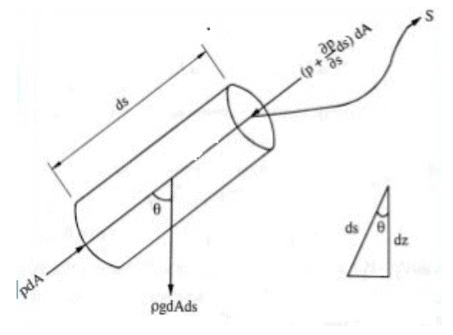
Let’s assume that the angle between the fluid flow direction and the fluid element’s weight action line is θ.
As previously stated, Euler’s equation of motion is founded on the fundamental premise of Newton’s second law of motion. As a result, we can put the following equation here:
Net force in the direction of S over the fluid element = mass of the fluid element x acceleration in the direction of S.

 |
Download the notes
Euler's Equation of Motion
|
Download as PDF |
Inviscid Approximation
In fluid dynamics, the inviscid approximation is used to describe flows where the effects of viscosity are negligible compared to other forces, such as inertial or pressure forces. This approximation is often applied in aerodynamics, where the flow of air around objects like aircraft wings can be effectively modeled using Euler's equations, which neglect viscosity.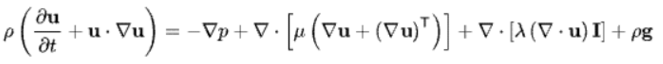
The Navier-Stokes equations describe the motion of viscous fluids and include terms that account for viscosity. When the effects of viscosity are negligible, these terms can be dropped, simplifying the equations to Euler's equations. This simplification is valid in many aerodynamic applications where the Reynolds number (a dimensionless quantity representing the ratio of inertial forces to viscous forces) is large, indicating a flow regime dominated by inertia.
By neglecting viscosity, Euler's equations provide a simpler and more computationally efficient model for analyzing aerodynamic flows, allowing engineers to quickly estimate important flow characteristics like lift and drag. However, it's important to note that Euler's equations are not applicable in all fluid flow scenarios, especially those involving boundary layers and viscous effects.
|
350 videos|464 docs|2 tests
|
FAQs on Euler's Equation of Motion - Civil Engineering Optional Notes for UPSC
| 1. What is Euler's Equation of Motion in fluid dynamics? |  |
| 2. What are Euler's Equations in Fluid Dynamics used for? |  |
| 3. How can Euler's Equation of Motion be derived? |  |
| 4. What is the Inviscid Approximation in Euler's Equation of Motion? |  |
| 5. How is Euler's Equation of Motion used in the UPSC exam? |  |


















