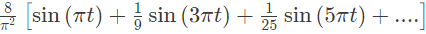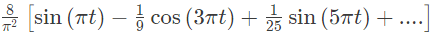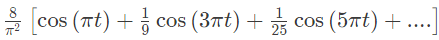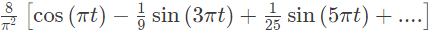Q1: The discrete time Fourier series representation of a signal x[n] with period N is written as 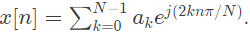 A discrete time periodic signal with period N = 3, has the non-zero Fourier series coefficients: a−3 = 2 and a4 = 1. The signal is (2022)
A discrete time periodic signal with period N = 3, has the non-zero Fourier series coefficients: a−3 = 2 and a4 = 1. The signal is (2022)
(a) 
(b) 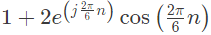
(c) 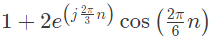
(d) 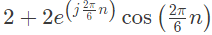
Ans: (b)
Sol: 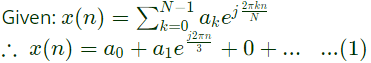 We have,
We have,
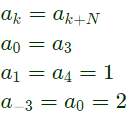 Put n = 0 in eq. (1)
Put n = 0 in eq. (1)
x(0) = a0+a1 = 2+1 = 3
Put n = 1 in eq. (1)
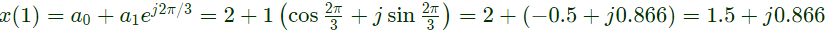 These two conditions satisfy by the option (B). Hence, option (B) will be correct.
These two conditions satisfy by the option (B). Hence, option (B) will be correct.
Q2: A periodic function f(t), with a period of 2π, is represented as its Fourier series,
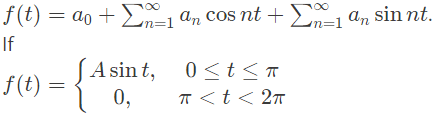 the Fourier series coefficients a1 and b1 of f(t) are (2019)
the Fourier series coefficients a1 and b1 of f(t) are (2019)
(a) 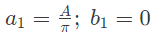
(b) 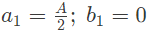
(c) 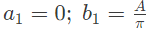
(d) 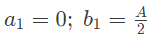
Ans: (d)
Sol: 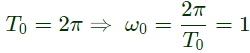

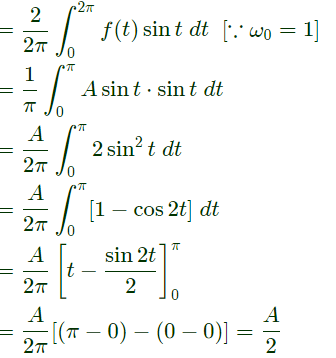
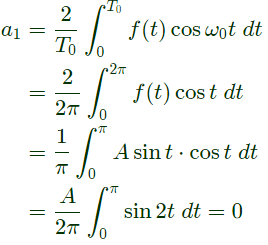
Q3: Let the signal 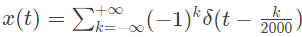 be passed through an LTI system with frequency response H(ω) , as given in the figure below
be passed through an LTI system with frequency response H(ω) , as given in the figure below
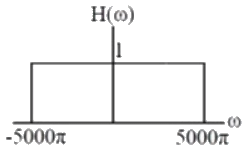 The Fourier series representation of the output is given as (SET-1 (2017))
The Fourier series representation of the output is given as (SET-1 (2017))
(a) 4000 + 4000cos(2000πt) + 4000cos(4000πt)
(b) 2000+2000cos(2000πt) + 2000cos(4000πt)
(c) 4000cos (2000πt)
(d) 2000cos (2000πt)
Ans: (c)
Sol: 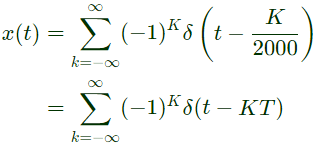
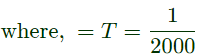
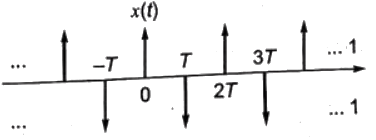 Time period:
Time period:
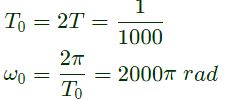 Since, x(t) is even-halt wave symmetric. So, its expansion will contain only odd harmonics of cos. Therefore, coefficient of fundamental harmonic is
Since, x(t) is even-halt wave symmetric. So, its expansion will contain only odd harmonics of cos. Therefore, coefficient of fundamental harmonic is
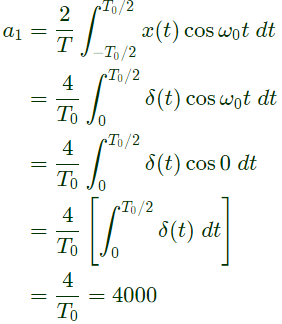 Now, frequency components available in expansion are
Now, frequency components available in expansion are
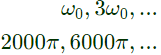 As, LTI system given in the question will pass upto 5000 π rad/sec frequency component of input.So, output will have only one component of sfrequency 2000π rad/sec
As, LTI system given in the question will pass upto 5000 π rad/sec frequency component of input.So, output will have only one component of sfrequency 2000π rad/sec
Thus, y(t) = expansion of output = a1cosω0t = 4000cos 2000πt
Q4: Consider 
Here, ⌊t⌋ represents the largest integer less than or equal to t and ⌈t⌉ denotes the smallest integer greater than or equal to t. The coefficient of the second harmonic component of the Fourier series representing g(t) is _________. (SET-1 (2017))
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (a)
Sol: Given that, 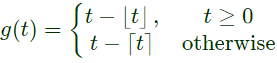
where,
⌊t⌋= greatest integer less than or equal to 't'.
⌈t⌉= smallest integer greater than or equal to 't'.
Now,
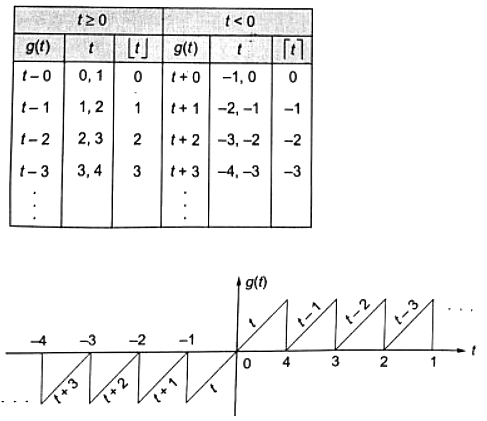 Since, g(t) is nonperiodic. So, there is no Fourier series expansion of this signal and hence no need to calculate harmonic here.
Since, g(t) is nonperiodic. So, there is no Fourier series expansion of this signal and hence no need to calculate harmonic here.
Q5: Let f(x) be a real, periodic function satisfying f(-x) = -f(x). The general form of its Fourier series representation would be (SET-2 (2016))
(a) 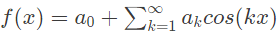
(b) 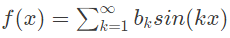
(c) 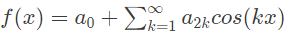
(d) 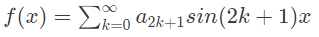
Ans: (b)
Sol: Given that,
f(−x) = −f(x)
So, function is an odd function.
So, the fourier series will have sine term only. So,
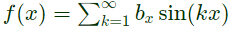
Q6: The signum function is given by
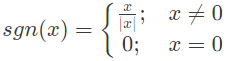 The Fourier series expansion of sgn(cos(t)) has (SET-1(2015))
The Fourier series expansion of sgn(cos(t)) has (SET-1(2015))
(a) only sine terms with all harmonics
(b) only cosine terms with all harmonics.
(c) only sine terms with even numbered harmonics.
(d) only cosine terms with odd numbered harmonics.
Ans: (d)
Sol: 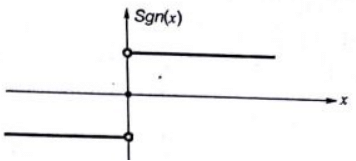 So, cos(t) is
So, cos(t) is
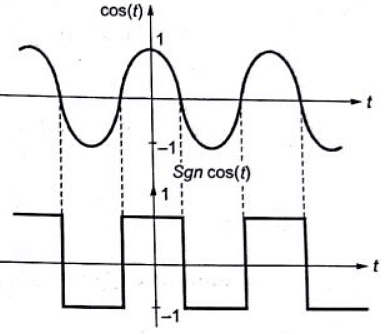 So, sgn(cos t) is a rectangular signal which is even and has half wave symmetry.
So, sgn(cos t) is a rectangular signal which is even and has half wave symmetry.
So, Fourier series will have only cosine terms with add harmonics only.
Q7: Let g : [0, ∞) → [0, ∞) be a function defined by g(x) = x-[x], where [x] represents the integer part of x . (That is, it is the largest integer which is less than or equal to x ). The value of the constant term in the Fourier series expansion of g(x) is____. (SET-1 (2014))
(a) 0
(b) 0.5
(c) 0.75
(d) 1
Ans: (b)
Sol: Given function g(t) = x−[x]
where, [x] is a integer part of x
Then function g(x) will be
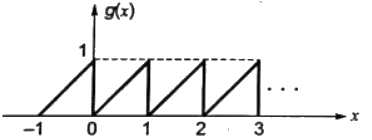 The value of the constant term (or) dc term in the Fourier series expansion of g(x) is
The value of the constant term (or) dc term in the Fourier series expansion of g(x) is
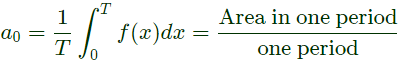
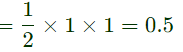
Q8: For a periodic square wave, which one of the following statements is TRUE ? (SET-1 (2014))
(a) The Fourier series coefficients do not exist
(b) The Fourier series coefficients exist but the reconstruction converges at no point
(c) The Fourier series coefficients exist but the reconstruction converges at most point
(d) The Fourier series coefficients exist and the reconstruction converges at every point.
Ans: (c)
Sol: 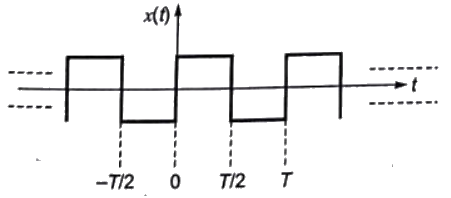
Reconstruction of signal by its Fourier series coefficient is not possible at those points where signal is discontinuous.
In the above figure, at integer multiples of 'T/2', signal recovery is not possible by using its coefficient.
Therefore, reconstruction of x(t) by using its coefficient is possible at most of the points except those instants where x(t) is discontinous.
Q9: For a periodic signal
v(t) = 30sin100t + 10cos300t + 6sin(500t + π/4),
the fundamental frequency in rad/s (2013)
(a) 100
(b) 300
(c) 500
(d) 1500
Ans: (a)
Q10: The fourier series expansion  of the periodic signal shown below will contain the following nonzero terms (2011)
of the periodic signal shown below will contain the following nonzero terms (2011)
 (a) a0 and bn, n = 1, 3, 5,... ∞
(a) a0 and bn, n = 1, 3, 5,... ∞
(b) a0 and an, n = 1, 2, 3 ,... ∞
(c) a0, an and bn, n = 1, 3, 5,... ∞
(d) a0 and an, n = 1, 3, 5 ,... ∞
Ans: (d)
Sol: Let, x(t) = Even and Hws
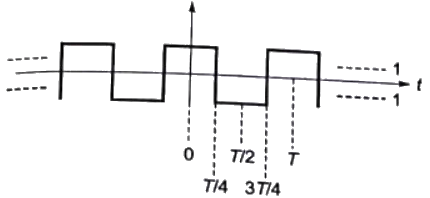 Fourier series expansion of x(t) contains cos terms with odd harmonics.
Fourier series expansion of x(t) contains cos terms with odd harmonics.
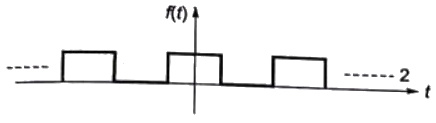 Now, f(t) = 1 + x(t)
Now, f(t) = 1 + x(t)
Fourier series of f(t) contains dc and cos terms with odd harmonics.
Q11: The second harmonic component of the periodic waveform given in the figure has an amplitude of
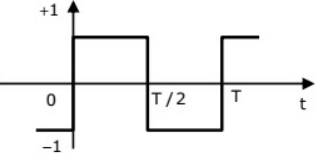 (a) 0
(a) 0
(b) 1
(c) 2/π
(d) √5
Ans: (a)
Sol: The given signal is odd as wel as having half wave symmetry.
So, it has only sine terms with odd harmonics. So, for second harmonic term amplitude = 0.
Q12: The Fourier Series coefficients of a periodic signal x(t), expressed as 𝑥(𝑡) = 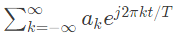 are given by a−2 = 2−j1, 𝑎−1 = 0.5 + 𝑗0.2, a0 = j2, a1 = 0.5− j0.2, 𝑎2 = 2+𝑗1 and ak = 0 for ∣k∣ > 2 Which of the following is true ? (2009)
are given by a−2 = 2−j1, 𝑎−1 = 0.5 + 𝑗0.2, a0 = j2, a1 = 0.5− j0.2, 𝑎2 = 2+𝑗1 and ak = 0 for ∣k∣ > 2 Which of the following is true ? (2009)
(a) x(t) has finite energy because only finitely many coefficients are non-zero
(b) x(t) has zero average value because it is periodic
(c) The imaginary part of x(t) is constant
(d) The real part of x(t) is even
Ans: (c)
Sol: 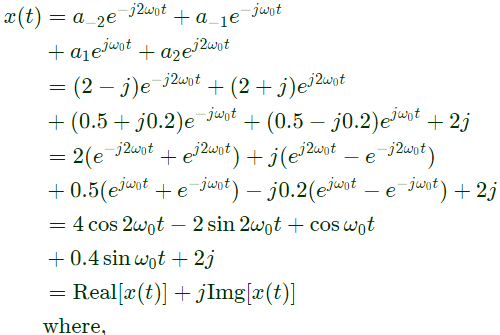
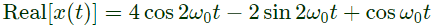

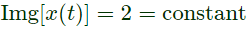
Q13: Let x(t) be a periodic signal with time period T, Let 𝑦(𝑡) = x(t − t0) + x(t + t0) for some t0. The Fourier Series coefficients of y(t) are denoted by bk. If bk = 0 for all odd k , then t0 can be equal to (2008 )
(a) T/8
(b) T/4
(c) T/2
(d) 2T
Ans: (b)
Sol: y(t) = x(t − t0) + x(t + x0)
Since, x(t) is periodic with period T.
Therefore, x(t − t0) and x(t + t0) will also be periodic with period T.
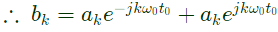 ak is Fourier series coefficient of signal x(t)
ak is Fourier series coefficient of signal x(t)
therefore,
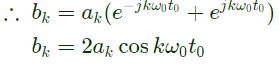
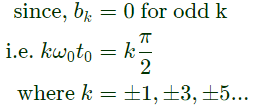
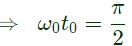
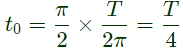
Q14: A signal x(t) is given by
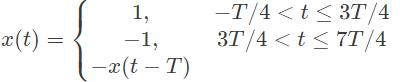 Which among the following gives the fundamental fourier term of x(t)? (2007)
Which among the following gives the fundamental fourier term of x(t)? (2007)
(a) 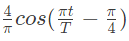
(b) 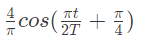
(c) 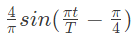
(d) 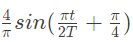
Ans: (a)
Sol: According to defination of signal given in question the x(t) will be as
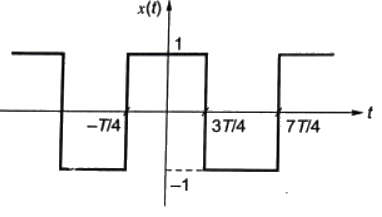 So it is periodic with period,
So it is periodic with period,
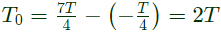 Therefore, fundamental angular frequency
Therefore, fundamental angular frequency
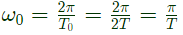 Now,
Now,
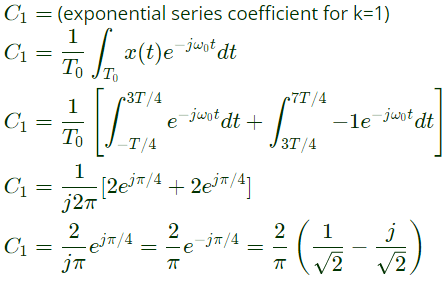 Comparing it with
Comparing it with
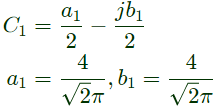
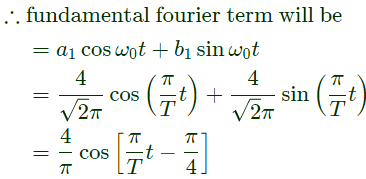
Q15: x(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π(2k)/T; k = 1, 2... Also, no sine terms are present. Then x(t) satisfies the equation (2006)
(a) x(t) = −x(t − T)
(b) x(t) = x(T − t) = −x(−t)
(c) x(t) = x(T − t) = −x(t − T/2)
(d) x(t) = x(t − T) = x(t − T/2)
Ans: (c)
Sol: Since trigonometric fourier series has no sine terms and has only cosine terms therefore this will be an even signal i.e. it will satisfy.
x(t) = x(−t)
or, we can write,
x(t − T) = x(−t + T)
but signal is periodic with period T.
therefore x(t − T) = x(t)
therefore, x(t) = x(T − t)...(i)
Now, since signal contains only odd harmonics i.e. no terms of frequency
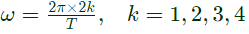 i.e. no even harmonics.
i.e. no even harmonics.
This means signal contains half wave symmetry
this implies that,
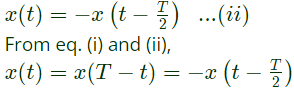
Q16: The Fourier series for the function f(x) = sin2x is (2005)
(a) sinx + sin2x
(b) 1 − cos2x
(c) sin2x + cos2x
(d) 0.5 − 0.5cos2x
Ans: (d)
Sol: f(n) = sin2x
for finding the fourier series expansion
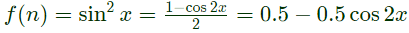
Q17: For the triangular wave from shown in the figure, the RMS value of the voltage is equal to (2005)
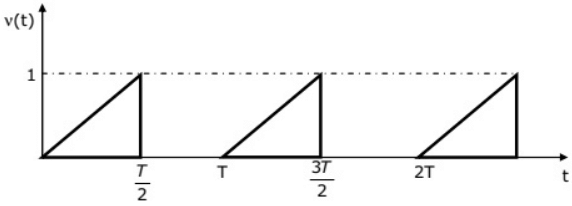 (a)
(a) 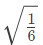
(b) 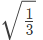
(c) 1/3
(d) 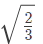
Ans: (a)
Sol: From the wave symmetry,
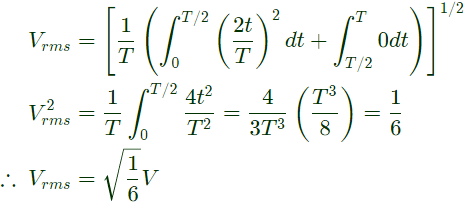
Q18: The rms value of the periodic waveform given in figure is
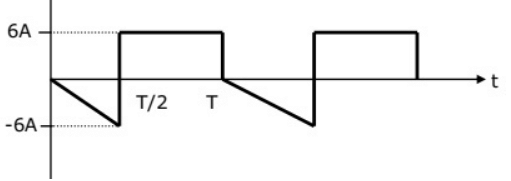 (a) 2√6 A
(a) 2√6 A
(b) 6√2 A
(c) √4/3 A
(d) 1.5 A
Ans: (a)
Sol: 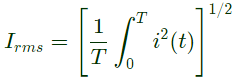
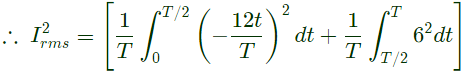
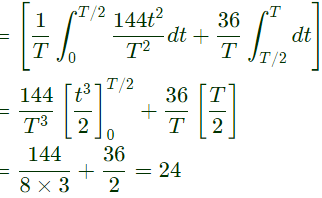
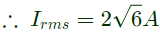
Q19: Fourier Series for the waveform, f(t) shown in figure is (2002)
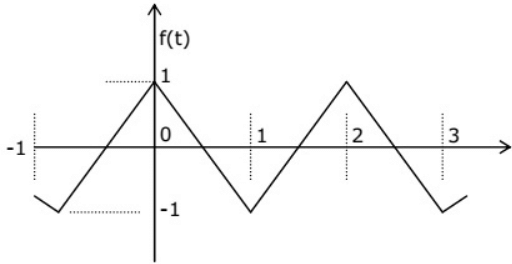 (a)
(a) 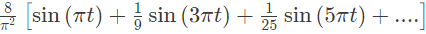
(b) 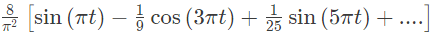
(c) 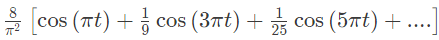
(d) 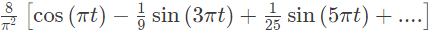
Ans: (c)
Sol: ∵ f(t) is an even function with half waves symmetry,
∴ dc term as well as sine terms = 0
Only the cosine terms with odd harmonics will be present.
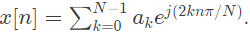 A discrete time periodic signal with period N = 3, has the non-zero Fourier series coefficients: a−3 = 2 and a4 = 1. The signal is (2022)
A discrete time periodic signal with period N = 3, has the non-zero Fourier series coefficients: a−3 = 2 and a4 = 1. The signal is (2022)
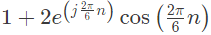
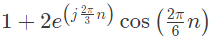
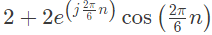
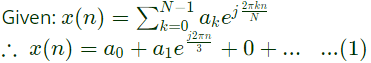 We have,
We have,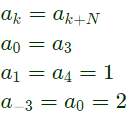 Put n = 0 in eq. (1)
Put n = 0 in eq. (1)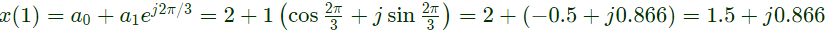 These two conditions satisfy by the option (B). Hence, option (B) will be correct.
These two conditions satisfy by the option (B). Hence, option (B) will be correct.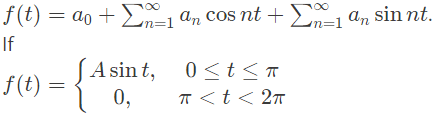 the Fourier series coefficients a1 and b1 of f(t) are (2019)
the Fourier series coefficients a1 and b1 of f(t) are (2019)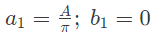
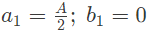
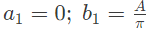
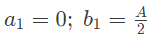
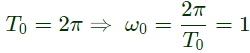

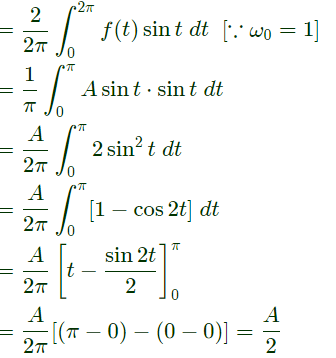
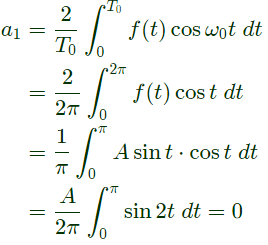
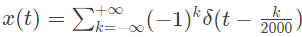 be passed through an LTI system with frequency response H(ω) , as given in the figure below
be passed through an LTI system with frequency response H(ω) , as given in the figure below The Fourier series representation of the output is given as (SET-1 (2017))
The Fourier series representation of the output is given as (SET-1 (2017))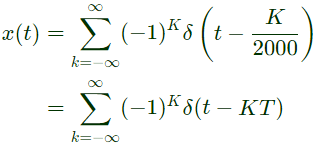
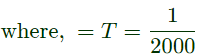
 Time period:
Time period: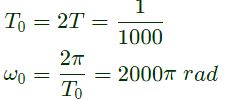 Since, x(t) is even-halt wave symmetric. So, its expansion will contain only odd harmonics of cos. Therefore, coefficient of fundamental harmonic is
Since, x(t) is even-halt wave symmetric. So, its expansion will contain only odd harmonics of cos. Therefore, coefficient of fundamental harmonic is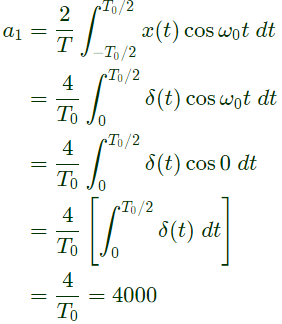 Now, frequency components available in expansion are
Now, frequency components available in expansion are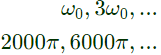 As, LTI system given in the question will pass upto 5000 π rad/sec frequency component of input.So, output will have only one component of sfrequency 2000π rad/sec
As, LTI system given in the question will pass upto 5000 π rad/sec frequency component of input.So, output will have only one component of sfrequency 2000π rad/sec
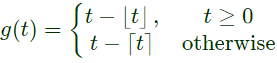
 Since, g(t) is nonperiodic. So, there is no Fourier series expansion of this signal and hence no need to calculate harmonic here.
Since, g(t) is nonperiodic. So, there is no Fourier series expansion of this signal and hence no need to calculate harmonic here.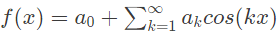
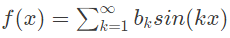
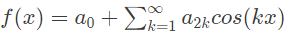
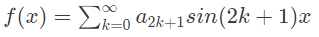
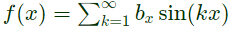
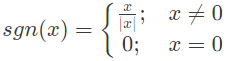 The Fourier series expansion of sgn(cos(t)) has (SET-1(2015))
The Fourier series expansion of sgn(cos(t)) has (SET-1(2015)) So, cos(t) is
So, cos(t) is So, sgn(cos t) is a rectangular signal which is even and has half wave symmetry.
So, sgn(cos t) is a rectangular signal which is even and has half wave symmetry. The value of the constant term (or) dc term in the Fourier series expansion of g(x) is
The value of the constant term (or) dc term in the Fourier series expansion of g(x) is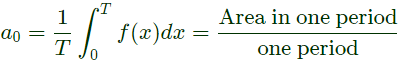
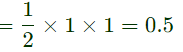

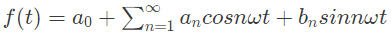 of the periodic signal shown below will contain the following nonzero terms (2011)
of the periodic signal shown below will contain the following nonzero terms (2011) (a) a0 and bn, n = 1, 3, 5,... ∞
(a) a0 and bn, n = 1, 3, 5,... ∞ Fourier series expansion of x(t) contains cos terms with odd harmonics.
Fourier series expansion of x(t) contains cos terms with odd harmonics. Now, f(t) = 1 + x(t)
Now, f(t) = 1 + x(t)  (a) 0
(a) 0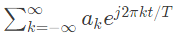 are given by a−2 = 2−j1, 𝑎−1 = 0.5 + 𝑗0.2, a0 = j2, a1 = 0.5− j0.2, 𝑎2 = 2+𝑗1 and ak = 0 for ∣k∣ > 2 Which of the following is true ? (2009)
are given by a−2 = 2−j1, 𝑎−1 = 0.5 + 𝑗0.2, a0 = j2, a1 = 0.5− j0.2, 𝑎2 = 2+𝑗1 and ak = 0 for ∣k∣ > 2 Which of the following is true ? (2009)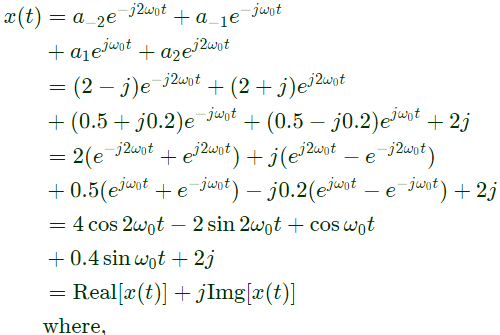

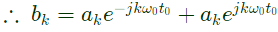 ak is Fourier series coefficient of signal x(t)
ak is Fourier series coefficient of signal x(t)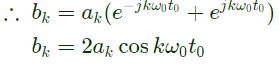
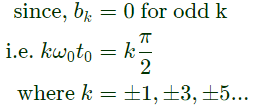
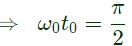
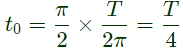
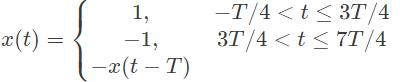 Which among the following gives the fundamental fourier term of x(t)? (2007)
Which among the following gives the fundamental fourier term of x(t)? (2007)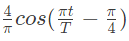
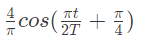
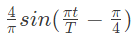
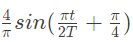
 So it is periodic with period,
So it is periodic with period,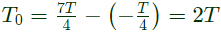 Therefore, fundamental angular frequency
Therefore, fundamental angular frequency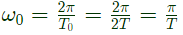 Now,
Now,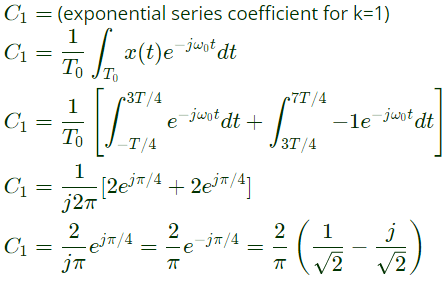 Comparing it with
Comparing it with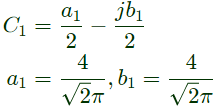
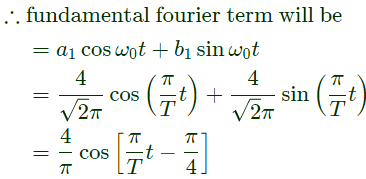
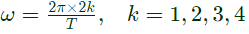 i.e. no even harmonics.
i.e. no even harmonics.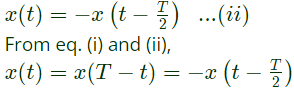
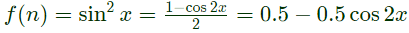
 (a)
(a) 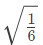
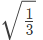
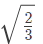
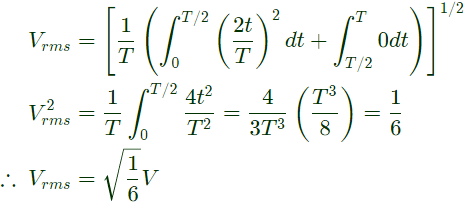
 (a) 2√6 A
(a) 2√6 A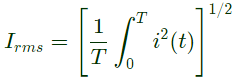
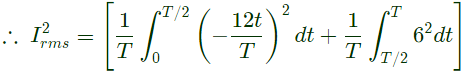
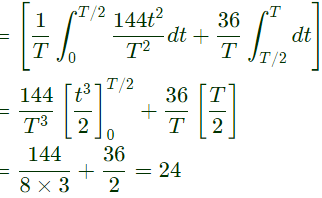
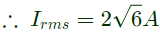
 (a)
(a)