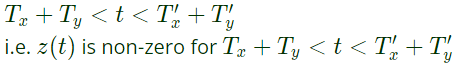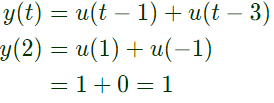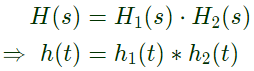Q1: The input x(t) and the output y(t) of a system are related as (2024)
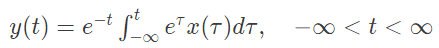 The system is (2024)
The system is (2024)
(a) nonlinear
(b) linear and time-invariant
(c) linear but not time-invariant
(d) noncasual
Ans: (b)
Sol: System will follow law of superposition. Therefore, system will be linear.
Time-invariance check:
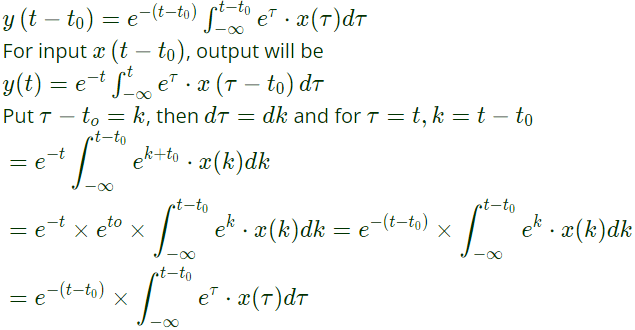 Since,
Since,
y(t) = y(t − t0)
So, the system is time-invariant.
Q2: Which of the following statement(s) is/are true? (2023)
(a) If an LTI system is causal, it is stable
(b) A discrete time LTI system is causal if and only if its response to a step input u[n] is 0 for n < 0
(c) If a discrete time LTI system has an impulse response h[n] of finite duration the system is stable
(d) If the impulse response 0 < ∣h[n]∣ < 1 for all n, then the LTI system is stable.
Ans: (b)
Sol: For causal system, impuse response
h(n) = 0; n < 0
Therefore, for step input also
h(n) = 0; n < 0
Q3: Consider the system as shown below
 where y(t) = x(et). The system is (2022)
where y(t) = x(et). The system is (2022)
(a) linear and causal.
(b) linear and non-causal.
(c) non-linear and causal
(d) non-linear and non-causal
Ans: (b)
Sol: We know, a linear system follows the law of superposition.
It is a combination of two laws:
(i) Law of additivity:
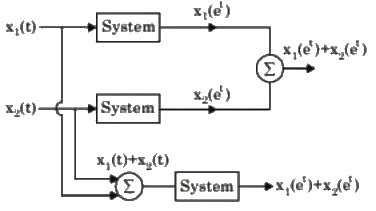 Both results are same, hence, it follows law of additivity.
Both results are same, hence, it follows law of additivity.
(ii) Law of Homogeneity:
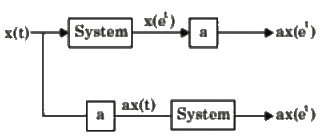 Here also both results are same, hence it follows law of Homogeneity.
Here also both results are same, hence it follows law of Homogeneity.
Therefore, System is linear.
We know, a causal system is independent of future values of input at each & every instant of time them system will be causal.
Given : y(t) = x(et)
Put t = 0
y(0) = x(e0) = x(1)
Because its depends on future value.
Therefore, system is non-causal.
Q4: Let a causal LTI system be governed by the following differential equation 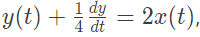 where x(t) and x(t) are the input and output respectively. Its impulse response is (2022)
where x(t) and x(t) are the input and output respectively. Its impulse response is (2022)
(a) 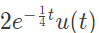
(b) 
(c) 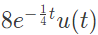
(d) 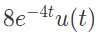
Ans: (d)
Sol: Given:
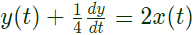 Taking Laplace transform,
Taking Laplace transform,
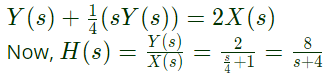 Taking inverse Laplace, transform,
Taking inverse Laplace, transform,
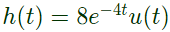
Q5: If the input x(t) and output y(t) of a system are related as y(t) = max(0, x (t)), then the system is (2021)
(a) linear and time-variant
(b) linear and time-invariant
(c) non-linear and time-variant
(d) non-linear and time-invariant
Ans: (d)
Sol: 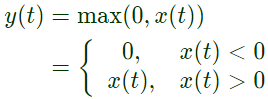
 Linearity check:
Linearity check:
at input x1(t) = −2, output y1(t) = 0
at input x2(t) = 1, output y2(t) = 1
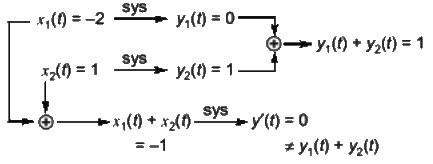 ∴ system is non-linear because it violates law of additivity.
∴ system is non-linear because it violates law of additivity.
Check for time-invariance :
Delayed O/P:
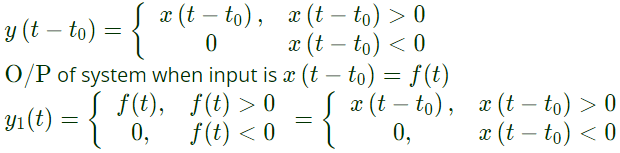 Therefore, system is time-invariant.
Therefore, system is time-invariant.
Q6: Which of the following options is true for a linear time-invariant discrete time system that obeys the difference equation:
y[n] − ay[n − 1] = b0x[n] − b1x[n − 1] (2020)
(a) y[n] is unaffected by the values of x[n − k]; k > 2
(b) The system is necessarily causal.
(c) The system impulse response is non-zero at infinitely many instants.
(d) When x[n] = 0, n < 0, the function y[n]; n > 0 is solely determined by the function x[n].
Ans: (c)
Sol: 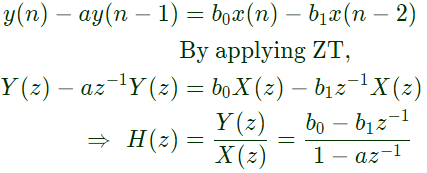 By taking right-sided inverse ZT,
By taking right-sided inverse ZT,
h(n) = b0anu(n)−b1an−1u(n − 1)
By taking left-sided inverse ZT,
h(n) = −b0anu(−n − 1) + b1an−1u(−n)
Thus system is not necessarily causal.
The impulse response is non-zero at infinitely many instants.
Q7: A continuous-time input signal x(t) is an eigenfunction of an LTI system, if the output is (2018)
(a) k x (t) , where k is an eigenvalue
(b) ke jωt x(t), where k is an eigenvalue and ejωt is a complex exponential signal
(c) x(t) ejωt, where ejωt is a complex exponential signal
(d) k H(ω) ,where k is an eigenvalue and H(ω) is a frequency response of the system
Ans: (a)
Sol: Eigen function is a type of input for which output is constant times of input.
i.e.
 Where,
Where,
x(t) = System input = eigen function
H(s) = transfer function of system
y(t) = system output
Here,
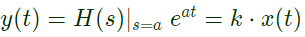 where,
where,
k = eigen-value = H(s)∣s = a
x(t) = eigen-function input
Q8: Let z(t) = x(t) * y(t) , where "*" denotes convolution. Let c be a positive real-valued constant. Choose the correct expression for z(ct). (SET-1 (2017))
(a) c x(ct)*y(ct)
(b) x(ct)*y(ct)
(c) c x(t)*y(ct)
(d) c x(t)*y(ct)
Ans: (a)
Sol: Time scaling property of convolution.
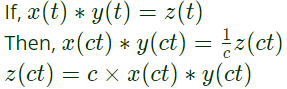
Q9: Consider a causal LTI system characterized by differential equation 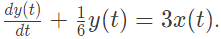 The response of the system to the input
The response of the system to the input 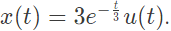 where u(t) denotes the unit step function, is (SET-2 (2016))
where u(t) denotes the unit step function, is (SET-2 (2016))
(a) 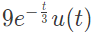
(b) 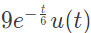
(c) 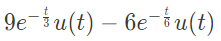
(d) 
Ans: (d)
Sol: The differential equation
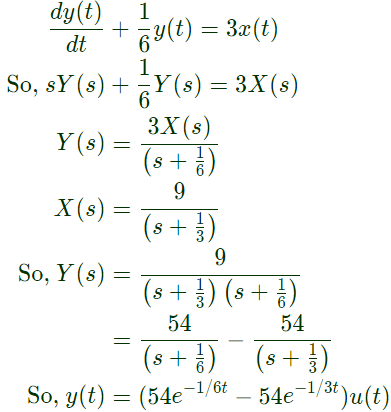
Q10: The output of a continuous-time, linear time-invariant system is denoted by T{x(t)} where x(t) is the input signal. A signal z(t) is called eigen-signal of the system T, when T{z(t)} = γz(t), where γ is a complex number, in general, and is called an eigenvalue of T. Suppose the impulse response of the system T is real and even. Which of the following statements is TRUE? (SET-1 (2016))
(a) cos(t) is an eigen-signal but sin(t) is not
(b) cos(t) and sin(t) are both eigen-signals but with different eigenvalues
(c) sin(t) is an eigen-signal but cos(t) is not
(d) cos(t) and sin(t) are both eigen-signals with identical eigenvalues
Ans: (d)
Sol: Given that impulse response is real and even, Thus H(jω) will also be real and even.
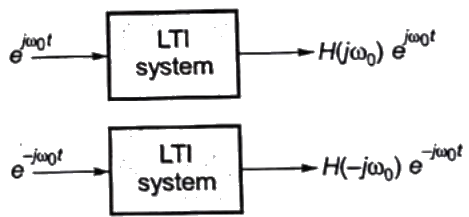 Since, H(jω) is real and even thus,
Since, H(jω) is real and even thus,
 So, sin(t) and cos(t) are eigen signal with same eigen values.
So, sin(t) and cos(t) are eigen signal with same eigen values.
Q11: Consider the following state-space representation of a linear time-invariant system.
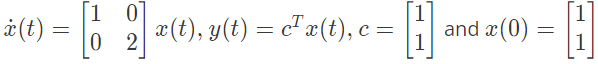 The value of y(t) for t = loge2 is______. (SET-1 (2016))
The value of y(t) for t = loge2 is______. (SET-1 (2016))
(a) 4
(b) 5
(c) 6
(d) 7
Ans: (c)
Q12: Consider a continuous-time system with input x(t) and output y(t) given by
y(t) = x(t) cos(t)
This system is (SET-1 (2016))
(a) linear and time-invariant
(b) non-linear and time-invariant
(c) linear and time-varying
(d) non-linear and time-varying
Ans: (c)
Sol: 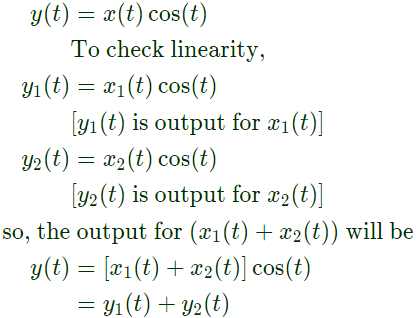 So, the system is linear, to check time invariance.
So, the system is linear, to check time invariance.
The delayed output,
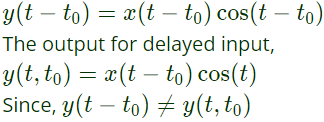 System is time varying.
System is time varying.
Q13: The following discrete-time equations result from the numerical integration of the differential equations of an un-damped simple harmonic oscillator with state variables x and y. The integration time step is h.
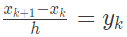
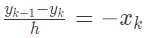 For this discrete-time system, which one of the following statements is TRUE? (SET-2 (2015))
For this discrete-time system, which one of the following statements is TRUE? (SET-2 (2015))
(a) The system is not stable for h > 0
(b) The system is stable for h > (1/π)
(c) The system is stable for 0 < h < (1/2π)
(d) The system is stable for (1/2π) < h < (1/π)
Ans: (a)
Q14: For linear time invariant systems, that are Bounded Input Bounded Output stable, which one of the following statements is TRUE? (SET-2 (2015))
(a) The impulse response will be integrable, but may not be absolutely integrable.
(b) The unit impulse response will have finite support.
(c) The unit step response will be absolutely integrable
(d) The unit step response will be bounded.
Ans: (d)
Q15: The impulse response g(t) of a system, G , is as shown in Figure (a). What is the maximum value attained by the impulse response of two cascaded blocks of G as shown in Figure (b)? (SET-1 (2015))
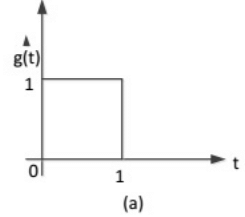
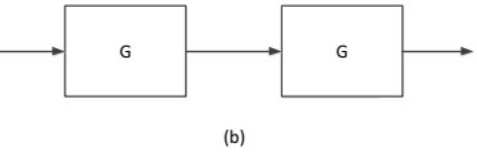
(a) 2/3
(b) 3/4
(c) 4/5
(d) 1
Ans: (d)
Sol: 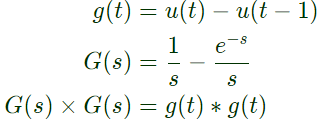
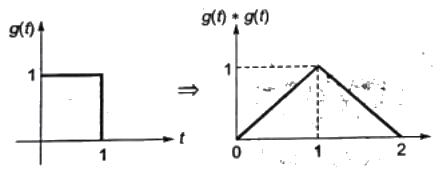 Maximum value = 1
Maximum value = 1
Q16: A moving average function is given by 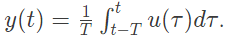 If the input u is a sinusoidal signal of frequency (1/2τ) Hz, then in steady state, the output y will lag u (in degree) by ______ . (SET-1 (2015))
If the input u is a sinusoidal signal of frequency (1/2τ) Hz, then in steady state, the output y will lag u (in degree) by ______ . (SET-1 (2015))
(a) 30
(b) 60
(c) 90
(d) 120
Ans: (c)
Sol: System input: sin ω0t
 Therefore,
Therefore,
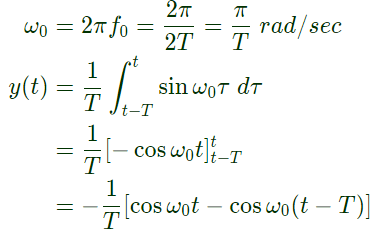
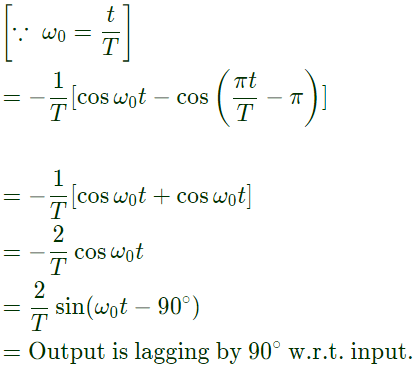
Q17: Consider an LTI system with impulse response h(t) = e−5tu(t). If the output of the system is y(t) = e−3tu(t) − e−5tu(t) then the input, x(t), is given by (SET-2 (2014))
(a) e−3t u(t)
(b) 2e−3t u(t)
(c) e−5t u(t)
(d) 2e−5t u(t)
Ans: (b)
Sol: Impulse response of an LTI system = transfer function 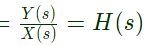
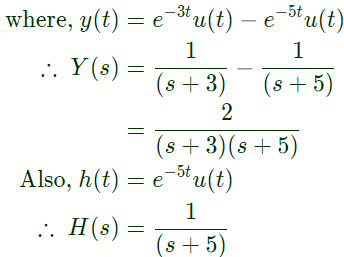
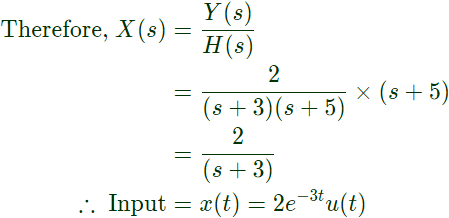
Q18: x(t) is nonzero only for Tx < t < Tx′, and similarly, y(t) is nonzero only for Ty < t < Ty′. Let z(t) be convolution of x(t) and y(t). Which one of the following statements is TRUE ? (SET-1 (2014))
(a) z(t) can be nonzero over an unbounded interval.
(b) z(t) is nonzero for t < Tx + Ty
(c) z(t) is zero outside of 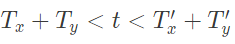
(d) z(t) is nonzero for 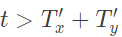
Ans: (c)
Sol: x(t) is non-zero for 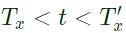 and y(t) is non-zero for
and y(t) is non-zero for 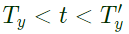
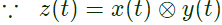 then the limits of the resultant signal is
then the limits of the resultant signal is
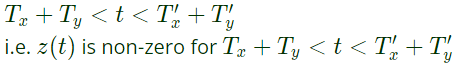
Q19: The impulse response of a continuous time system is given by h(t) = δ(t − 1)δ(t − 3). The value of the step response at t = 2 is (2013)
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (b)
Sol: For step response, impulse response can be integrated.
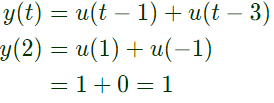
Q20: Two systems with impulse responses h1(t) and h2(t) are connected in cascade. Then the overall impulse response of the cascaded system is given by (2013)
(a) product of h1(t) and h2(t)
(b) sum of h1(t) and h2(t)
(c) convolution of h1(t) and h2(t)
(d) subtraction of h1(t) and h2(t)
Ans: (c)
Sol: In cascade connection,

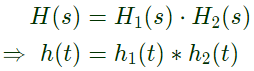
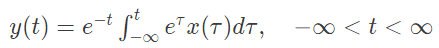 The system is (2024)
The system is (2024)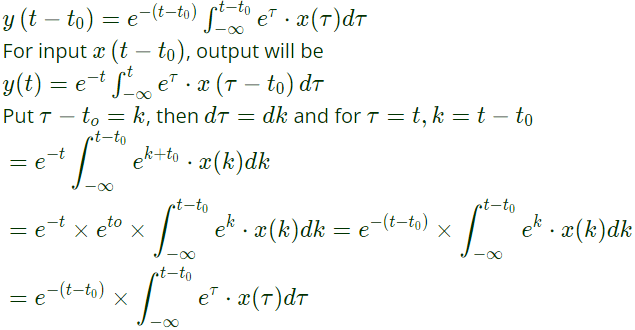 Since,
Since, where y(t) = x(et). The system is (2022)
where y(t) = x(et). The system is (2022) Both results are same, hence, it follows law of additivity.
Both results are same, hence, it follows law of additivity. Here also both results are same, hence it follows law of Homogeneity.
Here also both results are same, hence it follows law of Homogeneity.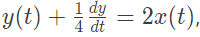 where x(t) and x(t) are the input and output respectively. Its impulse response is (2022)
where x(t) and x(t) are the input and output respectively. Its impulse response is (2022)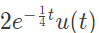

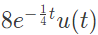
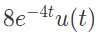
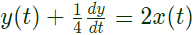 Taking Laplace transform,
Taking Laplace transform,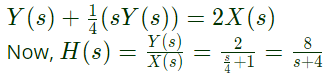 Taking inverse Laplace, transform,
Taking inverse Laplace, transform,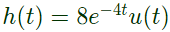
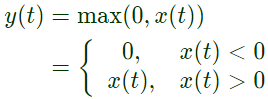
 Linearity check:
Linearity check: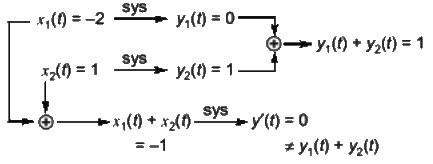 ∴ system is non-linear because it violates law of additivity.
∴ system is non-linear because it violates law of additivity. Therefore, system is time-invariant.
Therefore, system is time-invariant.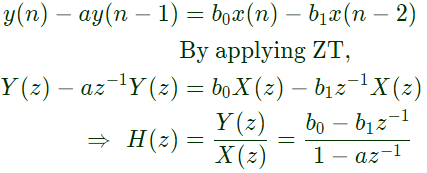 By taking right-sided inverse ZT,
By taking right-sided inverse ZT, Where,
Where,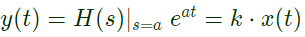 where,
where,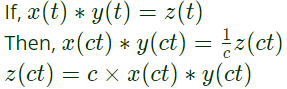
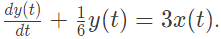 The response of the system to the input
The response of the system to the input 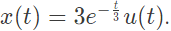 where u(t) denotes the unit step function, is (SET-2 (2016))
where u(t) denotes the unit step function, is (SET-2 (2016))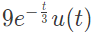
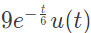
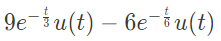

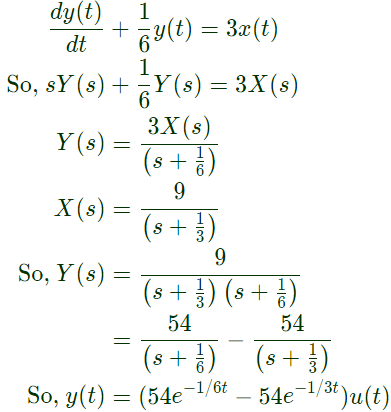
 Since, H(jω) is real and even thus,
Since, H(jω) is real and even thus, So, sin(t) and cos(t) are eigen signal with same eigen values.
So, sin(t) and cos(t) are eigen signal with same eigen values. 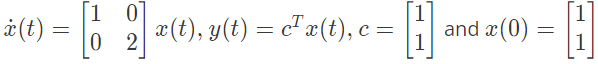 The value of y(t) for t = loge2 is______. (SET-1 (2016))
The value of y(t) for t = loge2 is______. (SET-1 (2016))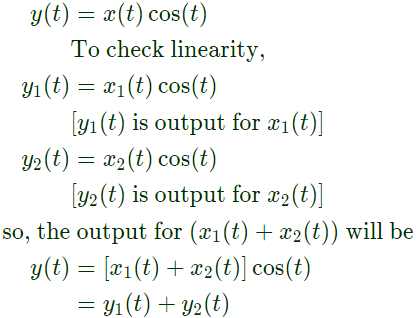 So, the system is linear, to check time invariance.
So, the system is linear, to check time invariance.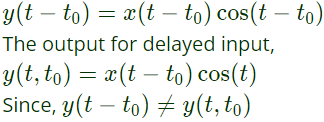 System is time varying.
System is time varying.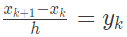
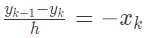 For this discrete-time system, which one of the following statements is TRUE? (SET-2 (2015))
For this discrete-time system, which one of the following statements is TRUE? (SET-2 (2015))

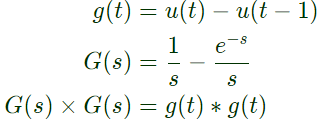
 Maximum value = 1
Maximum value = 1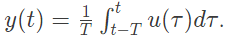 If the input u is a sinusoidal signal of frequency (1/2τ) Hz, then in steady state, the output y will lag u (in degree) by ______ . (SET-1 (2015))
If the input u is a sinusoidal signal of frequency (1/2τ) Hz, then in steady state, the output y will lag u (in degree) by ______ . (SET-1 (2015)) Therefore,
Therefore,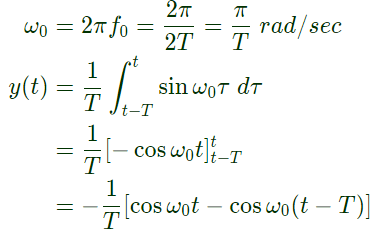
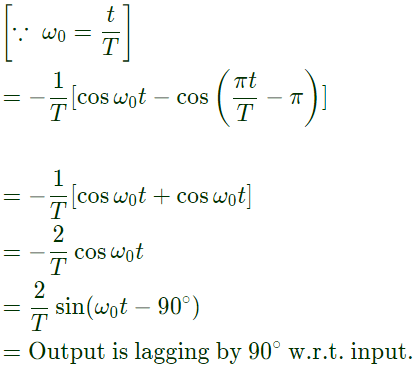
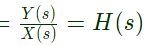
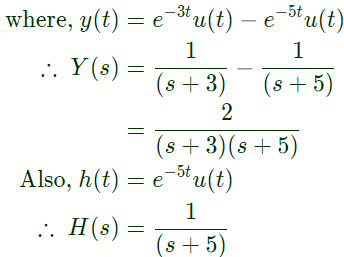
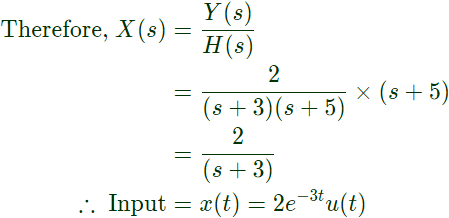
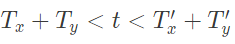
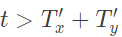
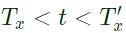 and y(t) is non-zero for
and y(t) is non-zero for 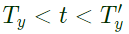
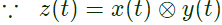 then the limits of the resultant signal is
then the limits of the resultant signal is