Q1: Let X(ω) be the Fourier transform of the signal,
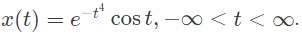 The value of the derivative of X(ω) at ω = 0 at is _____ (rounded off to 1 decimal place) (2024)
The value of the derivative of X(ω) at ω = 0 at is _____ (rounded off to 1 decimal place) (2024)
(a) 0
(b) 0.2
(c) 0.4
(d) 0.8
Ans: (a)
Sol: 
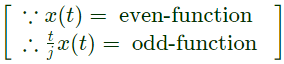
Q2: The discrete-time Fourier transform of a signal x[n] is X(Ω) = 1(1+cosΩ)e−jΩ. Consider that xp[n] is a periodic signal of period N = 5 such that
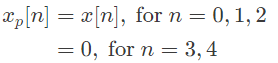 Note that
Note that 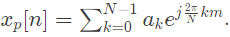 The magnitude of the Fourier series coefficient a3 is ____ (Round off to 3 decimal places). (2023)
The magnitude of the Fourier series coefficient a3 is ____ (Round off to 3 decimal places). (2023)
(a) 0.038
(b) 0.025
(c) 0.068
(d) 0.012
Ans: (a)
Sol: Given : xp(n) is a period signal of period N = 5.
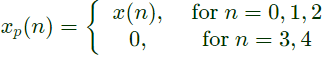
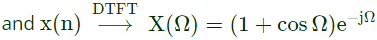 We have,
We have,
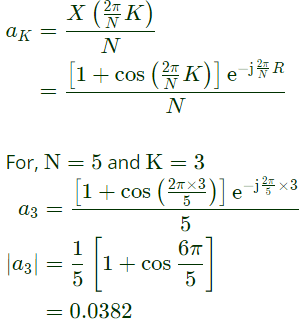
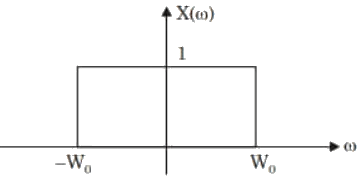
Q3: The Fourier transform X(ω) of the signal x(t) is given by
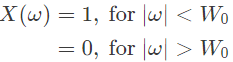 Which one of the following statements is true? (2023)
Which one of the following statements is true? (2023)
(a) x(t) tends to be an impulse as W0→∞
(b) x(0) decreases as W0 increases
(c) 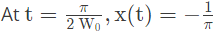 (d)
(d) 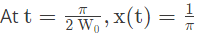 Ans: (a)
Ans: (a)
Sol: Given,
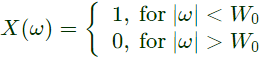
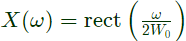
 We know,
We know,
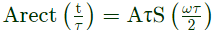 By duality,
By duality,
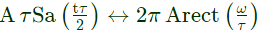 Given,
Given,
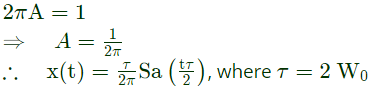 Thus,
Thus,
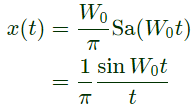
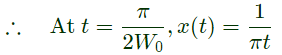 From rectangular function, At W ⇒ ∞, X(w) = 1
From rectangular function, At W ⇒ ∞, X(w) = 1
Taking inverse fourier transform x(t) = δ(t)
Option (A) will be correct.
Q4: Let an input x(t) = 2sin(10πt) + 5cos(15πt) + 7sin(42πt) + 4cos(45πt) is passed through an LTI system having an impulse response,
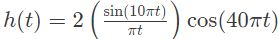 The output of the system is (2022)
The output of the system is (2022)
(a) 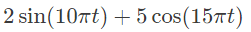
(b) 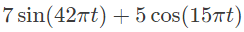
(c) 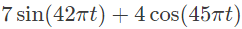
(d) 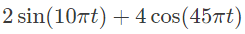
Ans: (c)
Sol: 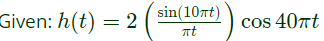 Fourier transform of signal
Fourier transform of signal 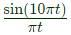 is given by
is given by
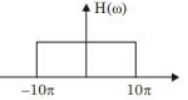 Now, impulse response
Now, impulse response
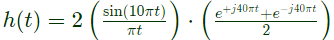 Using property,
Using property, 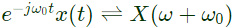
Therefore, Fourier transform of impulse response
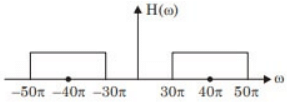 Cut-off frequencies,
Cut-off frequencies,
ωL= 30π rad/sec
ωH = 50π rad/sec
Thus, output of the system = 7sin 42πt + 4cos 45πt
Q5: Consider a continuous-time signal x(t) defined by x(t) = 0 for ∣t∣ >1, and x(t) = 1 − ∣t∣ for ∣t∣ ≤ 1. Let the Fourier transform of x(t) be defined as 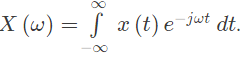 The maximum magnitude of X(ω) is _____. (2021)
The maximum magnitude of X(ω) is _____. (2021)
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
Sol: Fourier transform, 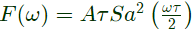
As A = 1, τ = 1
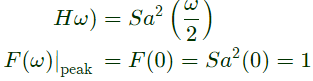 ∵ Peak value of sampling function occurs at ω = 0
∵ Peak value of sampling function occurs at ω = 0
Peak value = 1
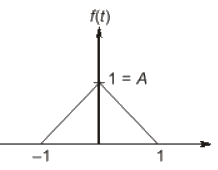
Q6: Let f(t) be an even function, i.e. f(−t) = f(t) for all t. Let the Fourier transform of f(t) be defined as 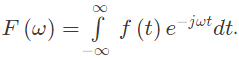 Suppose
Suppose 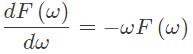 for all ω, and F(0) = 1. Then (2021)
for all ω, and F(0) = 1. Then (2021)
(a) f(0) < 1
(b) f(0) > 1
(c) f(0) = 1
(d) f(0) = 0
Ans: (a)
Sol:  The following informations are given about
The following informations are given about 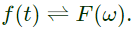
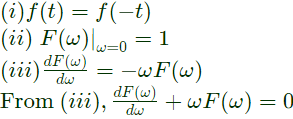 By solving the above linear differential equations, (by mathematics)
By solving the above linear differential equations, (by mathematics)
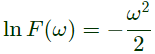 ⇒
⇒ 
Put ω = 0, F(0) = K
⇒ 1 = K (From info.
From (iv), 
As we know, 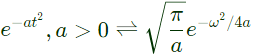
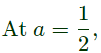
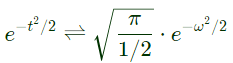
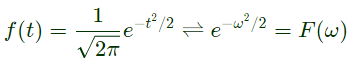 Thus,
Thus, 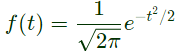
At t = 0, 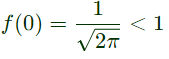
Q7: The Fourier transform of a continuous-time signal x(t) is given by 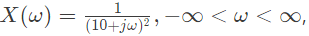
where 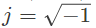 and ω denotes frequency. Then the value of |lnx(t)| at t = 1 is ___________ (up to 1 decimal place). ( ln denotes the logarithm to base e) (2018)
and ω denotes frequency. Then the value of |lnx(t)| at t = 1 is ___________ (up to 1 decimal place). ( ln denotes the logarithm to base e) (2018)
(a) 10.0
(b) 7.5
(c) 11.8
(d) 2.8
Ans: (a)
Sol: 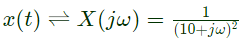 By taking inverse Fourier transform,
By taking inverse Fourier transform,
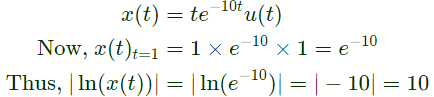
Q8: The value of the integral  is equal to (SET-2 (2016))
is equal to (SET-2 (2016))
(a) 0
(b) 0.5
(c) 1
(d) 2
Ans: (d)
Sol: The Fourier transform of

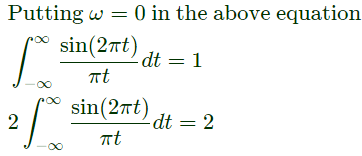
Q9: Suppose the maximum frequency in a band-limited signal x(t) is 5 kHz. Then, the maximum frequency in x(t) cos(2000πt), in kHz, is ________. (SET-2 (2016))
(a) 5
(b) 6
(c) 7
(d) 8
Ans: (b)
Sol: Maximum possible frequency of x(t)(2000πt) = f1 + f2 = 5 + 1 = 6kHz
Q10: Suppose x1(t) and x2(t) have the Fourier transforms as shown below.
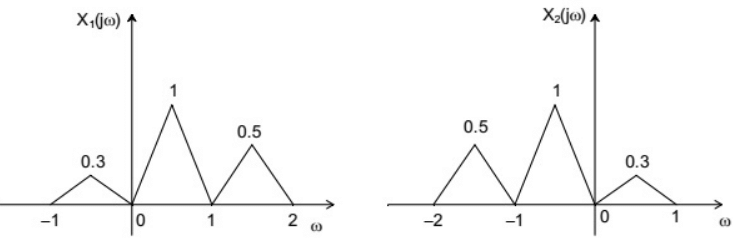 Which one of the following statements is TRUE? (SET-1 (2016))
Which one of the following statements is TRUE? (SET-1 (2016))
(a) x1(t) and x2(t) are complex and x1(t) x2(t) is also complex with nonzero imaginary part
(b) x1(t) and x2(t) are real and x1(t) x2(t) is also real
(c) x1(t) and x2(t) are complex but x1(t) x2(t) is real
(d) x1(t) and x2(t) are imaginary but x1(t) x2(t) is real
Ans: (c)
Sol: By observing X1(jω) and X2(jω), we can say that they are not conjugate symmetric. Since, the fourier transform is not conjugate symmetric the signal will not be real. So, x1(t), x2(t) are not real. Now the fourier transform of x1(t)⋅x2(t) will be 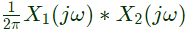 and by looking at X1(jω) and X2(jω), we can say that X1(jω)∗X2(jω) will be conjugate symmetric and thus x1(t)⋅x2(t) will be real.
and by looking at X1(jω) and X2(jω), we can say that X1(jω)∗X2(jω) will be conjugate symmetric and thus x1(t)⋅x2(t) will be real.
By observing X1(jω) and X2(jω), we can say,
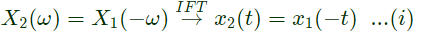 Now, X1(jω) is real. Therefore, x1(t) will be conjugate symmetric.
Now, X1(jω) is real. Therefore, x1(t) will be conjugate symmetric.
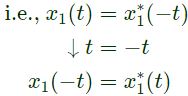

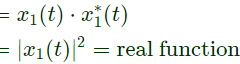
Q11: Consider a signal defined by
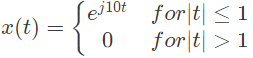 Its Fourier Transform is (SET-2 (2015))
Its Fourier Transform is (SET-2 (2015))
(a) 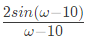
(b) 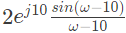
(c) 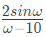
(d) 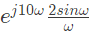
Ans: (a)
Sol: Since, 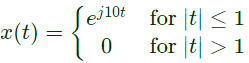
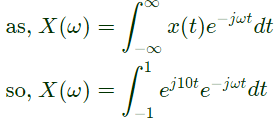
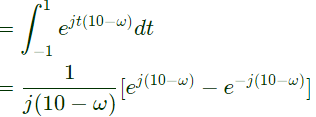
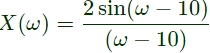
Q12: A differentiable non constant even function x(t) has a derivative y(t), and their respective Fourier Transforms are X(ω) and Y(ω). Which of the following statments is TRUE ? (SET-3 ( 2014))
(a) X(ω) and Y(ω) are both real
(b) X(ω) is real and Y(ω) is imaginary
(c) X(ω) and Y(ω) are both imaginary
(d) X(ω) is imaginary and Y(ω) is real
Ans: (b)
Sol: For real even function x(t), the Fourier transform X(ω) is always real even. y(t) is a derivative of x(t) which is a real odd function because derivative of even function is an odd function and hence, Fourier transform Y(ω) is imaginary odd.
Q13: A continuous-time LTI system with system function H(ω) has the following polezero plot. For this system, which of the alternatives is TRUE ? (SET-3 (2014))
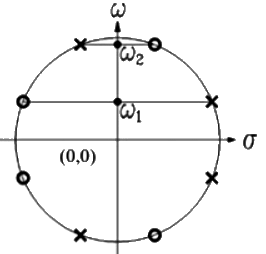 (a) ∣H(0)∣ > ∣H(ω)∣;∣ω∣ > 0
(a) ∣H(0)∣ > ∣H(ω)∣;∣ω∣ > 0
(b) ∣H(ω)∣ has multiple maxima, at ω1 and ω2
(c) ∣H(0)∣ < ∣H(ω)∣ ; ∣ω∣ > 0
(d) ∣H(ω)∣ = constant; −∞ < ω < ∞
Ans: (d)
Sol: ⇒ Symmetrically located pole and zero.
⇒ All pass filter.
⇒ Constant magnitude
(−∞ ≤ ω ≤ ∞)
Q14: A signal is represented by
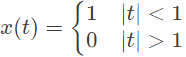 The Fourier transform of the convolved signal y(t) = x(2t) ∗ x(t/2) is (SET-3 (2014))
The Fourier transform of the convolved signal y(t) = x(2t) ∗ x(t/2) is (SET-3 (2014))
(a) 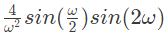
(b) 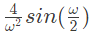
(c) 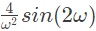
(d) 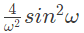
Ans: (a)
Sol: Given signal can be drawn as
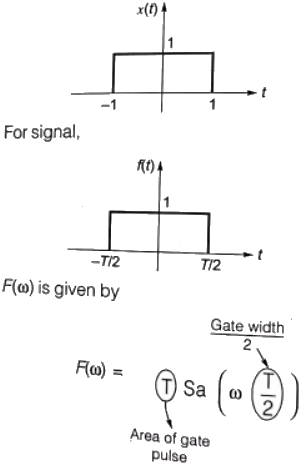 Therefore,
Therefore,
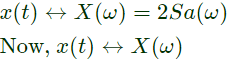 then by time scaling,
then by time scaling,
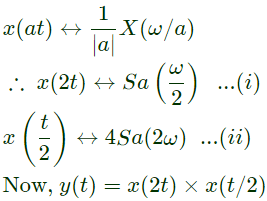 Convolution in time domain multiplication in frequency domain
Convolution in time domain multiplication in frequency domain
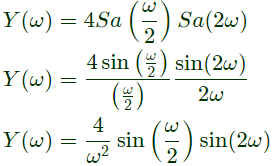
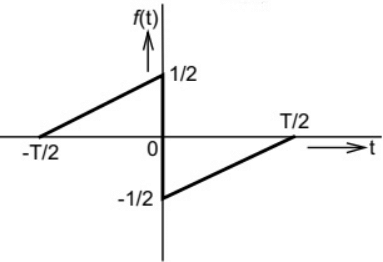
Q15: A function f(t) is shown in the figure.
 The Fourier transform F(ω) of f(t) is (SET-3 (2014))
The Fourier transform F(ω) of f(t) is (SET-3 (2014))
(a) real and even function of w
(b) real and odd function of w
(c) imaginary and odd function of w
(d) imaginary and even function of w
Ans: (c)
Sol: Fiven signal f(t) is an odd signal. Hence, F(ω) is imaginary and odd function of ω.
Q16: Let f(t) be a continuous time signal and let F(ω) be its Fourier Transform defined by 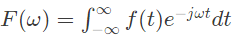
Define g(t) by 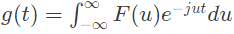
What is the relationship between f(t) and g(t) ? (SET-1 (2014))
(a) g(t) would always be proportional to f (t)
(b) g(t) would be proportional to f(t) if f(t) is an even function
(c) g(t) would be proportional to f(t) only if f(t) is a sinusoidal function
(d) g(t) would never be proportional to f(t)
Ans: (b)
Sol: Given that,
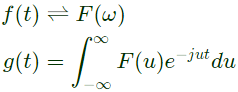
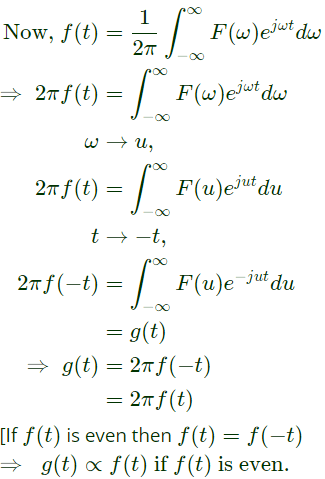
Q17: The Fourier transform of a signal h(t) is H(jω) = (2cosω)(sin2ω)/ω. The value of h(0) is (2012)
(a) 1/4
(b) 1/2
(c) 1
(d) 2
Ans: (c)
Sol: 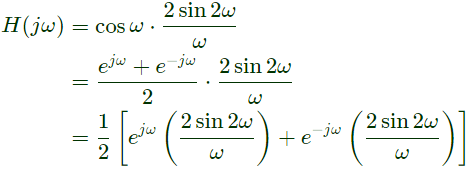
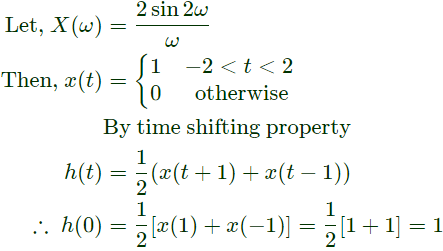
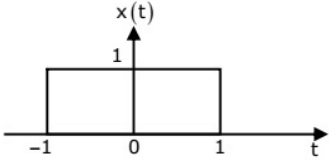
Q18: x(t) is a positive rectangular pulse from t = -1 to t = +1 with unit height as shown in the figure. The value of 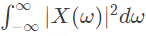 {where X(ω) is the Fourier transform of x(t)} is. (2010)
{where X(ω) is the Fourier transform of x(t)} is. (2010)
 (a) 2
(a) 2
(b) 2π
(c) 4
(d) 4π
Ans: (d)
Sol: By using Parseval's theorem,
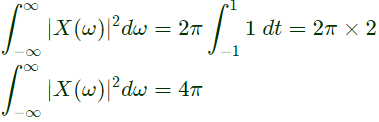
Q19: Let  and zero otherwise. Then if
and zero otherwise. Then if  the Fourier Transform of x(t)+x(−t) will be given by (2008)
the Fourier Transform of x(t)+x(−t) will be given by (2008)
(a) 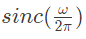
(b) 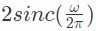
(c) 
(d) 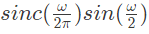
Ans: (c)
Sol: 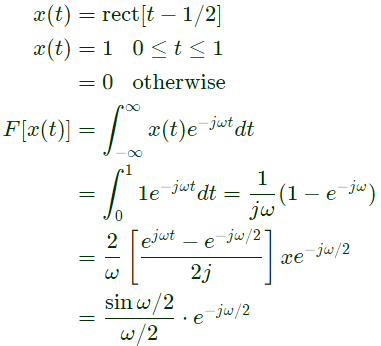
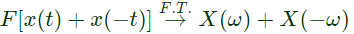
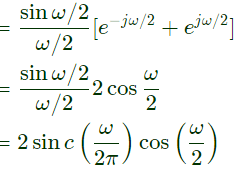
Q20: A signal x(t) = sinc(αt) where α is a real constant 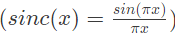 is the input to a Linear Time Invariant system whose impulse response h(t) = sinc(βt), where β is a real constant. If min (α, β) denotes the minimum of α and β and similarly, max (α, β) denotes the maximum of α and β, and K is a constant, which one of the following statements is true about the output of the system ? (2008)
is the input to a Linear Time Invariant system whose impulse response h(t) = sinc(βt), where β is a real constant. If min (α, β) denotes the minimum of α and β and similarly, max (α, β) denotes the maximum of α and β, and K is a constant, which one of the following statements is true about the output of the system ? (2008)
(a) It will be of the form Ksinc(γt) where γ = min(α, β)
(b) It will be of the form Ksinc(γt) where γ = max (α, β)
(c) It will be of the form Ksinc(αt)
(d) It can not be a sinc type of signal
Ans: (a)
Sol: 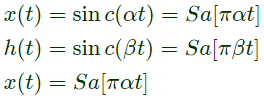
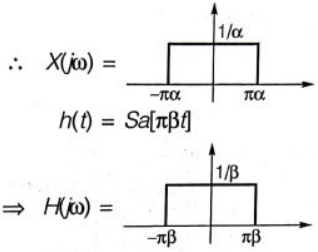
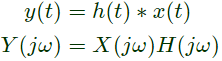
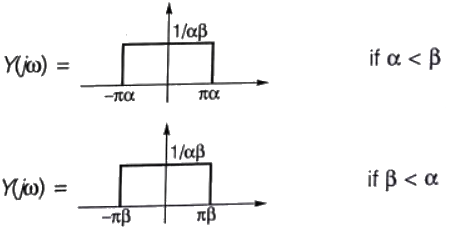
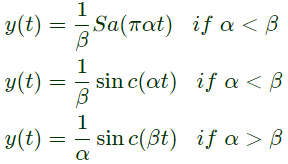 So, output is of the form k sin c(γt)
So, output is of the form k sin c(γt)
where, γ = min(α, β)
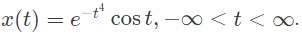 The value of the derivative of X(ω) at ω = 0 at is _____ (rounded off to 1 decimal place) (2024)
The value of the derivative of X(ω) at ω = 0 at is _____ (rounded off to 1 decimal place) (2024)
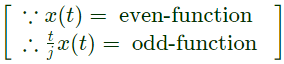
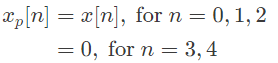 Note that
Note that 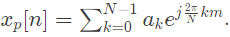 The magnitude of the Fourier series coefficient a3 is ____ (Round off to 3 decimal places). (2023)
The magnitude of the Fourier series coefficient a3 is ____ (Round off to 3 decimal places). (2023)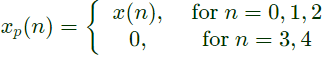
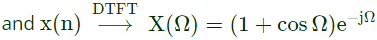 We have,
We have,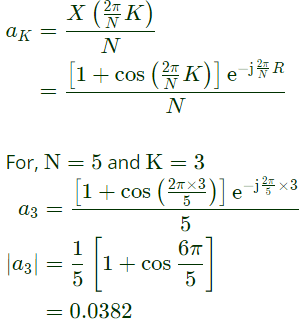
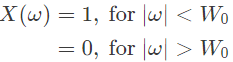 Which one of the following statements is true? (2023)
Which one of the following statements is true? (2023)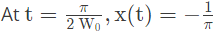 (d)
(d) 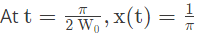 Ans: (a)
Ans: (a)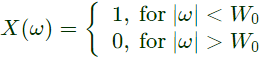
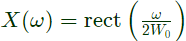
 We know,
We know,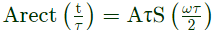 By duality,
By duality,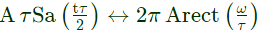 Given,
Given,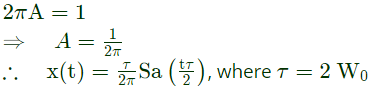 Thus,
Thus,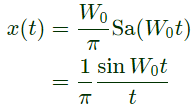
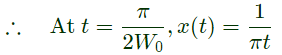 From rectangular function, At W ⇒ ∞, X(w) = 1
From rectangular function, At W ⇒ ∞, X(w) = 1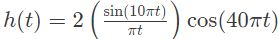 The output of the system is (2022)
The output of the system is (2022)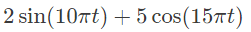
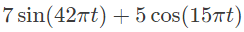
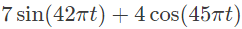
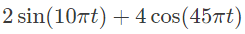
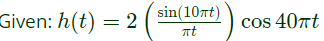 Fourier transform of signal
Fourier transform of signal 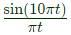 is given by
is given by Now, impulse response
Now, impulse response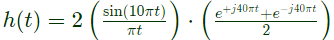 Using property,
Using property, 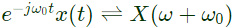
 Cut-off frequencies,
Cut-off frequencies,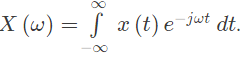 The maximum magnitude of X(ω) is _____. (2021)
The maximum magnitude of X(ω) is _____. (2021)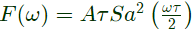
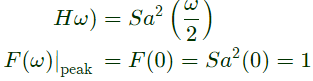 ∵ Peak value of sampling function occurs at ω = 0
∵ Peak value of sampling function occurs at ω = 0 
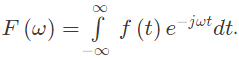 Suppose
Suppose 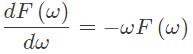 for all ω, and F(0) = 1. Then (2021)
for all ω, and F(0) = 1. Then (2021)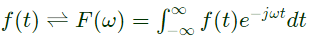 The following informations are given about
The following informations are given about 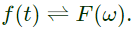
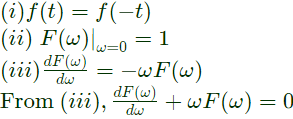 By solving the above linear differential equations, (by mathematics)
By solving the above linear differential equations, (by mathematics)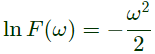 ⇒
⇒ 

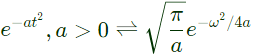
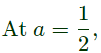
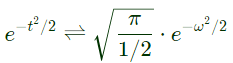
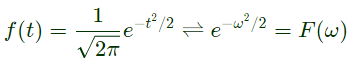 Thus,
Thus, 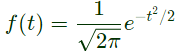
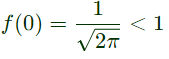
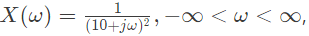
 and ω denotes frequency. Then the value of |lnx(t)| at t = 1 is ___________ (up to 1 decimal place). ( ln denotes the logarithm to base e) (2018)
and ω denotes frequency. Then the value of |lnx(t)| at t = 1 is ___________ (up to 1 decimal place). ( ln denotes the logarithm to base e) (2018)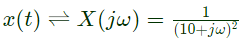 By taking inverse Fourier transform,
By taking inverse Fourier transform,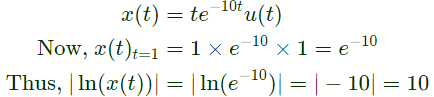
 is equal to (SET-2 (2016))
is equal to (SET-2 (2016))
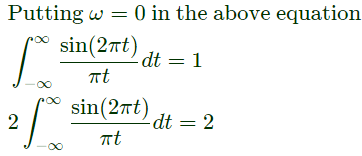
 Which one of the following statements is TRUE? (SET-1 (2016))
Which one of the following statements is TRUE? (SET-1 (2016))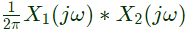 and by looking at X1(jω) and X2(jω), we can say that X1(jω)∗X2(jω) will be conjugate symmetric and thus x1(t)⋅x2(t) will be real.
and by looking at X1(jω) and X2(jω), we can say that X1(jω)∗X2(jω) will be conjugate symmetric and thus x1(t)⋅x2(t) will be real.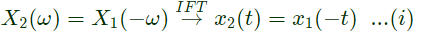 Now, X1(jω) is real. Therefore, x1(t) will be conjugate symmetric.
Now, X1(jω) is real. Therefore, x1(t) will be conjugate symmetric. 

 Its Fourier Transform is (SET-2 (2015))
Its Fourier Transform is (SET-2 (2015))
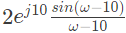
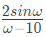
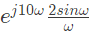
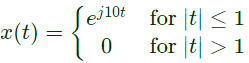
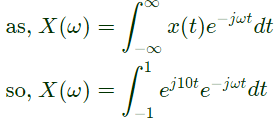
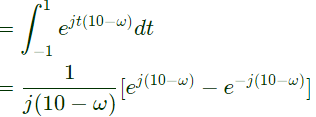
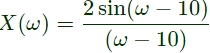
 (a) ∣H(0)∣ > ∣H(ω)∣;∣ω∣ > 0
(a) ∣H(0)∣ > ∣H(ω)∣;∣ω∣ > 0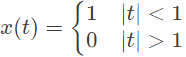 The Fourier transform of the convolved signal y(t) = x(2t) ∗ x(t/2) is (SET-3 (2014))
The Fourier transform of the convolved signal y(t) = x(2t) ∗ x(t/2) is (SET-3 (2014))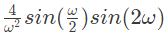
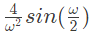
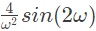
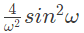
 Therefore,
Therefore,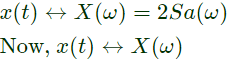 then by time scaling,
then by time scaling,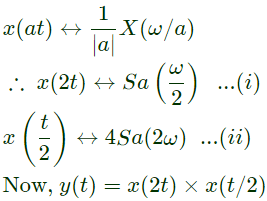 Convolution in time domain multiplication in frequency domain
Convolution in time domain multiplication in frequency domain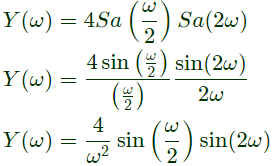
 The Fourier transform F(ω) of f(t) is (SET-3 (2014))
The Fourier transform F(ω) of f(t) is (SET-3 (2014))
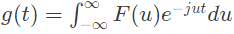
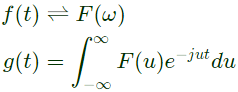
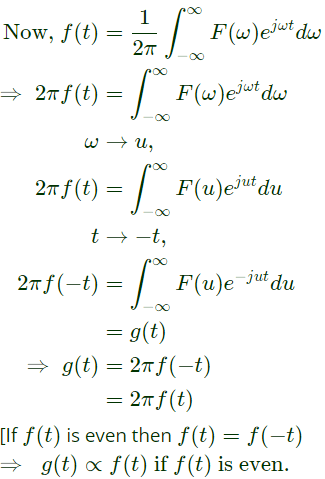
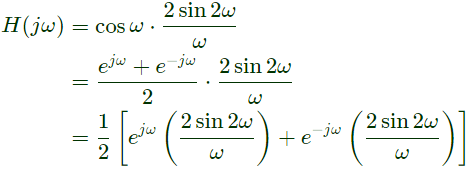
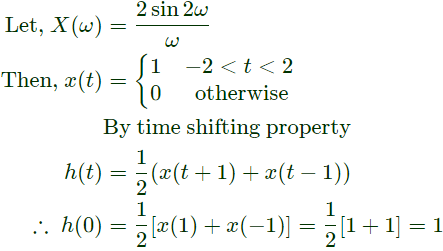
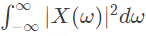 {where X(ω) is the Fourier transform of x(t)} is. (2010)
{where X(ω) is the Fourier transform of x(t)} is. (2010) (a) 2
(a) 2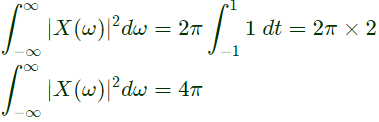
 and zero otherwise. Then if
and zero otherwise. Then if  the Fourier Transform of x(t)+x(−t) will be given by (2008)
the Fourier Transform of x(t)+x(−t) will be given by (2008)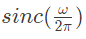
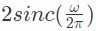

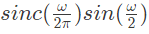
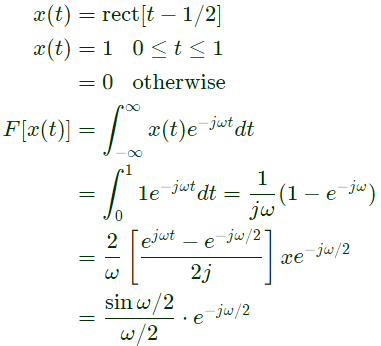
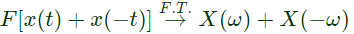
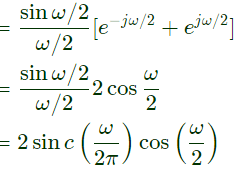
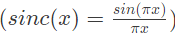 is the input to a Linear Time Invariant system whose impulse response h(t) = sinc(βt), where β is a real constant. If min (α, β) denotes the minimum of α and β and similarly, max (α, β) denotes the maximum of α and β, and K is a constant, which one of the following statements is true about the output of the system ? (2008)
is the input to a Linear Time Invariant system whose impulse response h(t) = sinc(βt), where β is a real constant. If min (α, β) denotes the minimum of α and β and similarly, max (α, β) denotes the maximum of α and β, and K is a constant, which one of the following statements is true about the output of the system ? (2008)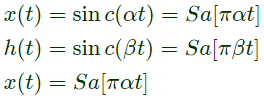

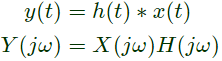

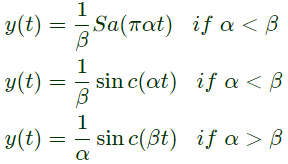 So, output is of the form k sin c(γt)
So, output is of the form k sin c(γt)

























