ANOVA & Chi-square Test | Crash Course for UGC NET Commerce PDF Download
| Table of contents |

|
| Using ANOVA |

|
| History of ANOVA |

|
| What ANOVA Reveals |

|
| Chi-Square Distribution |

|
| Chi-Square Test of Independence |

|
Using ANOVA

ANOVA (Analysis of Variance) is a statistical test designed to compare the means of multiple groups at once. It helps determine whether the observed differences in group means are due to random chance or represent meaningful distinctions. Essentially, ANOVA allows for the simultaneous comparison of means across various groups, making it a powerful tool in data analysis.
In a one-way ANOVA, there is one independent variable, while a two-way ANOVA involves two independent variables. This test is often used in regression studies to understand the impact of independent variables on a dependent variable. Though the concept may seem complex at first, ANOVA has far-reaching applications, from evaluating new medical treatments to assessing consumer preferences in marketing. It has become a crucial tool for analyzing complex systems and enabling data-driven decision-making.
Key Points:
- ANOVA is a statistical technique that compares means across multiple groups to determine if differences are significant or due to chance.
- A one-way ANOVA involves a single independent variable, while a two-way ANOVA includes two independent variables.
- ANOVA partitions total variance into components, helping to uncover relationships between variables and pinpoint real sources of variation.
- It can handle multiple factors and their interactions, making it a versatile and powerful method for understanding complex relationships.
Applications of ANOVA
ANOVA is particularly useful in experimental data analysis. When statistical software isn't available, it can be calculated manually and is especially well-suited for small sample sizes, whether comparing groups, subjects, or experimental conditions.
ANOVA operates similarly to several two-sample t-tests but reduces the likelihood of type I errors. It compares group differences by examining the means and partitioning the variance into different sources. A one-way ANOVA looks at the relationship between one independent variable and a dependent variable, while a two-way ANOVA handles two independent variables. The independent variable must have at least three groups or categories, and the test assesses whether the dependent variable changes with the independent variable.
For example, researchers might use ANOVA to compare the performance of students from different colleges to see if any consistently outperform the others. In a business context, it could be used to test two methods of production to determine which is more cost-efficient.
Thanks to its flexibility and ability to analyze multiple variables at once, ANOVA is invaluable for researchers and analysts in a variety of fields. By comparing means and breaking down variance, it helps uncover significant differences and deeper relationships among variables.
ANOVA Formula
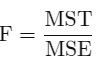
where:
F = ANOVA coefficient
MST = Mean sum of squares due to treatment
MSE = Mean sum of squares due to error
History of ANOVA
In the early 20th century, statistical analysis relied on methods like the t-test and z-test. In 1918, Ronald Fisher introduced the analysis of variance (ANOVA) method, which marked a significant advancement in the field. ANOVA, often referred to as Fisher's analysis of variance, is an extension of these earlier tests. The term gained wider recognition in 1925 with the publication of Fisher's book, Statistical Methods for Research Workers. Initially used in experimental psychology, ANOVA soon spread to other disciplines.
ANOVA serves as a foundational step in analyzing the factors that influence a data set. After conducting the test, analysts can further investigate the factors that may contribute to any observed inconsistencies in the data. The results of the ANOVA test are often used in an F-test, which helps generate additional data to refine regression models.
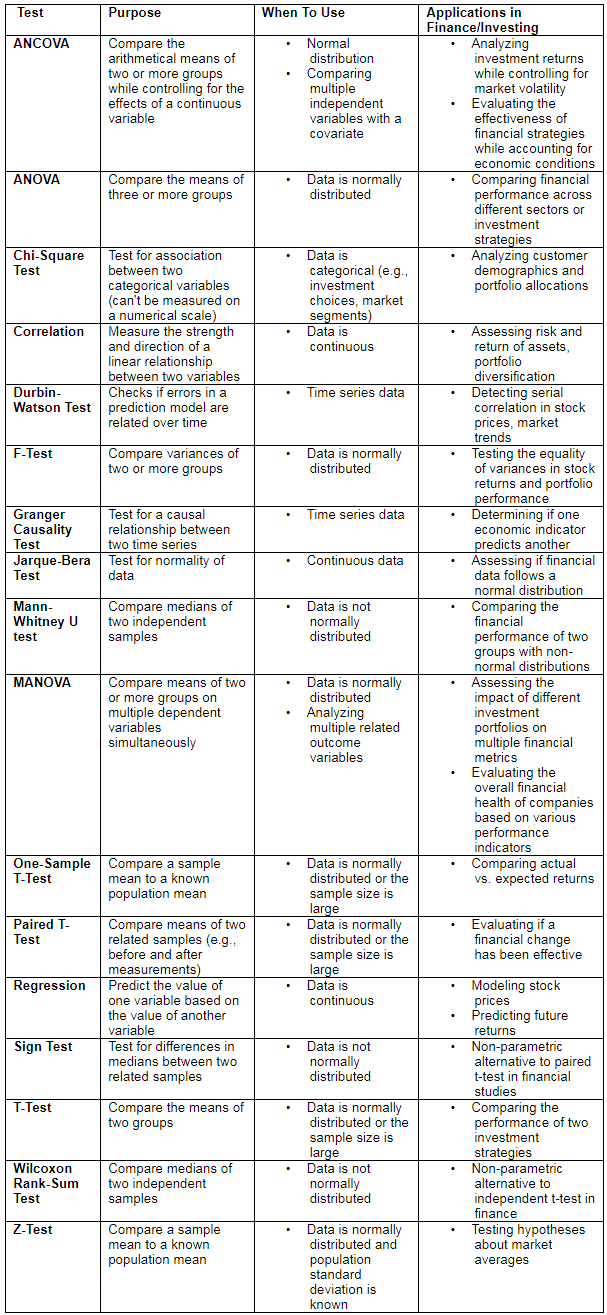
Cheat Sheet on Common Statistical Tests in Finance and Investing
What ANOVA Reveals
ANOVA breaks down the overall variability in a dataset into two components: systematic factors and random factors. Systematic factors have an influence on the dataset, while random factors do not. By using ANOVA, researchers can compare multiple groups simultaneously to determine if there is a relationship between them. The test produces an F-statistic (or F-ratio) that allows for the analysis of variability both between and within data groups.
When no significant difference exists between the groups (the null hypothesis), the F-ratio will be close to one. The distribution of possible F-statistic values is known as the F-distribution, which is characterized by two parameters: the numerator degrees of freedom and the denominator degrees of freedom.
One-Way vs. Two-Way ANOVA
One-Way ANOVA: Uses a single independent variable or factor to evaluate its impact on a continuous dependent variable. It assesses significant differences among group means but does not account for interactions between variables.
Two-Way ANOVA: Involves two independent variables and examines both their individual effects and how their interaction influences the outcome. This allows for the testing of interactions between the variables, offering deeper insights.
A one-way ANOVA determines whether the means of three or more independent groups are statistically different. A two-way ANOVA, on the other hand, explores the influence of two independent variables on a dependent variable. For example, a company could use a two-way ANOVA to compare worker productivity based on salary and skill set. It also assesses interactions between the two factors to understand their combined effect.
ANOVA Example
Imagine you want to evaluate how different investment portfolios perform under varying market conditions. You have three portfolio strategies:
- Technology portfolio (high-risk, high return)
- Balanced portfolio (moderate-risk, moderate return)
- Fixed-income portfolio (low-risk, low return)
You also consider two market conditions:
- Bull market
- Bear market
One-Way ANOVA: This could be used to analyze the performance differences among the three portfolios without considering market conditions. The independent variable is the type of portfolio, and the dependent variable is the returns. You compare the mean returns of the three portfolios over a set period to determine if the differences are statistically significant.
Two-Way ANOVA: This method would analyze the effects of both the portfolio type and the market conditions on returns, including interactions between these two factors. You would group the returns of each portfolio under both bull and bear market conditions and compare the mean returns. This analysis reveals not only the impact of each factor but also how their interaction affects returns.
For example, a technology portfolio may perform better in bull markets but underperform in bear markets, while a fixed-income portfolio may deliver stable returns in both. This helps determine the best strategies for different market conditions.
How ANOVA Differs From a T-Test
ANOVA can compare three or more groups, while t-tests are limited to comparing only two groups at a time.
What Is Analysis of Covariance (ANCOVA)?
ANCOVA combines ANOVA and regression, allowing for the exploration of within-group variance that ANOVA alone cannot explain.
Does ANOVA Have Assumptions?
Yes, ANOVA assumes that the data is normally distributed, that group variances are roughly equal, and that all observations are made independently. If these assumptions are violated, ANOVA may not provide accurate comparisons.
Chi-Square Distribution
When the null hypothesis is assumed to be true, the sampling distribution of the test statistic follows a chi-squared distribution. The chi-square test is a statistical method used to determine if there is a significant difference between the expected and observed frequencies across one or more categories. It helps assess the probability of the relationship between independent variables.
Note: The chi-square test is applicable only to categorical data, such as gender (e.g., male and female), age groups, or height categories.
Finding P-Value
The "P" in p-value stands for probability. The chi-square test is used to calculate the p-value in statistics. The p-value helps interpret the hypothesis test outcome:
- P ≤ 0.05: Reject the null hypothesis
- P > 0.05: Accept the null hypothesis
Probability reflects the likelihood or risk of a particular outcome. In statistics, it relates to how we manage and interpret data, allowing for the simplification and presentation of large, complex datasets. Both probability and statistics are integral to the chi-square test.
Properties
Key properties of the chi-square test include:
- The variance is twice the number of degrees of freedom.
- The mean of the distribution is equal to the number of degrees of freedom.
- As the degrees of freedom increase, the chi-square distribution approaches a normal distribution.
Formula
The chi-square test compares the observed values with expected values to determine whether differences exist. The formula for chi-square is given as:

or
X2 = ∑(Oi – Ei)2/Ei
where Oi is the observed value and Ei is the expected value.
Chi-Square Test of Independence
The chi-square test of independence (also called the chi-square test of association) is used to assess whether there is an association between two categorical variables. It is a non-parametric test, commonly applied to test for statistical independence.
This test is not suitable when the categorical variables represent pre-test and post-test observations. For valid results, the data must meet the following conditions:
- Two categorical variables
- A relatively large sample size
- Variables must have two or more categories
- Independence of observations
Example of Categorical Data
Consider a society of 1,000 residents, divided into four neighborhoods: P, Q, R, and S. A random sample of 650 residents, categorized by profession (doctors, engineers, and teachers), is taken. The null hypothesis assumes that residency is independent of professional division.
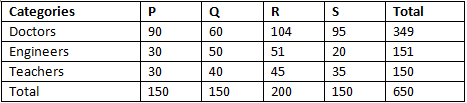
For example, in neighborhood P, there are 150 residents, and the sample has 349 doctors. The expected number of doctors in neighborhood P would be calculated as:
Suppose there are 150 people living in neighborhood P, and we want to estimate what proportion of the entire 1,000 residents live in this neighborhood. Similarly, 349 out of 650 people in the sample are doctors. Based on the assumption of independence under the null hypothesis, we calculate the expected number of doctors living in neighborhood P as:
Using the chi-square test formula for this cell, we compute the chi-square statistic as: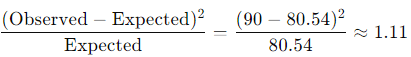
Key Facts About the Chi-Square Test
- The chi-square test is performed on raw numerical data, not on percentages, proportions, means, or similar statistical measures. For example, if we have 20% of 400 people, we must convert it to a number (i.e., 80) before calculating the test statistic.
- The chi-square test yields a p-value, which helps determine whether the test results are statistically significant.
To perform a chi-square test and obtain the p-value, two pieces of information are essential:
- Degrees of Freedom (DF): This is the number of categories minus 1.
- Alpha Level (α): This threshold is chosen by the researcher, with a common alpha level being 0.05 (5%), although other levels like 0.01 or 0.10 may also be used.
In introductory statistics, problems often provide the degrees of freedom and alpha level, so there's usually no need to calculate them. To determine the degrees of freedom, count the number of categories and subtract 1.
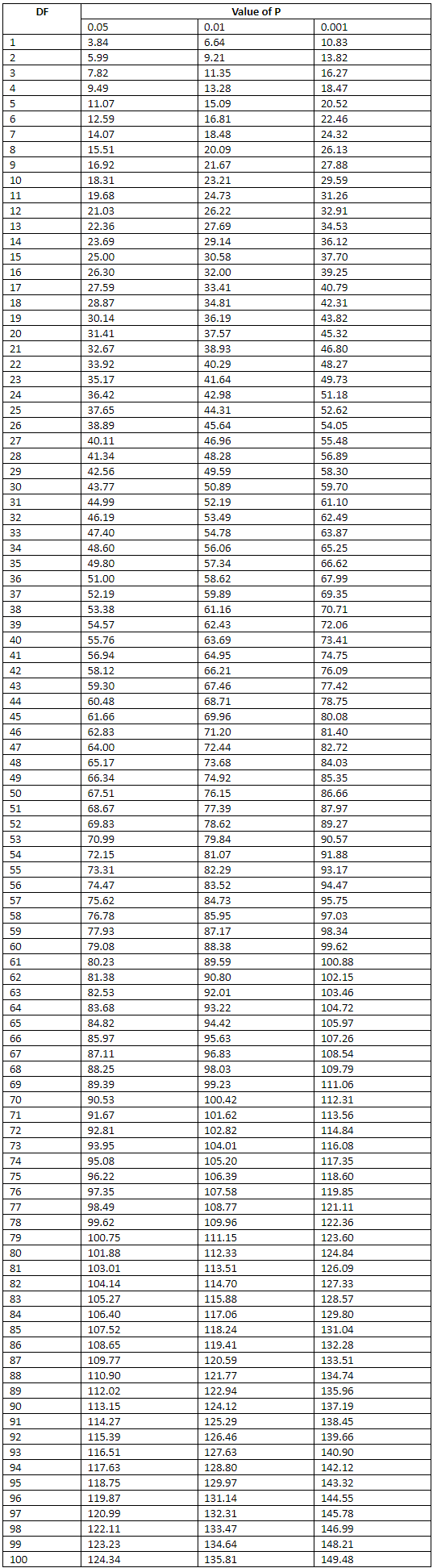
Chi-Square Distribution Table
The chi-square distribution table, provided with three probability levels, is used to assess whether the distributions of specific variables differ from each other. Categorical variables yield data in discrete categories, while numerical variables yield data in numerical form.
The chi-square distribution with degrees of freedom (r−1)(c−1) is represented in this table, where r is the number of rows in a two-way table and c is the number of columns.
|
157 videos|236 docs|166 tests
|
FAQs on ANOVA & Chi-square Test - Crash Course for UGC NET Commerce
| 1. What is the history of ANOVA? |  |
| 2. What does ANOVA reveal? |  |
| 3. What is the Chi-Square distribution used for? |  |
| 4. How does the Chi-Square test of independence differ from ANOVA? |  |
| 5. How does UGC NET relate to ANOVA and Chi-Square tests? |  |




















