Fractions Chapter Notes | Mathematics for Class 6 PDF Download
Introduction
A fraction is a way to represent a part of a whole.
Think of a pizza cut into two equal slices. If you divide the pizza into two equal slices, each child's share will be .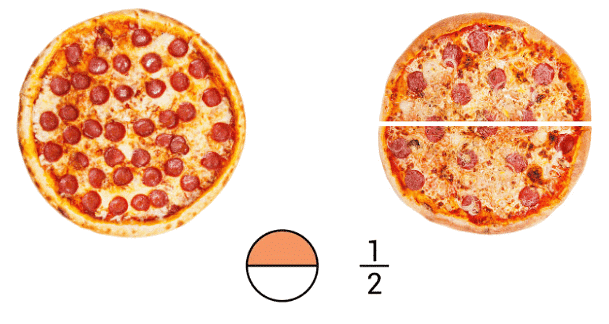
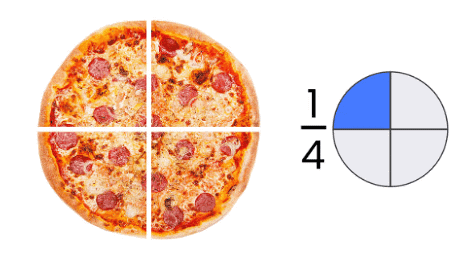
Now, if you divide the pizza into four equal slices, each child's share will be, .
 Fractions help us explain and understand situations where something is split into equal parts.
Fractions help us explain and understand situations where something is split into equal parts.
Let us understand this concept better.
A Fraction
A fraction means a part of a group or of a region.
When we look at a fraction, it has two important numbers:
Numerator (Top Number):
- This tells us how many parts of the whole we have or are using.
- For example, in the fraction
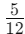 , the numerator is 5, meaning we have 5 parts out of the total.
, the numerator is 5, meaning we have 5 parts out of the total.
Denominator (Bottom Number):
- This tells us into how many equal parts the whole is divided.
- In
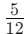 , the denominator is 12, meaning the whole is divided into 12 equal parts.
, the denominator is 12, meaning the whole is divided into 12 equal parts.

Let us understand fractions with the help of an example:
Ethan is celebrating his birthday at home. His mother has baked a cake for his birthday. When his friends came home, he cut the cake.
His mother wants to distribute the cake equally among all his friends.
There are six people (including Ethan’s mother) at the party.
So, his mother cuts the cake into 6 equal parts.
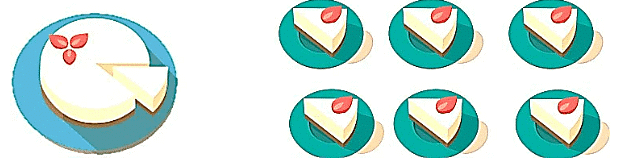 Fractions of a Cake
Fractions of a Cake
Can you tell what fraction of the cake Ethan gets?
Total number of slices of cake = 6
Ethan got (one-sixth) part of the cake.
So, Ethan ate one part out of six parts of the cake.
Here 1 is the numerator and 6 is the denominator.
Fractional Units and Equal Shares
A fractional unit refers to a part of a whole that has been divided into equal sections. When we split something into equal parts, each part is known as a fractional unit.
Understanding with Example

Consider a chocolate bar that you wish to share with your friends. Suppose you have 1 chocolate bar and 4 friends, including yourself, meaning you need to divide the chocolate into 4 equal pieces.
- Each piece you receive is a fractional unit of the entire chocolate bar. In this case, as the chocolate is split into 4 equal parts, each piece is 1/4 of the chocolate bar.




- Now, let’s examine a different scenario. You still have 1 chocolate bar, but this time you need to share it with 9 friends.
- If you share the chocolate bar into 9 equal parts, each piece will be 1/9 of the chocolate bar.
Comparison: Which piece is larger, 1/4 or 1/9? When you divide the chocolate into 4 parts, each piece is more significant because fewer people are sharing it. Thus, 1/4 is larger than 1/9.
This example illustrates that as the number of parts increases, each fractional unit (or piece) becomes smaller.
Knowledge from the Past: The History of Fractions in India
- Fractions have a rich history in India, originating from ancient times when they were acknowledged and named in various texts.
- In the Rig Veda, one of the oldest texts in Indian literature, fractions were referred to as "tripada."
- This indicates that the terms for fractions used in modern Indian languages have roots in ancient history.
- Overall, the current understanding and naming of fractions in India have a profound historical background.

Fractional Units as Parts of a Whole
A fractional unit is a single part of something that has been split into equal pieces. When a whole is divided into equal parts, each part is known as a fractional unit of that whole.
Imagine a traditional sweet called "chikki", which is a rectangular bar made from jaggery and nuts. Let’s say you have one whole chikki and want to split it into equal parts.
Dividing the Chikki into 2 Parts:

- If you break the chikki into 2 equal pieces, each piece is 1/2 of the whole chikki.
- Here, the fractional unit is 1/2, meaning each piece represents half of the original chikki.
Dividing the Chikki into 6 Parts:
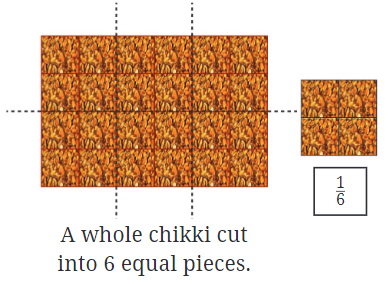
- If you take the same chikki and break it into 6 equal pieces, each piece is 1/6 of the whole chikki.
- Here, the fractional unit is 1/6, meaning each piece is one-sixth of the original chikki.
Understanding Different Shapes: Sometimes, even if the pieces look different, they can still be the same size. For instance, if you cut the chikki into 6 equal pieces, each piece might appear different based on the cut, but each one remains 1/6 of the whole chikki.
Proper and Improper Fractions:
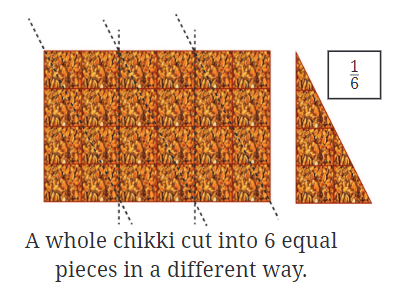
The fractions we discussed earlier, like 1/2 and 1/6, are known as proper fractions. In contrast, improper fractions occur when the numerator is greater than or equal to the denominator, such as 5/4 or 3/2.
Multiplying Whole Numbers with Fractions:
To multiply a whole number by a proper or improper fraction, multiply the whole number by the numerator of the fraction and then divide by the denominator. For example, if Farida has 20 marbles and Reshma has 1/5 of that number, we can find out how many marbles Reshma has:
Reshma has 1/5 × 20 = 4 marbles.
Measuring Using Fractional Units
Measuring using fractional units involves dividing a whole object or quantity into smaller, equal parts to make measurement easier. When something is too big to measure in its entirety, we can split it into fractions, which are smaller, equal sections. This approach helps us describe and understand how much of something we have, even when it's not a complete whole.
Understanding with an Example
Imagine you have a strip of paper that is one unit long. If you fold this strip into two equal parts, each part is now 1/2 (one-half) of the original strip. If you fold it again into four equal parts, each part becomes 1/4 (one-quarter) of the original strip.

Now, consider a whole roti (a round flatbread). If you cut the roti into two equal parts, each part is 1/2 of the whole roti. If you cut it into four equal parts, each part is 1/4 of the whole roti.
This method of using fractional units like 1/2, 1/4, and so on helps us measure and describe parts of a whole.
Reading Fractions
- Fractions can be read in different ways. For example, the fraction 3/4 can be read as "three quarters" or "three upon four." However, reading it as "three times one-fourth" makes it easier to understand the size of the fraction. This way, we see what the fractional unit is (1/4) and how many of these units there are(3).
- In a fraction, the top number is the numerator, and the bottom number is the denominator. For example, in the fraction 5/6, 5 is the numerator, and 6 is the denominator.
Practical Applications of Fractions
Fractions are used in many everyday situations. For example:
- When cooking, recipes may require ingredients in fractional amounts, such as 1/2 cup of sugar or 3/4 teaspoon of salt.
- Fractions are also important in measuring distances, like when a carpenter measures a piece of wood to be cut into 1/3 of its length.
Understanding fractions allows us to make accurate measurements and calculations in daily tasks.
Marking Fraction Lengths on the Number Line
Representing fractions on a number line means that we can plot fractions on a number line, which is similar to plotting whole numbers and integers. Fractions represent parts of a whole.
So, fractions on the number line are represented by making equal parts of a whole i.e. 0 to 1, and the number of those equal parts would be the same as the number written in the denominator of the fraction. For example, to represent 1/8 on the number line, we have to divide 0 to 1 into 8 equal parts and mark the first part as 1/8.
1. Understand the Number Line Basics:
- A number line is a straight line where numbers are placed at equal distances.
- Whole numbers like 0, 1, 2, etc., are marked on this line.
2. Identify the Fraction to Show:
- For example, you want to show the fraction 3/7.
- This fraction means you have 3 parts out of 7 equal parts.
3. Divide the Length Between 0 and 1:
- Since the denominator is 7, divide the length between 0 and 1 into 7 equal parts.
4. Mark the Fraction:
- Count 3 parts from 0. The point where you stop is 3/7 on the number line.
- Mark this point as "P" to show 3/7.
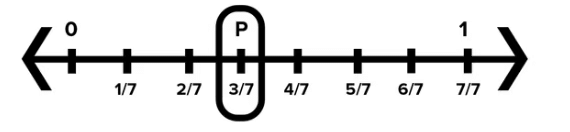
5. Mark Other Related Fractions:
- /7: This is simply 0, so mark it at the starting point of the line.
- /7: Since is equal to 1, mark it at the point where 1 is on the number line.
Examples:
- Consider a fraction 1/2.
1/2 is greater than 0, but less than 1.
Divide the space between 0 and 1 into two equal parts. We can show one part as the fraction 1/2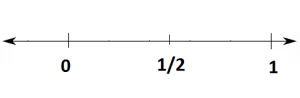
- Consider another 1/5.
1/5 fraction is greater than 0, but less than 1.
Divide the space between 0 and 1 into five equal parts. We can show the first part as 1/5 the second as 2/5 the third as 3/5 the fourth as 4/5 and the fifth part as 5/5=1.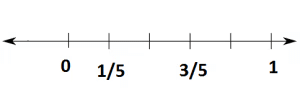
Understanding Improper Fractions
- A fraction where the numerator (the top number) is larger than the denominator (the bottom number). This means the fraction represents a quantity greater than or equal to 1.
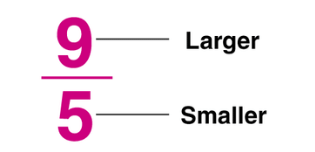
- 9/5 is an improper fraction as it means 9 parts are being divided into groups of 5. It means you have 9 parts, and each part is one-fifth of a whole. Since 9 is more than 5, this fraction is greater than 1.
- To understand 9/5, you can think of it as dividing 9 by 5. When you do this division, the result is 1 whole (5/5) with 4 parts remaining.
So, 9/5 can be written as: 1 (whole) + 4/ 5 (parts left over)
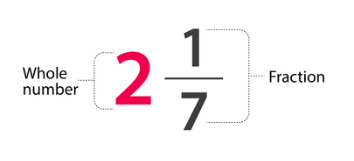
Mixed Fractions
A mixed fraction combines a whole number with a proper fraction. It shows how many whole parts there are, along with a fraction of another part.
- For example, if you have 1 whole pizza and an additional half, it can be written as a mixed fraction: 1 1/2. This means you have 1 whole pizza plus another 1/2 pizza.

Writing Fractions Greater Than One as Mixed Numbers
Understanding Mixed Numbers
When we encounter a fraction that is more than one, we can express it as a mixed number. A mixed number combines a whole number with a fraction, which helps to illustrate how many whole parts we have and what fraction remains.
Improper Fractions Explained
1. Conversion of improper fraction into mixed fraction
An improper fraction can be expressed as mixed fraction by dividing the numerator by the denominator of the improper fraction to obtain the quotient and the remainder.
Divide the Numerator by the Denominator:
- The numerator is the number on top, and the denominator is the number on the bottom of the fraction.
- Perform the division to get a quotient (the whole number part) and a remainder (the part left over).
Form the Mixed Fraction:
The quotient becomes the whole number part of the mixed fraction.
The remainder becomes the new numerator of the fraction, and the denominator remains the same.
The mixed fraction is then written as:
Then the mixed fraction will be.
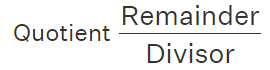
Example: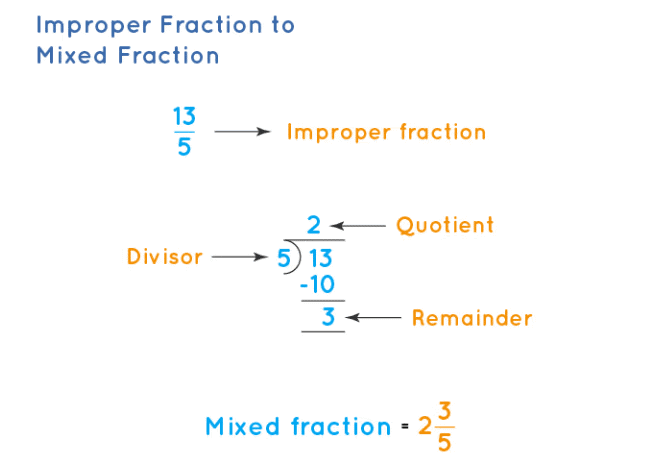
2. Conversion of mixed fraction into an improper fraction:
Multiply the Whole Number by the Denominator:
- Start by taking the whole number part of the mixed fraction and multiplying it by the denominator (the bottom number of the fraction).
Add the Numerator to the Product:
- After multiplying, add the numerator (the top number of the fraction) to the product from the first step.
Form the Improper Fraction:
- The sum from step 2 becomes the numerator of the improper fraction.
The denominator remains the same as in the original fraction.
Let us convert this mixed fraction to an improper fraction using the following steps and the explanation given below.
- Step 1: Multiply the denominator of the mixed fraction with the whole number part. In this case, 5 × 2 = 10
- Step 2: Add the numerator to the product obtained from Step 1. Here, 4 + 10 = 14.
- Step 3: Write the improper fraction with the sum obtained from Step 2 in the numerator/denominator form. Here, it will be 14/5.

Equivalent Fractions
These are fractions that represent the same value or part of a whole, even though they have different numerators and denominators.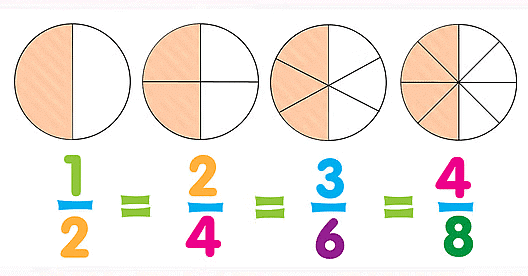
Using a fraction wall to find equal fractional lengths!
Equivalent fractions are different fractions that represent the same amount. To see if fractions like 1/2 and 2/4 are equal, we can use strips of paper.
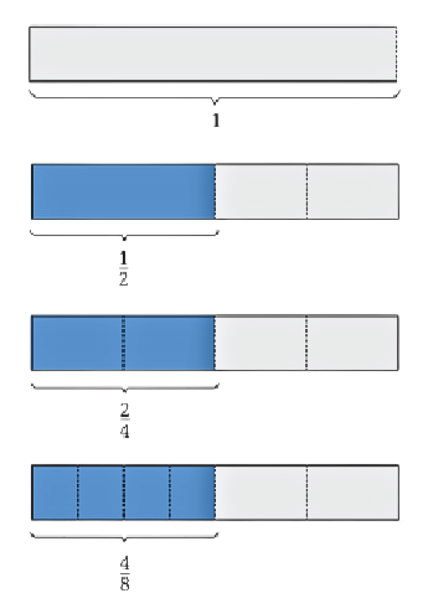 1/2, 2/4 and 4/8 are equivalent fractions, as shown using paper strips. You can create a fraction wall to help compare and visualize different fractions more effectively.
1/2, 2/4 and 4/8 are equivalent fractions, as shown using paper strips. You can create a fraction wall to help compare and visualize different fractions more effectively.
Understanding Equivalent Fractions using Equal Shares
Understanding with an Example
When a roti is shared equally among four children, each child gets a part of the whole roti. The diagram shows how the roti is cut into four equal parts.
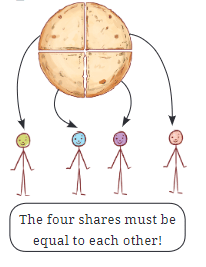
Each child's portion of the roti is 1/4. This demonstrates equivalent fractions, as the shares can also be shown in other forms. For instance, the reciprocal of a fraction is found by swapping the top and bottom numbers. So, the reciprocal of 1/4 is 4/1.
Also, we can use fractions to describe the area of a rectangle. For example, if the length is 3/4 and the width is 1/2, the area can be figured out as:
- Area: Length x Width = 3/4 x 1/2 = 3/8 square units.
How to Find Equivalent Fractions
Multiplying Both Numerator and Denominator: To find an equivalent fraction, multiply both the numerator (top number) and the denominator (bottom number) by the same number.
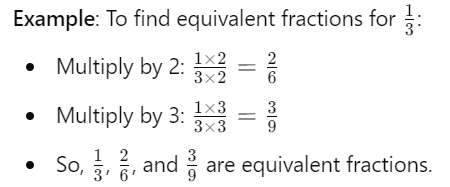
Dividing Both Numerator and Denominator: Alternatively, you can divide both the numerator and the denominator by the same number to find equivalent fractions.
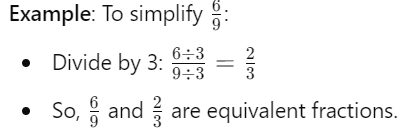
Equivalent fractions represent the same part of a whole because they are different ways of expressing the same proportion. When you multiply or divide the numerator and denominator by the same number, you are essentially scaling the fraction but keeping the same overall value.
Expressing a Fraction in Lowest Terms (or in its Simplest Form)
Understanding Lowest Terms
A fraction is in its lowest terms or simplest form when the top number (numerator) and the bottom number (denominator) share no common factors apart from 1. This means both numbers are as small as they can be and the fraction cannot be reduced any further.
- To put a fraction in lowest terms, divide both the numerator and denominator by their greatest common factor (GCF).
Important Note: The greatest common divisor (GCD) is key to simplifying fractions, as it helps find the largest number that can evenly divide both the numerator and the denominator.
Step-by-Step Example: Simplifying 36/60
- Step 1: Both 36 and 60 are even, so divide by 2:

- Step 2: Now, 18 and 30 are also even, so divide by 2 again:
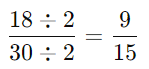
- Step 3: Next, 9 and 15 are multiples of 3, so divide both by 3:
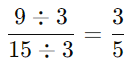
- Now, 3/5 is in its simplest form since 3 and 5 have no common factors other than 1.
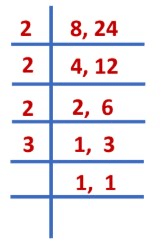
Example: Find the simplest form of the fraction 11/33
Comparing Fractions
1. Comparing Like Fractions
Comparing fractions involves figuring out which of two or more fractions is larger or smaller. A simple way to do this is by turning them into equivalent fractions that have the same denominator. When the fractions share a denominator, we can directly compare the numerators (the top numbers) to establish which fraction is greater.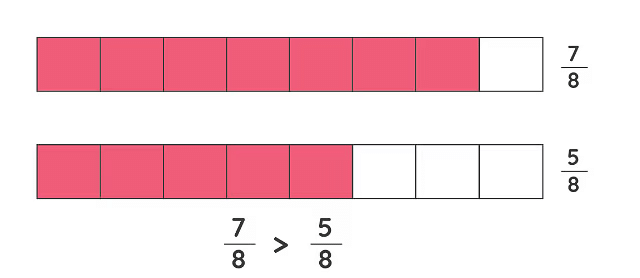
It's also useful to know about reciprocals when dealing with fractions. The reciprocal of a fraction is found by flipping its numerator and denominator.
Here's how to compare the fractions 4/9 and 5/7:
- Step 1: Identify a common denominator. This is a number that both denominators (9 and 7) can divide into. Here, the common denominator is 63.
- Step 2: Adjust each fraction to match the common denominator:
- 4/9 changes to 28/63 since 4 × 7 = 28 and 9 × 7 = 63.
- 5/7 changes to 45/63 since 5 × 9 = 45 and 7 × 9 = 63.
- Step 3: Now, compare the numerators (28 and 45):
- Since 45 > 28, it shows that 5/7 is greater than 4/9.
2. Comparing Unlike Fractions
- If two fractions with the same numerator but different denominators are to be compared, then the fraction with the smaller denominator is the greater of the two.
- To compare fractions with unlike denominators, we have to convert them to like denominators for which we have to find the Least Common Multiple (LCM) of the denominators. As the denominators are made equal, we can compare the fractions with ease.
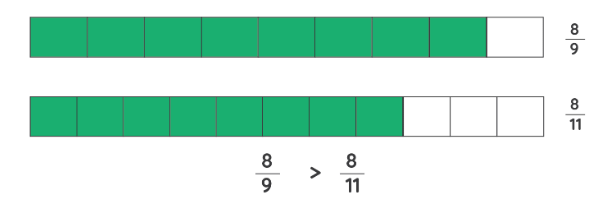 Comparing Unlike Fractions
Comparing Unlike Fractions
Example: Compare: 1/4 and 2/3.
Step 1: First, observe the denominators of the given fractions, i.e., 1/4 and 2/3. Since the denominators are different make them equal by finding the LCM of 4 and 3. LCM(4,3) = 12.
Step 2: Now, let us convert the given fraction in such a way that they have the same denominators. So, multiply the first fraction with 3/3, i.e., 1/4 × 3/3 = 3/12.
Step 3: Similarly, multiply the second fraction with 4/4, i.e., 2/3 × 4/4 = 8/12. Thus, the first fraction becomes 3/12 and the other becomes 8/12.
Step 4: Compare the obtained new fractions, i.e., 3/12 and 8/12. As the denominators are the same, we will compare the numerators. We can observe that 3 < 8.
Step 5: The fraction that has a large numerator is the larger fraction. So, 8/12 > 3/12. So, 2/3 > 1/4.
Addition and Subtraction of Fractions
Addition and Subtraction of Fractions mean putting together or taking away parts of a whole. To add or subtract fractions, they need to have the same bottom number (denominator). If they don't, you must find a common denominator first. This is usually the lowest common multiple (LCM) of the denominators.
1. Addition and Subtraction of fractions with same denominator:
When we add or subtract like fractions, we add or subtract their numerators and the denominator remains the same.
1)  +
+ 
The two fractions are like fractions, so we add their numerators and keep the denominator the same. +
+  =
= 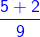 =
= 
2)  −
− 
Here, the given fractions are like fractions. So, we subtract their numerators and keep the denominator the same.
 −
−  =
= 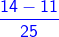 =
= 
2. Addition and Subtraction of two fractions with different denominators:
When we add or subtract unlike fractions we follow the following steps:
1)  +
+ 
The given fractions are unlike fractions, so we first find LCM of their denominators.
LCM of 8 and 24 = 2 × 2 × 2 × 3 = 24
Now, we convert the fractions into like fractions.
(Changing the denominator of fractions to 24)
 =
=  and
and
 +
+  = =
= = 
2)  -
- 
As the given fractions are unlike fractions, we find the LCM of their denominator.
LCM of 15 and 27 = 3 × 3 × 3 × 5 = 135
Next, we convert the fractions into like fractions
(Fractions with the same denominator)

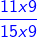 =
= 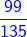 and
and 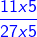 =
= 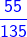
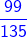 -
- 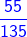 =
= 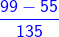 =
= 
Reciprocal of a Fraction
The reciprocal of a fraction is found by flipping the top and bottom numbers. For instance, the reciprocal of 2/3 is 3/2.
A Pinch of History
- In ancient India, fractions were known as bhinna in Sanskrit, which means "broken." They were also called bhaga or ansha, referring to "part" or "piece."
- The Bakshali manuscript is one of the oldest texts featuring fractions, dating back to around 300 CE, showcasing the historical use of fractions in India.
- This technique was utilised by renowned mathematicians like Aryabhata (c. 476–550 CE), Brahmagupta (598–668 CE), Sridharacharya (c. 750 CE), and Mahaviracharya (c. 817-875 CE).
- The notation of a line segment between the numerator and denominator in fractions was introduced by Al-Khwarizmi, a Persian mathematician, in the 9th century.
- Fractions also appeared in ancient cultures like Egypt and Babylon, primarily using fractional units where the numerator was 1. More complex fractions were expressed as sums of these units, known as Egyptian fractions.
- India was the first to introduce general fractions (where the numerator isn't necessarily along with rules for arithmetic operations like addition, subtraction, multiplication, and division.
- The Sulba-sutras from Vedic times indicate that Indians had established rules for working with fractions long ago.
- Brahmagupta formally outlined these rules and methods for fractions in a structured manner. His techniques for manipulating fractions are still applied today.
- For instance, Brahmagupta noted that to add or subtract fractions, you should equalise their denominators by multiplying the numerator and denominator of each fraction by the other denominators, then add or subtract the numerators.
- Indian ideas and methods regarding fractions were transmitted to Europe through the Arabs, greatly impacting the evolution of mathematics in Europe.
Let's Practice!
Question 1: Five balls together weight 1 kg. If they are roughly the same size, then what is the weight of each ball?
 View Answer
View Answer 
Answer: Total weight of five balls = 1 kg.
Therefore, the weight of each ball = 1/5 kg.
Question 2: Shade the parts of the figures according to the given fraction.
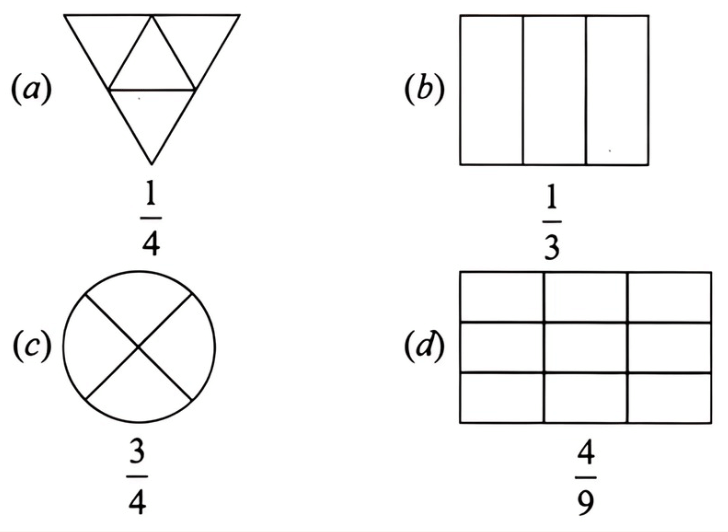
 View Answer
View Answer 
Answer: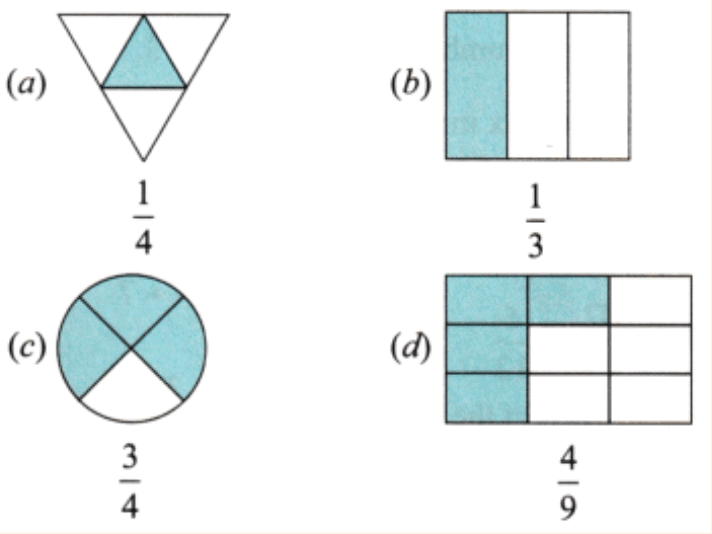
Question 2: Match each fractional unit with the correct picture.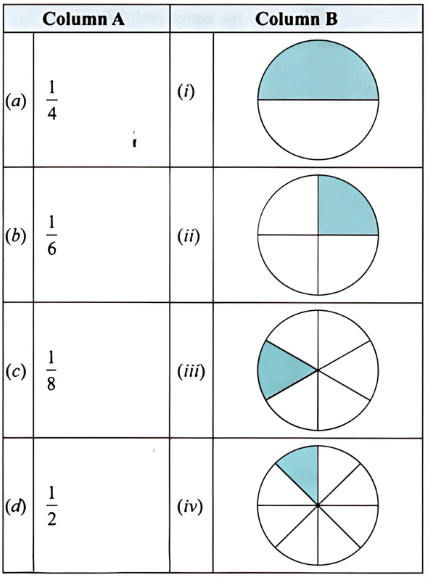
 View Answer
View Answer 
Answer: (a) – (ii), (b) – (iii),(c) – (iv), (d) – (i)
Question 3: Write the following fractions as mixed fractions.
(a) 8/3
(b) 12/7
(c) 25/9
 View Answer
View Answer 
Answer:
(a) 8/3 = 2 + 2/3 = 2 2/3
(b) 12/7 = 1 + 5/7 = 1 5/7
(c) 25/9 = 2 + 7/9 = 2 7/9
Question 4: Write these fractions appropriately as additions or subtractions.
 View Answer
View Answer 
Answer:
(a) 5/5 – 3/5 = 2/5
(b) 2/6 + 3/6 = 5/6
(c) 1/5 + 2/5 = 3/5
(d) 3/4 – 1/4 = 2/4
Key Points
- Fraction as Equal Share: A fraction is created when a whole is split into equal parts and shared fairly.
- Fractional Units: Each equal part of a whole is known as a fractional unit.
- Reading Fractions: In a fraction like 5/6, 5 is referred to as the numerator and 6 is the denominator.
- Proper and Improper Fractions: Proper fractions have a numerator smaller than the denominator (e.g., 1/2, 2/3). Improper fractions have a numerator that is equal to or larger than the denominator (e.g., 5/4, 6/6).
- Mixed Fractions: Mixed fractions consist of both a whole number and a fraction.
- Number Line: Fractions can be represented on a number line, with each fraction corresponding to a specific point.
- Equivalent Fractions: Fractions that show the same value or amount are known as equivalent fractions.
- Lowest Terms: A fraction is in its lowest terms when the numerator and denominator share no common factors apart from 1.
- Reciprocal of a Fraction: To find the reciprocal of a fraction, switch its numerator and denominator.
- Brahmagupta's Method for Adding Fractions: To add fractions, turn them into equivalent fractions with the same denominator and then add the numerators.
- Brahmagupta's Method for Subtracting Fractions: To subtract fractions, convert them to equivalent fractions with the same denominator and then subtract the numerators.
|
48 videos|334 docs|23 tests
|
FAQs on Fractions Chapter Notes - Mathematics for Class 6
| 1. What is the difference between a proper fraction and an improper fraction? |  |
| 2. How do you convert an improper fraction to a mixed number? |  |
| 3. What are equivalent fractions and how can I find them? |  |
| 4. How do you express a fraction in its simplest form? |  |
| 5. What is the role of fractions in measuring and sharing? |  |