The Other Side of Zero Chapter Notes | Mathematics for Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Bela’s Building of Fun |

|
| The Token Model |

|
| Integers in Other Places |

|
| Explorations with Integers |

|
| A Pinch of History |

|
| Practice Questions |

|
Introduction
In earlier classes, we learned about numbers like 1, 2, 3, and so on, which are used for counting. These are called positive numbers. But, what about numbers that are less than zero? In this chapter, we will explore these numbers, which are called negative numbers. Together, positive numbers, negative numbers, and zero form what we call integers.
We know that on a number line, numbers like 1, 2, 3, etc., are placed to the right of zero. But there are numbers that lie to the left of zero as well. These numbers are less than zero and are called negative numbers. For example, -1, -2, -3 are negative numbers.
Bela’s Building of Fun
Imagine a building with several floors above and below the ground. The ground floor is labeled as Floor 0. Floors above the ground are labeled with positive numbers (+1, +2, +3, etc.), while floors below the ground are labeled with negative numbers (-1, -2, -3, etc.).
Example:
- Floor 0: The ground floor.
- Floor +1: One floor above the ground.
- Floor -1: One floor below the ground.
 When you move up in the building, you use the ‘+’ button in the lift. For example, pressing ‘+2’ means moving up two floors. When you move down, you use the ‘-’ button. Pressing ‘-3’ means moving down three floors.
When you move up in the building, you use the ‘+’ button in the lift. For example, pressing ‘+2’ means moving up two floors. When you move down, you use the ‘-’ button. Pressing ‘-3’ means moving down three floors.
Numbering the Floors in the Building of Fun

- Entry to the Building of Fun starts at the ground floor, known as the Welcome Hall.
- From the ground floor:
- Press 1 to reach the Food Court on Floor 1.
- Press 2 to get to the Art Centre on Floor 2.
- To go to the Toy Store, press -1, which takes you to Floor -1.
- To visit the Video Games shop, press -2 for Floor -2.
- The ground floor is called Floor 0.
- This is because it serves as the starting point for the building's floor numbering.
- The Book Store is on Floor 3, which is the same number of floors you move when you press 3.
- Similarly, -3 is the floor number and also how many floors you go down when you press -3.
- A number with a + sign is called a positive number.
- A number with a - sign is called a negative number.
- In the Building of Fun, floors are numbered with the ground floor, Floor 0, as the reference point.
- Floors above the ground are numbered with positive numbers.
- To reach these, you press the + button multiple times.
- Floors below the ground are numbered with negative numbers.
- To access them, you press the - button several times.
- Zero is neither a positive nor a negative number.
- It does not have a + or - sign in front of it.
Addition to Keep Track of Movement
When you want to move between floors in a building using a lift, you can keep track of your movement by using a simple expression. Let's break it down:
- Starting Floor: This is where you begin your journey. In our example, we start from the Food Court, which is on floor +1.
- Movement: This is how many floors you go up or down. If you press the button for +2 in the lift, you are moving up 2 floors.
- Target Floor: This is where you end up after your movement. You can find it by adding the starting floor and the movement together.
Example: From the Food Court (+1), if you press +2 in the lift:
- Starting floor: +1 (Food Court)
- Movement: +2 (button pressed in the lift)
- Target floor:+1 + +2 = +3 (Book Store)
So, by pressing +2 in the lift from the Food Court, you reach the Book Store on floor +3.
Combining Button Presses is also Addition
When you press the '+' button, it's like adding floors, and pressing the '-' button is like subtracting floors. Let's see how Gurmit's button presses work out:
- Gurmit pressed the '+' button twice by mistake. This means he added two floors.
- Then, he quickly pressed the '-' button three times. This means he subtracted three floors.
- To find out where Gurmit ends up, we can combine these button presses into a simple expression:
- 2 (for the two '+' presses) - 3 (for the three '-' presses) = -1.
- This result means Gurmit will end up one floor below where he started in the Toy Store.
Back to Zero!

- Basant, in a hurry, accidentally presses +3 in the lift. To cancel this and stay on the ground floor, he can press -3. This action shows that (+3) + (-3) = 0, bringing him back to the starting point.
- The term -3 is known as the inverse of +3. Similarly, the inverse of +4 is -4.
- If Basant presses +4 and then -4 in the lift, he will return to the ground floor. This concept of inverse means that pressing a number and its opposite brings you back to zero, just like going from Floor +4 to Floor 0 by pressing -4, or from Floor -2 to Floor 0 by pressing +2.
Subtraction to Find Which Button to Press
Subtraction can be understood in different ways, such as 'taking away' or 'comparing quantities to make them equal.' For instance, if you have 10 books and I take away 4, I am left with 6. This can be expressed as 10 - 4 = 6. Similarly, if you have 10 rupees and my sister has 6 rupees, you can ask how much more she needs to have the same amount as me. This can be written as 6 + ? = 10 or 10 - 6 = ?.
When it comes to positive and negative numbers, we use the idea of making quantities equal or finding the missing number to be added.
For example, if you start at the Art Centre on the 2nd floor and want to go to the Sports Centre on the 5th floor, you need to press the button for +3 floors. This can be expressed using subtraction:
- Target floor - Starting floor = Movement needed.
- In this case, +5 (target floor) - +2 (starting floor) = +3 (movement needed).
Adding and Subtracting Larger Numbers
- A mine is a place where minerals are dug out of the ground. Minerals can be found both above and below the ground level.
- In the picture of the mine, there is a truck at the ground level, and a fast-moving lift that goes up and down a mineshaft. This lift carries people and ore (the minerals).
- Ground level is marked as 0.
- Levels above the ground are marked with positive numbers, and levels below the ground are marked with negative numbers.
- The number next to each level tells you how many meters above or below ground level it is.
In the mine, just like in the Building of Fun: Starting level + Movement = Target level.
For example: (-90) + (-55) = -145
= + 100
Target level — Starting level = Movement needed.
For example: (+ 40) — (50) = + 90
How Many Negative Numbers Are There?
Imagine a tall building with six floors above the ground and five floors below. The floors above represent positive numbers like +1, +2, +3, and so on, going up without limit. The floors below represent negative numbers like -1, -2, -3, continuing downward. The ground floor is 0, which acts as the starting point. When we combine positive numbers, negative numbers, and zero, we get integers.
In the building example:
- The floors above ground range from +1 to +6.
- The floors below ground range from -5 to 0.In a larger example, like a mine, we can have numbers from -200 to +180. But just like with the building, negative numbers keep going down without an end, just like positive numbers keep going up.
So, the pattern of numbers looks like this:
- Negative numbers: -4, -3, -2, -1
- Zero: 0
- Positive numbers: 1, 2, 3, 4, ...
These numbers, both positive and negative, along with zero, are called integers. They go in both directions from zero, creating an endless line of numbers in each direction.
Adding, Subtracting, and Comparing any Numbers
To add and subtract even larger integers, we can imagine even larger lifts! In fact, we can imagine a lift that can extend forever upwards and forever downwards, starting from Level 0. There does not even have to be any building or mine around - just an 'infinite lift'!
We can use this imagination to add and subtract any integers we like. For example, suppose we want to carry out the subtraction + 2000 - (-200). We can imagine a lift with 2000 levels above the ground and 200 below the ground.
- Recall that Target level - Starting level = Movement needed.
- To go from the Starting Floor -200 to the Target Floor + 2000, we must press +2200(+ 200 to get to zero, and then +2000 more after that to get to + 2200).
- Therefore, (+ 2000) - (—200) = + 2200.
- Notice that (+ 2000) + (+ 200) is also +2200.
Back to the Number Line
- The "infinite lift" we saw earlier closely resembles a number line.
- By rotating it 90 degrees, it essentially transforms into a number line.
- This also explains how to extend a number ray into a full number line, addressing a question we had at the start of the chapter.
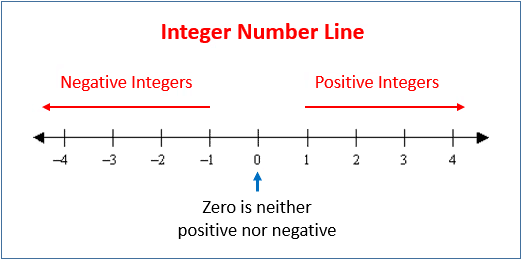
- On the left side of 0, we find the negative numbers: -1, -2, -3, and so on.
- For positive numbers, we usually omit the + sign and simply write them as 1, 2, 3, ...
Visual Representation of the Number Line:
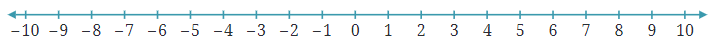
- Instead of using a lift to move along the number line, we can imagine walking on it.
- To the right is the positive (forward) direction, and to the left is the negative (backward) direction.
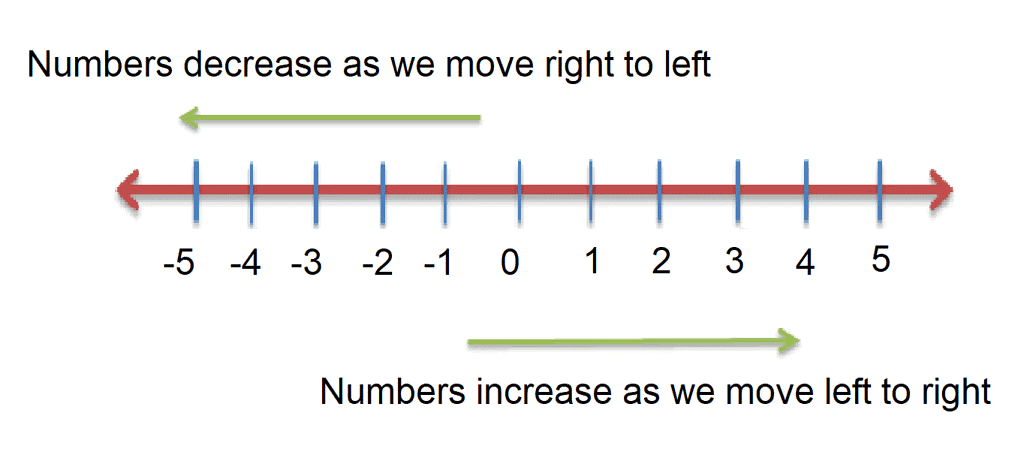
- On the number line, smaller numbers are to the left of bigger numbers, and bigger numbers are to the right of smaller numbers. For example:
- 2 < 5 (2 is less than 5)
- -3 < 2 (negative 3 is less than 2)
- -5 < -3 (negative 5 is less than negative 3)
Using the Unmarked Number Line to Add and Subtract
- Just like you can use a number line to add, subtract, and compare small numbers, you can also do the same with large numbers by imagining an "infinite number line" or drawing an "unmarked number line."
- This unmarked number line shows only the position of zero, without marking other numbers. It can be helpful for adding and subtracting integers. You can either show or imagine the scale of the number line and the positions of numbers on it.
- For example, in the unmarked number line (UNL) below, we can see the addition problem: 85 + (-60) = ?:
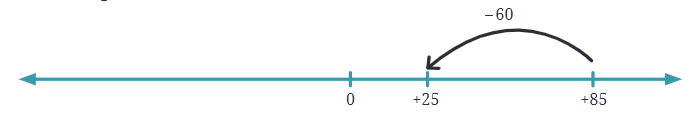
- From this UNL, we can visualize that 85 + (-60) = 25.
- The following UNL illustrates a subtraction problem that can also be seen as a missing addend problem: (-100) - (+250) = ? or 250 + ? = -100.

- From this, we can visualize that ? = -350 in this problem.
- In this way, you can perform addition and subtraction problems with positive and negative numbers, either on paper or in your head, using an unmarked number line.
Converting subtraction to addition and addition to subtraction
- Convert subtraction to addition and addition to subtraction.
- Remember that Target floor - Starting floor = Movement needed.
- Alternatively, Target floor = Starting floor + Movement needed.
- If we start at 2 and want to reach -3, what is the movement needed?
- First method: Looking at the number line, we see we need to move -5 (which is 5 spaces in the backward direction).
- Therefore, from 3 to 2, the movement needed is -5.
- Second method: Break the journey from 2 to -3 into two parts:
- From 2 to 0, the movement is 0 - 2 = -2.
- From 0 to -3, the movement is -3.
- The total movement is the sum of the two movements: -3 + -2 = -5.
- Notice that in the second method, there is no subtraction involved!
- This way, we can always change subtraction into addition. The number being subtracted can be replaced by its inverse and then added.
- In the same way, a number that is being added can be replaced by its inverse and then subtracted. This allows us to convert addition into subtraction.
- Example: -3 -(-2) = -3 + 2 = -1.
The Token Model
Using Tokens for Addition
- In Bela's Building of Fun, the lift attendant uses tokens to keep track of his activities. Positive tokens are red and negative tokens are black.
- When he presses the '+' button, he takes a positive token, and when he presses the '-' button, he takes a negative token.
- After one hour, he checks his pocket and finds 5 positive tokens and 3 negative tokens.
- To find out which floor he is on, we can calculate the total by adding the positive and negative tokens: (+5) + (-3) = +2

- This means he is at Floor +2.
- Another way to understand this is by using the concept of "zero pairs." A positive token and a negative token cancel each other out because their combined value is zero.
- For example, when he has one positive token and one negative token, it represents pressing '+' once and '-' once, which cancel each other. This is called making a "zero pair."
- When we remove all the zero pairs from his tokens, we are left with the excess tokens. In this case, he has two positive tokens left after removing the zero pairs.
- So, (+5) + (-3) = +2
- This method of using tokens can be applied to any addition problem!
Using Tokens for Subtraction
- Subtraction with Tokens: We can subtract numbers using tokens, just like we do with addition.
- Example of Subtraction: To subtract, if you have 5 positive tokens and you take away 4 positive tokens, you will see the result.
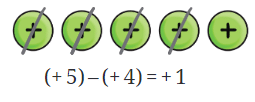
- Comparing Expressions: Is (-7) - (-5) the same as (-7) + 5? This is a question about how subtraction and addition relate to each other.
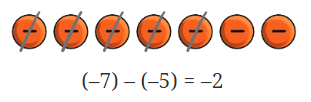
- Another Example: Let’s consider (5) - (6).

- Start with 5 positive tokens.
- When you try to take away 6 positive tokens, you find out that there aren't enough tokens to remove!
Integers in Other Places
Integers are useful in many real-world scenarios:
- Banking: Credits are positive numbers, and debits are negative numbers. Your bank balance can be positive or negative.
Example: Ravi had ₹500 in his bank account.
He withdrew ₹200 to buy a new bag.
Then, he deposited ₹150 into his account.What is the balance in Ravi’s account now?
Solution:
Starting amount = ₹500
Withdrawal (money taken out) = -₹200
Deposit (money added) = +₹150
Final balance = 500 - 200 + 150 = ₹450
Ravi’s account balance is ₹450.
- Geography: Heights above sea level are positive, and depths below sea level are negative.
Example: A submarine is floating 60 metres below sea level.
It then dives 30 metres deeper, and later rises 50 metres toward the surface.What is the submarine’s final position relative to sea level?
Solution:
Initial position = –60 metres
Dives deeper = –30 metres → –60 – 30 = –90 metres
Rises = +50 metres → –90 + 50 = –40 metres
The submarine is 40 metres below sea level.
- Temperature: Temperatures above freezing are positive, and those below freezing are negative.
Example: The temperature in Shimla was 5°C in the morning.
By evening, the temperature dropped by 12°C.What was the temperature in Shimla in the evening?
Solution:
Morning temperature = 5°C
Drop in temperature = –12°C
Evening temperature = 5 – 12 = –7°C
The temperature in the evening was –7°C.
 |
Download the notes
Chapter Notes: The Other Side of Zero
|
Download as PDF |
Explorations with Integers
A Hollow Integer Grid
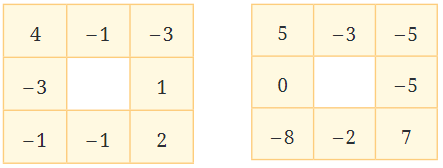 Let's Investigate:
Let's Investigate:
- Top Row: Bottom Row: (-1) (-1) 2
- Left Column: Right Column: (-3) 1 2
In every grid, the numbers in both the top and bottom rows, as well as the numbers in the leftmost and rightmost columns, all add up to the same total. We will refer to this total as the border sum. The border sum for the first grid is 0.
An Amazing Grid of Numbers!
- Below is a grid with some numbers. Follow the steps shown below until no number is left.
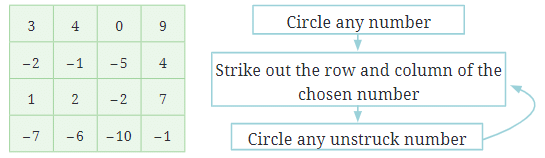
- Circle any number.
- Strike out the row and column of the chosen number.
- Circle an unstruck number.
- When there are no more unstruck numbers, STOP. Add the circled numbers.
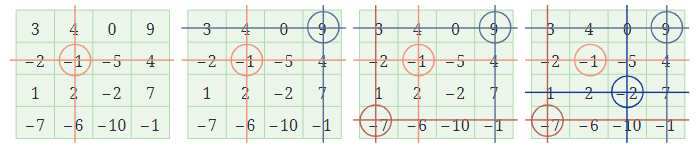
In the example below, the circled numbers are -1, 9, -7, and -2. When you add them together, you get -1.
A Pinch of History
Negative Numbers in Ancient India
- Negative numbers were first used in Asia, particularly in ancient China and India, for accounting purposes.
- In China, the Nine Chapters on Mathematical Art(Jiuzhang Suanshu), a mathematical work from the first or second century CE, used red and black rods to represent positive and negative numbers.
- In India, ancient texts like the ArthaShästra by Kautilya and the Bakshali Manuscript from around 300 CE also recognized negative numbers in accounting. The Bakshali Manuscript used a special symbol to indicate negative numbers.
Brahmagupta's Contributions
- Brahmagupta, in his work Brähma-sphuta-siddhänta around 628 CE, treated positive numbers, negative numbers, and zero as equally valid and provided rules for arithmetic operations on all these numbers.
- His rules for addition and subtraction laid the foundation for modern arithmetic, allowing operations with positive, negative, and zero numbers.
Brahmagupta's Rules for Addition (Brähma-sphuta-siddhänta 18.30, 628 CE)
- The sum of two positives is positive (e.g., 2 + 3 = 5).
- The sum of two negatives is negative. To add two negatives, add the numbers (without the signs), and then place a minus sign to obtain the result (e.g., (—2) + (—3) = —5).
- To add a positive number and a negative number, subtract the smaller number (without the sign) from the greater number (without the sign), and place the sign of the greater number to obtain the result (e.g., -5 + 3 = -2 and -3 + 5 = 2).
- The sum of a number and its inverse is zero (e.g., 2 + (-2) = 0).
- The sum of any number and zero is the same number (e.g., -2 + 0 = -2 and 0 + 0 = 0).
Brahmagupta's Rules for Subtraction (Brahma-sphuta-siddhänta 18.31-18.32)
- If a smaller positive is subtracted from a larger positive, the result is positive (e.g., 3 - 2 = 1).
- If a larger positive is subtracted from a smaller positive, the result is negative (e.g., 2 - 3 = -1).
- Subtracting a negative number is the same as adding the corresponding positive number (e.g., 2 - (-3) = 2 + 3).
- Subtracting a number from itself gives zero (e.g., 2 - 2 = 0 and -2 - (-2) = 0).
- Subtracting zero from a number gives the same number (e.g., -2 - 0 = -2 and 0 - 0 = 0). Subtracting a number from zero gives the number's inverse (e.g., 0 - (-2) = 2).
Brahmagupta's Legacy
- Brahmagupta was the first to treat zero, positive numbers, and negative numbers equally and provided rules for arithmetic operations on all these numbers, forming what is now known as a ring.
- His ideas revolutionized mathematics, but it took centuries for the rest of the world to accept zero and negative numbers as legitimate.
- These concepts were transmitted to the Arab world by the 9th century and to Europe by the 13th century.
- Despite initial resistance in Europe, where negative numbers were considered 'absurd' by some mathematicians, over time zero and negative numbers became essential in mathematics and science.
- Today, they are regarded as critical numbers, just as Brahmagupta envisioned over 1,400 years ago.
- The abstraction of arithmetic rules for all numbers laid the groundwork for the development of algebra.
Practice Questions
1. Which number is greater?
a) -7 or -2
b) -4 or 0
 View Answer
View AnswerAnswer:
When comparing negative numbers, the number closer to zero is always greater. Think of a number line where numbers on the right are bigger than those on the left.
- -2 is greater than -7 because -2 is closer to 0 than -7.
- 0 is greater than -4 because zero is neither positive nor negative and is always bigger than any negative number.
2. Find the missing number in the sequence:
_, -6, -4, _, 0, _, 4
 View Answer
View AnswerAnswer:
The pattern increases by +2 each time.
Filled sequence: -8, -6, -4, -2, 0, 2, 4
Missing numbers: -8, -2, 2
3. Solve the following:
a) (-5) + (+8) = ?
b) (+10) - (-3) = ?
 View Answer
View AnswerAnswer:
- (-5) + (+8) = 3 → If you owe ₹5 and receive ₹8, you will have ₹3 left.
- (+10) - (-3) = 13 → Subtracting a negative is the same as adding, so 10 + 3 = 13.
4. A diver is 20 meters below sea level. He swims up 15 meters. What is his new position?
 View Answer
View AnswerAnswer:
Starting position: -20 meters (below sea level). Moving up means adding: (-20) + (+15) = -5 meters.
New position: -5 meters (below sea level)
5. A shopkeeper had a debt of ₹250. He paid back ₹100. How much does he still owe?
 View Answer
View AnswerAnswer:
Debt starts at -250. Paying back ₹100 means adding: (-250) + (+100) = -150.
Remaining debt: ₹150
|
52 videos|287 docs|23 tests
|
FAQs on The Other Side of Zero Chapter Notes - Mathematics for Class 6
| 1. What is the Token Model in relation to integers? |  |
| 2. How do integers appear in real-life situations? |  |
| 3. Why is it important to learn about integers in Class 6? |  |
| 4. What historical significance do integers hold in mathematics? |  |
| 5. What are some effective strategies for practicing integers? |  |

























