All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Notes  >  Quantitative Aptitude/संख्यात्मक योग्यता  >  महत्वपूर्ण सूत्र: संख्या प्रणाली

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams PDF Download

CAT जैसी प्रतियोगी परीक्षाओं के लिए संख्या प्रणाली को समझना महत्वपूर्ण है, क्योंकि यह विभिन्न मात्रात्मक विषयों के लिए आधार बनाता है । यह विषय दिलचस्प वैचारिक समस्याओं के लिए जाना जाता है जो सर्वश्रेष्ठ दिमाग का परीक्षण करते हैं। केवल समस्याओं को हल करने के बजाय, अवधारणाओं को अच्छी तरह से समझने पर ध्यान केंद्रित करें। प्रश्नों को हल करने के लिए वैकल्पिक तरीकों का पता लगाएं, क्योंकि यह आपकी समस्या-समाधान कौशल को बढ़ाता है और आपको परीक्षा के लिए व्यापक रूप से तैयार करता है।

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

संख्या प्रणाली क्या है?

संख्या प्रणाली संख्या रेखा पर किसी संख्या को दर्शाने की एक विधि है। संख्या प्रणाली संख्याओं को लिखने या व्यक्त करने की एक प्रणाली है। इस पृष्ठ पर आगे संख्या प्रणाली के सूत्र और परिभाषाएँ दी गई हैं।

 यहां उन महत्वपूर्ण सूत्रों की सूची दी गई है  , जिन्हें उम्मीदवारों को परीक्षा में सफलतापूर्वक उत्तीर्ण होने के लिए आवश्यक है।

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

Clear all your Bank Exams doubts with EduRev

बीजगणित में महत्वपूर्ण सूत्र

बीजगणित गणित की एक शाखा है जिसमें संख्याओं के स्थान पर अक्षरों का प्रयोग किया जाता है। बीजगणितीय समीकरण एक पैमाने को दर्शाता है, जो एक संख्या के साथ पैमाने के एक तरफ किया जाता है, वह पैमाने के दोनों तरफ भी किया जाता है।  

  • (ए + बी)(ए - बी) = (ए 2 - बी 2 )
  • (ए + बी) 2 = (ए 2 + बी 2 + 2एबी)
  • (ए - बी) 2 = (ए 2 + बी 2 - 2एबी)
  • (ए + बी + सी) 2 = ए 2 + बी 2 + सी 2 + 2(एबी + बीसी + सीए)
  • (ए 3 + बी 3 ) = (ए + बी)(ए 2 - एबी + बी 2 )
  • (ए 3 - बी 3 ) = (ए - बी)(ए 2 + एबी + बी 2 )
  • (a 3 + b 3 + c 3 - 3abc) = (a + b + c)(a 2 + b 2 + c 2 - ab - bc - ac)
    ⇒ जब a + b + c = 0, तो a 3 + b 3 + c 3 = 3abc
  • (a + b) n  = a n + ( n C 1 )a n -1 b + ( n C 2 )a n -2 b² + … + ( n C n-1 )ab n-1 + b n

बीजगणित में सूत्रों का दृश्य प्रतिनिधित्व

  • (a + b) 2= a 2 + b 2 + 2ab
    (a + b) 2  सूत्र बीजगणितीय पहचान है जिसका उपयोग दो संख्याओं के योग का वर्ग ज्ञात करने के लिए किया जाता है। (a + b) 2 के रूप में द्विपद का सूत्र ज्ञात करने के लिए , हम बस (a + b) (a + b) को गुणा करेंगे।
    (a + b) 2 = (a + b)(a + b)
    = a 2  + ab + ba + b 2
    = a 2 + 2ab + b 2
    इसलिए, (a + b) 2 सूत्र है: (a + b) 2 = a 2 + 2ab + b 2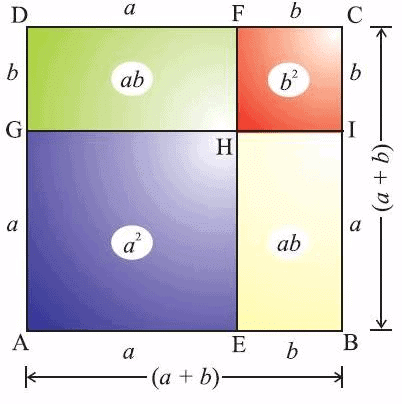महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
  • (a + b + c) 2= a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
    (a + b + c) 2 सूत्र का उपयोग तीन संख्याओं के वर्गों का योग ज्ञात करने के लिए किया जाता है, बिना वास्तव में वर्गों की गणना किए। (a + b + c) 2 सूत्र प्रमुख बीजीय पहचानों में से एक है। (a + b + c) 2 सूत्र का विस्तार प्राप्त करने के लिए हम (a + b + c) को स्वयं से गुणा करते हैं, जिससे (a + b + c) 2 प्राप्त होता है ।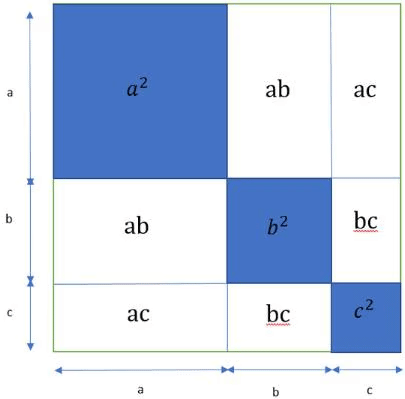
    महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
This doc is part of
223 docs|265 tests
Join course for free
Join course for free

संख्या प्रणाली में महत्वपूर्ण सूत्र

  1. 1 + 2 + 3 + 4 + 5 + … + n = n(n + 1)/2
    उदाहरण:  पहली 35 प्राकृतिक संख्याओं का योग ज्ञात करें। 
    ​हल: दिया गया है, n = 35 
    ​प्राकृतिक संख्याओं के योग का सूत्र है: 
    ​S = [n(n+1)]/2 
    ​S = [35(35+1)]/2 
    ​S = 630
  2. (1² + 2² + 3² + ….. + n²) = n ( n + 1 ) (2n + 1) / 6
    उदाहरण: पहले 40 प्राकृतिक संख्याओं के वर्गों का योग ज्ञात करें।
    समाधान:  प्राकृतिक संख्याओं के वर्गों के योग का सूत्र इस प्रकार दिया गया है:
    Σn 2 = [n(n+1)(2n+1)]/6
    यहाँ, n = 40
    Σ40² = (40/6) (40 + 1)(2 x 40 + 1)
    Σ40² = (20/3) (41)(81)
    Σ40² = (20)(41)(27)
    Σ40² = 22140
  3. (1³ + 2³ + 3³ + ….. + n³) = (n(n + 1)/ 2)²
    उदाहरण:  5 से 14 तक की प्राकृतिक संख्याओं के घनों का योग ज्ञात करें।
    समाधान: 5 से 14 तक की संख्याओं के घनों का योग ज्ञात करने के लिए, हम सबसे पहले पहली 14 प्राकृतिक संख्याओं के घनों का योग ज्ञात करेंगे और फिर हम पहली 4 प्राकृतिक संख्याओं के घनों का योग ज्ञात करेंगे। फिर हम उत्तर प्राप्त करने के लिए प्राप्त मानों को घटाते हैं।
    n प्राकृतिक संख्याओं के घनों का योग = [n (n + 1)] 2 /4
    प्रथम 14 प्राकृतिक संख्याओं के घनों का योग = (14 × (14+1)) 2 /4
    = (14 × 15) 2 /4
    = (210) 2 /4
    = 44100/4 = 11025
    अब, प्रथम 4 प्राकृतिक संख्याओं के घनों का योग = (4 × (4+1)) 2 /4
    = (4 × 5) 2 /4
    = (20) 2 /4
    = 100
    इसलिए, 5 से 14 तक प्राकृतिक संख्याओं के घनों का योग = 11025 - 100 = 10925.
  4. प्रथम n विषम संख्याओं का योग = n²
    उदाहरण:1 से 50 तक विषम संख्याओं का योग ज्ञात कीजिए।

    हल: हम जानते हैं कि 1 से 50 के बीच 25 विषम संख्याएँ हैं। इस प्रकार, n विषम संख्याओं के योग का सूत्र जो n 2 है , का उपयोग करके, हमें S 25  = 25 2 = 625 मिलता है। 
    हम इसे वैकल्पिक रूप से S n= n/2 × [a + l] सूत्र का उपयोग करके दिखा सकते हैं । हम जानते हैं कि 1 से 50 तक विषम संख्याओं का योग S n = 1 + 3 + ... + 49 के रूप में दर्शाया जाता है।
    इस प्रकार, a = 1, l = 49, और n = 25.
    S 25 = (25/2) × [1 + 49]

    = (25/2) × 50

    = 25 × 25 = 625
    इस प्रकार, 1 से 50 तक की विषम संख्याओं का योग 625 के बराबर है।

  5. प्रथम n सम संख्याओं का योग = n (n + 1)

    उदाहरण: 1 से 50 तक सम संख्याओं का योग क्या है? 
    हल: हम जानते हैं कि 1 से 50 तक 25 सम संख्याएँ हैं।
    इस प्रकार, n = 25
    सम संख्याओं के योग के सूत्र से हम जानते हैं;
    Sn = n(n+1)
    Sn = 25(25+1) = 25 x 26 = 650

  6. m! में n की उच्चतम घात [m/n] + [m/n 2 ] + [m/n 3 ] +….. है, जहाँ, [x] x से छोटा या बराबर सबसे बड़ा पूर्णांक है।
    उदाहरण:  100! में 7 की उच्चतम घात ज्ञात करें।
    100! में 7 की उच्चतम घात = [100/7] + [100/49] = 16

  7. n! में शून्यों की संख्या ज्ञात करने के लिए n! में 5 की उच्चतम घात ज्ञात कीजिए।
    उदाहरण: 23! में अंतिम शून्यों की संख्या क्या है?

    [23/5] = 4. यह 5 से कम है, इसलिए हम यहीं रुकते हैं। उत्तर 4 है।

  8. यदि n अलग-अलग अंकों के सभी संभावित क्रमचयों को एक साथ जोड़ा जाए तो योग
    =  (n-1)! * (n अंकों का योग) * (11111… n बार)
    उदाहरण: उन सभी संख्याओं का योग क्या होगा जो एक साथ अंक 1, 3, 5, 7 का उपयोग करके बनाई जा सकती हैं और जिनमें कोई अंक दोहराया नहीं गया है?
    समाधान: सभी दिए गए n अंकों को लेकर बनाई गई संख्याओं का योग (सभी n अंकों का योग) * (n - 1)! * (111…..n बार) है।
    यहां n = 4, और 4 अंकों का योग = 16
    अंक 1, 3, 5, 7 का उपयोग करके बनाई जा सकने वाली सभी संख्याओं का योग = (16) * (4 - 1)! * ( 1111) = 16 * 3! * 1111

  9. यदि संख्या को N = a p ∗ b q  ∗ c r के रूप में दर्शाया जा सकता है । तब, N के कारकों की संख्या (p+1) * (q+1) * (r+1) है
    । सभी कारकों का योग: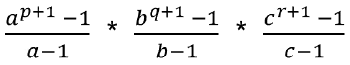 
    महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
    उदाहरण:  98 के कारकों की संख्या ज्ञात कीजिए और सभी कारकों का योग और गुणनफल भी ज्ञात कीजिए। 
    समाधान:  सबसे पहले, संख्या 98 को अभाज्य गुणनखंडों में लिखें। 
    अर्थात  98 = 2 × 49 = 2 × 7 × 7  = 2 1 x 7 2    
    यहाँ A = 2, B = 7, p = 1, q = 2 
    98 के कारकों की संख्या  = (p + 1)(q +1) = 2 × 3 = 6 
    98 के सभी कारकों का योग =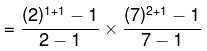महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams  3 × 57 = 171 
    ​संख्या 98 के सभी कारकों का गुणनफल  = (98) 6/2 = 941192

  10. यदि कारकों की संख्या विषम है, तो N एक  पूर्ण वर्ग है ।
    उदाहरण:  4500 के विषम, सम, पूर्ण वर्ग, पूर्ण घन कारकों की संख्या ज्ञात कीजिए ।
    4500 = 45 × 100 = 9 × 5 × 10 × 10  = 3 × 3 × 5 × 5 × 2 × 5 × 2  = 2 2 × 3 2 × 5 3  
    यहाँ,  A = 2, B = 3, C = 5, p = 2, q = 2 और r = 3 पर विचार करें।
    यहाँ पहचान करने पर कि विषम संख्या 3 और 5 हैं।
    संख्या 4500 के विषम कारकों की संख्या  = (q + 1) (r + 1) = 3 × 4 = 12
    ∴ कारकों की कुल संख्या  = (p + 1)(q +1)(r +1) = 3 × 3 × 4 =36
    संख्या के सम कारकों की संख्या  = (कुल कारकों की संख्या – विषम कारकों की संख्या)  = 36 – 12 = 24
    संख्या 4500 के पूर्ण वर्ग गुणनखंडों की संख्या  = 2 x 2 x 2 = 8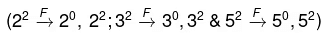 
    महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
    ​संख्या 4500 के पूर्ण घन गुणनखंडों की संख्या  = 1 x 1 x 2 = 2

  11. मान लीजिए एक संख्या N है और यदि संख्या N और 1 को मिलाकर n कारक हैं, तो कारकों के जोड़े की संख्या n/2 होगी। यदि N एक पूर्ण वर्ग है, तो जोड़े की संख्या (वर्गमूल सहित)  (n+1)/2 है।
    उदाहरण:  36 को आप कितने तरीकों से इसके दो कारकों के गुणनफल के रूप में व्यक्त कर सकते हैं?
    36 का अभाज्य गुणनखंडन यानी हम लिखते हैं 36 = 2 2 × 3 2
    36 के कारकों की संख्या (2+1)(2+1) = 9 होगी
    (यानी कारक 1, 2,3, 4, 6, 9, 12, 18, 36 हैं)। 
    चूंकि हमसे कुल तरीकों की संख्या पूछी गई है इसलिए हम 36 का वर्गमूल यानी 6 भी शामिल करते हैं।

  12. यदि संख्या को  N = 2 p ∗ a q ∗ b r के रूप में व्यक्त किया जा सकता है । जहाँ 2 की घात p है और a, b अभाज्य संख्याएँ हैं तो:
    (i)  N के सम गुणनखंडों की संख्या =  p (1 + q) (1 + r) । . .
    (ii)  N के विषम गुणनखंडों की संख्या = (1 + q) (1 + r)…

  13. जब हमें यह गणना करने के लिए कहा जाता है कि समीकरण X 2 - Y 2 = N के लिए कितने सकारात्मक अभिन्न समाधान संभव हैं  , तो 4 मामले हो सकते हैं।
    आइए उदाहरणों को हल करके एक-एक करके उन्हें देखें:
    समीकरण X 2 - Y 2 = N के लिए सकारात्मक अभिन्न समाधान? जब हमें यह गणना करने के लिए कहा जाता है कि समीकरण X 2 - Y 2
    = N के लिए कितने सकारात्मक अभिन्न समाधान संभव हैं , तो 4 मामले हो सकते हैं। 
    केस 1: N एक विषम संख्या है और एक पूर्ण वर्ग नहीं है 
    केस 2: N एक विषम संख्या और एक पूर्ण वर्ग है 
    केस 3:  N एक सम संख्या है और एक पूर्ण वर्ग नहीं है 
    केस 4:  N एक सम संख्या और एक पूर्ण वर्ग है 
    केस 1: N एक विषम संख्या है और एक पूर्ण वर्ग नहीं है सकारात्मक अभिन्न समाधानों की कुल संख्या = (N के कारकों की कुल संख्या) / 2 
    उदाहरण:  समीकरण X 2  - Y 2  = 135 के लिए कितने सकारात्मक अभिन्न समाधान संभव हैं ? 135 = 1, 3, 5, 9, 15, 27, 45 और 135 के कारकों की कुल संख्या  8 है । 
    इसलिए, सकारात्मक अभिन्न समाधानों की कुल संख्या = 8/2 = 4. 
    स्थिति 2: N एक विषम संख्या है और एक पूर्ण वर्ग है सकारात्मक अभिन्न समाधानों की कुल संख्या = [(N के कारकों की कुल संख्या) - 1] / 2 होगी 
    उदाहरण: समीकरण X 2 - Y 2  = 121 के लिए कितने सकारात्मक अभिन्न समाधान संभव हैं ? 
    121 =  1, 11 और 121  के कारकों की कुल संख्या 3 है। 
    इसलिए, सकारात्मक अभिन्न समाधानों की कुल संख्या = (3-1) / 2 = 1 
    स्थिति 3: N एक सम संख्या है और एक पूर्ण वर्ग नहीं है सकारात्मक अभिन्न समाधानों की कुल संख्या = [(N / 4) के कारकों की कुल संख्या] / 2 होगी 
    उदाहरण: समीकरण X 2 - Y 2  = 160 के लिए कितने सकारात्मक अभिन्न समाधान संभव हैं? 40 के कारकों की कुल संख्या =  1, 2, 4, 5, 8, 10, 20 और 40 8 है (क्योंकि N = 160 और N/4 = 40) 
    इसलिए, कुल सकारात्मक समाकल समाधानों की संख्या = 8/2 = 4 
    स्थिति 4 : N एक सम संख्या है और एक पूर्ण वर्ग है सकारात्मक समाकल समाधानों की कुल संख्या होगी = {[(N/4) के कारकों की कुल संख्या] – 1 } / 2 
    उदाहरण: समीकरण X 2 – Y 2 = 256 के लिए कितने सकारात्मक समाकल समाधान संभव हैं? 64 के कारकों की कुल संख्या =  1, 2, 4, 8, 16, 32 और 64 और 7 है (क्योंकि N = 256 और N/4 = 64)
    इसलिए, (7-1)/2 = 3 सकारात्मक समाकलन समाधान।
    एडुरेव टिप:  किसी संख्या को दो वर्गों के योग के रूप में लिखा जा सकता है  , जिसमें 4k + 3 के रूप के अभाज्य गुणनखंड शामिल हों, जब तक  कि उन अभाज्य गुणनखंडों को सम घात तक बढ़ाया जाता है।

  14.  a b में अंकों की संख्या = [b log m (a)] + 1 ; जहाँ m संख्या का आधार है और [.] सबसे बड़ा पूर्णांक फ़ंक्शन दर्शाता है।

  15. यहां तक ​​कि वह संख्या जो 4 का गुणज नहीं है, उसे कभी भी 2 पूर्ण वर्गों के अंतर के रूप में व्यक्त नहीं किया जा सकता।

  16. मूल योग गुण:
    (i)  पहली n विषम संख्याओं का योग  n 2
    है (ii) पहली n सम संख्याओं का योग n(n + 1) है
    (iii)  1 + 2 + 3 + 4 + 5 + … + n = n(n + 1)/2
    (iv)  (1 ² + 2 ² + 3 ² + ….. + n ² ) = n ( n + 1 ) (2n + 1) / 6
    (v)  (1 ³ + 2 ³ + 3 ³ + ….. + n ³ ) = (n(n + 1)/ 2)²

  17. N के गुणनखंडों का गुणनफल N a/2 द्वारा दिया जाता है , जहाँ  'a' गुणनखंडों की संख्या है।

  18. a के अंतिम दो अंक 2 , (50 – a) 2 , (50 + a) 2 , (100 – a) 2 . . . . समान हैं। प्रत्येक संख्या को (50n ± x) के रूप में लिखा जा सकता है, जहाँ x 0 से 25 तक की संख्या है। इस प्रकार 50n, इसका अर्थ केवल 50 का कोई गुणज यानी 0, 50, 100, 150, ……
    0 से 25 = (0 से 25) स्वयं है।
    25 से 50 = 50 – (25 से 0)
    50 से 75 = 50 + (0 से 25)
    75 से 100 = 100 – (25 से 0)
    100 से 125 = 100 + (0 से 25)
    125 से 150 = 150 – (25 से 0) इत्यादि।

    लेकिन यह हमें किसी वर्ग के अंतिम दो अंक ज्ञात करने में किस प्रकार मदद करता है?
    (50n ± x) 2 = 2500n 2 ± 100nx + x 2 2500n 2
    और 100nx में से प्रत्येक के अंतिम दो अंक 00 होंगे। इस प्रकार RHS के अंतिम दो अंक, और इसलिए LHS के भी, x 2 के अंतिम दो अंक होंगे ।

    उदाहरण: 268 2 के अंतिम दो अंक क्या हैं ? 

    268 = 50 × 5 + 18. इस प्रकार, 268 2
    के अंतिम दो अंक 18 2 के अंतिम दो अंक अर्थात 24 के समान होंगे ।

    उदाहरण: 278 2 के अंतिम दो अंक क्या हैं ? 

    जबकि आप 278 = 50 × 5 + 28 पर विचार कर सकते हैं, यह
    278 = 50 × 6 - 22, को 0 से 25 की सीमा में x मानेगा। इस प्रकार, 278 2
    के अंतिम दो अंक 22 2 के अंतिम दो अंकों के समान होंगे अर्थात 84।

  19. यदि संख्या को 2 10 n के रूप में लिखा जाता है :
    (i)  जब n विषम है, तो अंतिम 2 अंक 24 हैं।
    (ii)  जब n सम है, तो अंतिम 2 अंक 76 हैं।
Download the notes
महत्वपूर्ण सूत्र: संख्या प्रणाली
 Download as PDF
Download as PDF

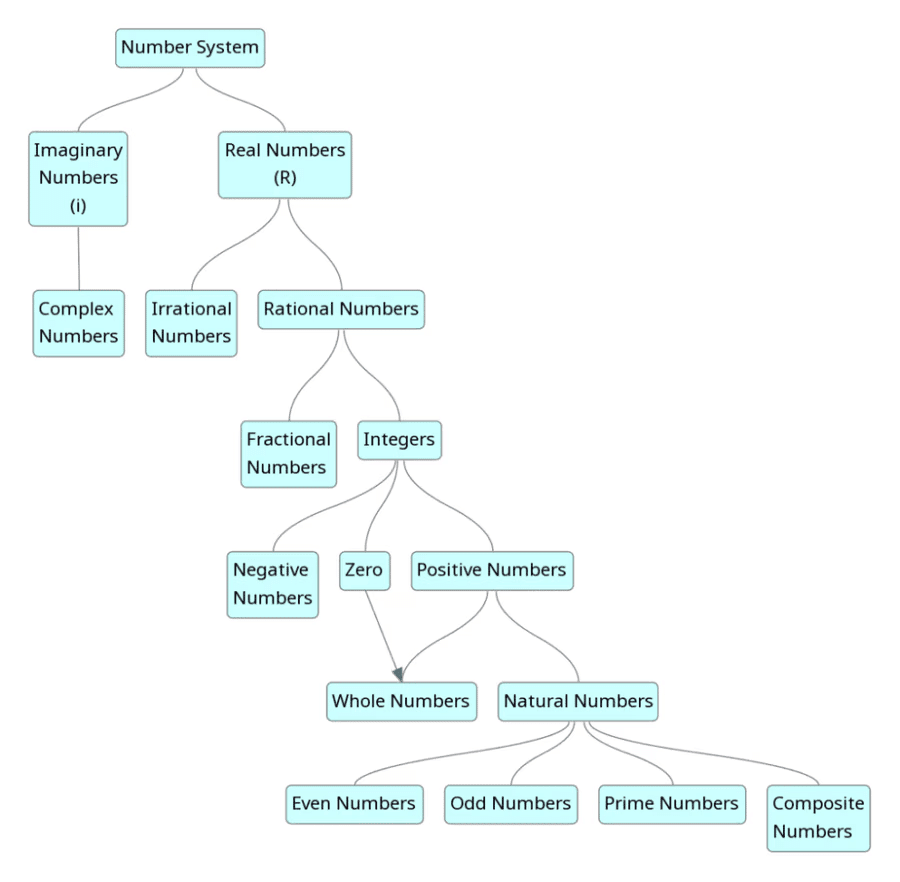
संख्याओं के प्रकार

  1. प्राकृतिक संख्याएँ
    सभी धनात्मक पूर्णांकों को प्राकृतिक संख्याएँ कहते हैं। 1 से अनंत तक की सभी गिनती संख्याएँ प्राकृतिक संख्याएँ हैं।
    N = {1, 2, 3, 4, 5, 6……….∞}
  2. पूर्ण संख्याएँ
    संख्याओं का वह समूह जिसमें सभी प्राकृतिक संख्याएँ और संख्या शून्य शामिल हैं, पूर्ण संख्याएँ कहलाती हैं। इन्हें गैर-ऋणात्मक पूर्णांक भी कहा जाता है।
    W = {0,1,2,3,4,5,6,7,8,…………..∞}
  3. पूर्णांक
    वे सभी संख्याएँ जिनमें दशमलव स्थान नहीं होता है, पूर्णांक कहलाती हैं।
    Z = {∞…….-3, -2, -1, 0, 1, 2, 3………∞}
    a.  धनात्मक पूर्णांक
    1, 2, 3, 4….. सभी धनात्मक पूर्णांकों का समुच्चय है।
    b. ऋणात्मक पूर्णांक
    −1, −2, −3….. सभी ऋणात्मक पूर्णांकों का समुच्चय है।
    c. अ-धनात्मक और अ-ऋणात्मक पूर्णांक
    0 न तो धनात्मक है और न ही ऋणात्मक।
  4. वास्तविक संख्याएँ
    वे सभी संख्याएँ जिन्हें संख्या रेखा पर दर्शाया जा सकता है, वास्तविक संख्याएँ कहलाती हैं।
  5. परिमेय संख्याएँ
    परिमेय संख्या को a/b के रूप की संख्या के रूप में परिभाषित किया जाता है जहाँ 'a' और 'b' पूर्णांक हैं और b ≠ 0. परिमेय संख्याएँ जो पूर्णांक नहीं हैं, उनके दशमलव मान होंगे। ये मान दो प्रकार के हो सकते हैं
    a. अंत दशमलव भिन्न:
    उदाहरण के लिए: 1551
    = 0.5,12544125
    = 31.25
    b. गैर-अंत दशमलव भिन्न:
    उदाहरण के लिए:196619
    = 3.1666666, 219921
    = 2.33333
  6. अपरिमेय संख्याएँ
    यह एक ऐसी संख्या है जिसे अनुपात रूप (या अंश) के रूप में नहीं लिखा जा सकता है। अपरिमेय संख्याएँ गैर-समापन और गैर-आवधिक भिन्न होती हैं।
    उदाहरण के लिए: 22
     = 1.414
  7. जटिल संख्याएँ
    जटिल संख्याएँ {a+bi} का समूह हैं, जहाँ a और b वास्तविक संख्याएँ हैं और 'i' काल्पनिक इकाई है।
  8. काल्पनिक संख्याएँ
    वह संख्या जो संख्या रेखा पर मौजूद नहीं होती उसे काल्पनिक संख्या कहते हैं।
    उदाहरण के लिए ऋणात्मक संख्याओं का वर्गमूल काल्पनिक संख्याएँ होती हैं। इसे 'i' या 'j' से दर्शाया जाता है।
  9. सम संख्याएँ
    2 से विभाज्य संख्या को सम संख्या कहते हैं।
    उदाहरण के लिए: 2, 6, 8, 14, 18, 246, आदि।
  10. विषम संख्याएँ
    ऐसी संख्याएँ जो 2 से विभाज्य न हों, विषम संख्याएँ कहलाती हैं।
    उदाहरण के लिए: 3, 7, 9, 15, 17, 373, आदि।
  11. अभाज्य संख्याएँ
    1 से बड़ी संख्या को अभाज्य संख्या कहा जाता है, यदि उसके ठीक दो गुणनखंड हों, अर्थात 1 और वह संख्या स्वयं।
    उदाहरण के लिए: 2, 3, 5, 7, 11, 13, 17, आदि।
  12. भाज्य संख्याएँ
    1 से बड़ी संख्याएँ जो अभाज्य नहीं हैं, भाज्य संख्याएँ कहलाती हैं।
    उदाहरण के लिए: 4, 6, 8, 10, आदि।

विभाज्यता नियम

  • 2 से विभाज्यता → वह संख्या जो सम हो या वह संख्या जिसका अंतिम अंक सम हो अर्थात 0, 2, 4, 6 और 8।
  • 3 से विभाज्यता → संख्या के सभी अंकों का योग 3 से विभाज्य होना चाहिए।
  • 4 से विभाज्यता → संख्या के अंतिम दो अंकों से बनी संख्या 4 से विभाज्य होनी चाहिए या 00 होनी चाहिए।
  • 5 से विभाज्यता  → वे संख्याएँ जिनका इकाई स्थान 0 या 5 हो।
  • 6 से विभाज्यता  → एक संख्या जो 2 और 3 दोनों से विभाज्य है।
  • 7 से विभाज्यता → संख्या के अंतिम अंक के दोगुने को शेष अंकों से घटाने पर 7 का गुणज प्राप्त होता है।
  • 8 से विभाज्यता  → संख्या के अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य होनी चाहिए या 000 होनी चाहिए।
  • 9 से विभाज्यता  → संख्या के सभी अंकों का योग 9 से विभाज्य होना चाहिए।
  • 10 से विभाज्यता  → 10 के लिए विभाज्यता नियम बताता है कि कोई भी संख्या जिसका अंतिम अंक 0 है, 10 से विभाज्य है।
  • 11 से विभाज्यता → किसी संख्या के वैकल्पिक अंकों के योग का अंतर 11 से विभाज्य होता है।
  • 12 से विभाज्यता → एक संख्या जो 3 और 4 दोनों से विभाज्य है।
  • 13 से विभाज्यता → किसी भी दी गई संख्या के लिए, यह जाँचने के लिए कि क्या वह 13 से विभाज्य है, हमें संख्या के अंतिम अंक के चार गुना को शेष संख्या में जोड़ना होगा और प्रक्रिया को तब तक दोहराना होगा जब तक आपको दो अंकों की संख्या न मिल जाए। अब जाँचें कि वह दो अंकों की संख्या 13 से विभाज्य है या नहीं। यदि वह विभाज्य है, तो दी गई संख्या 13 से विभाज्य है।
  • 14 से विभाज्यता → 2 और 7 दोनों से विभाज्य संख्या।
  • 16 से विभाज्यता → 16 से विभाज्य अंतिम चार अंक
  • 27 से विभाज्यता → 3 ब्लॉकों का योग (दाएं से बाएं लिया गया) 27 से विभाज्य

विभाज्यता के हल किये गए उदाहरण

प्रश्न 1. क्या 7248 (i) 4 से, (ii) 2 से तथा (iii) 8 से विभाज्य है?
उत्तर: 

(i)  संख्या 7248 के दाईं ओर 48 है जो 4 से पूर्णतः विभाज्य है। जब हम 48 को 4 से विभाजित करते हैं तो हमें 12 प्राप्त होता है।

अतः 7248, 4 से विभाज्य है।

(ii)  संख्या 7248 के इकाई स्थान पर अंक 8 है जो एक सम संख्या है, इसलिए 7248, 2 से विभाज्य है।

(iii)  7248, 8 से विभाज्य है क्योंकि 7248 के सैकड़े के स्थान, दहाई के स्थान तथा इकाई के स्थान पर 248 है जो कि 8 से पूर्णतः विभाज्य है।

प्रश्न 2. एक संख्या 4 और 12 से विभाज्य है। क्या यह आवश्यक है कि यह 48 से भी विभाज्य होगी? अपने उत्तर के समर्थन में एक और उदाहरण दीजिए।
उत्तर: 

48 = 4 × 12 लेकिन 4 और 12 सह-अभाज्य नहीं हैं।

इसलिए यह आवश्यक नहीं है कि संख्या 48 से विभाज्य होगी।

आइये उदाहरण के लिए संख्या 72 पर विचार करें

72 ÷ 4 = 18, अतः 72, 4 से विभाज्य है।

72 ÷ 12 = 6, अतः 72, 12 से विभाज्य है।

लेकिन 72, 48 से विभाज्य नहीं है।

प्रश्न 3. वास्तविक विभाजन के बिना, ज्ञात कीजिए कि क्या 235932 (i) 4 से तथा (ii) 8 से विभाज्य है।
उत्तर: 

(i)  235932 के दाएँ छोर पर अंतिम दो अंकों से बनी संख्या 32 है।

32 ÷ 4 = 8, अर्थात 32, 4 से विभाज्य है।

अतः 235932, 4 से विभाज्य है।

(ii)  235932 के दाएँ छोर पर अंतिम तीन अंकों से बनी संख्या 932 है।

लेकिन 932, 8 से विभाज्य नहीं है।

अतः 235932, 8 से विभाज्य नहीं है।

प्रश्न 4. जाँच करें कि क्या 998, 9 से विभाज्य है?
उत्तर:

नियम के अनुसार, यदि किसी संख्या के अंकों का योग 9 का गुणज है, तो वह संख्या 9 से विभाज्य होगी।
998 के अंकों का योग: 9 + 9 + 8 = 26
26, 9 का गुणज नहीं है
, इसलिए 998, 9 से विभाज्य नहीं है।

प्रश्न 5. जाँच कीजिए कि क्या 1782, 11 से विभाज्य है?
उत्तर:

नियम के अनुसार, यदि किसी संख्या में विषम स्थानों के अंकों का योग और सम स्थानों के अंकों का योग बराबर हो या उनमें 11 से विभाज्य संख्या का अंतर हो, तो वह संख्या 11 से विभाज्य होगी।
1782 में विषम स्थानों के अंकों का योग:
1 + 8 = 9
1782 में सम स्थानों के अंकों का योग:
7 + 2 = 9
1782 में विषम स्थानों के अंकों का योग और सम स्थानों के अंकों का योग बराबर हो।
इसलिए, 1782 11 से विभाज्य है।
Take a Practice Test
Test yourself on topics from Bank Exams exam
 Practice Now
Practice Now

एचसीएफ और एलसीएम

  • दो संख्याओं का HCF * LCM = दो संख्याओं का गुणनफल।
  • a, b, और c को विभाजित करने पर शेषफल x 1 , x 2, और x 3 छोड़ने वाली सबसे बड़ी संख्या (a - x 1 ), (b - x 2 ), और (c - x 3 ) का HCF है ।
  • a, b, तथा c को विभाजित करने पर सबसे बड़ी संख्या (a < b < c) जो प्रत्येक बार समान शेष छोड़े, वह (c - b), (c - a), (b - a) का HCF है।
  • यदि एक संख्या N, X तथा Y से विभाज्य है तथा HCF (X, Y) = 1 है। तो N, X * Y से विभाज्य है।

HCF और LCM के हल किये गए उदाहरण

उदाहरण 1:  96, 36 और 18 का HCF ज्ञात कीजिए।

96 = 2 × 3 × 2 × 2 × 2 × 2
36 = 2 × 3 × 2 × 3
18 = 2 × 3 × 3
इसलिए, 96, 36 और 18 का HCF दी गई संख्याओं में सबसे अधिक सामान्य कारकों का गुणनफल है, अर्थात, 2 × 3 = 6.
दूसरे शब्दों में, 6 सबसे बड़ा संभावित पूर्णांक है, जो 96, 36 और 18 को बिना कोई शेष छोड़े विभाजित कर सकता है।

उदाहरण 2:  42 और 70 का HCF ज्ञात कीजिए।

42 = 3 × 2 × 7
70 = 5 × 2 × 7
अतः, HCF 2 x 7 = 14 है।

उदाहरण 3:  संख्या 144, 630 और 756 का HCF ज्ञात कीजिए।

144 = 2 4 × 3 2
630 =2 × 3 2  × 5 × 7
756 = 2 2 x 3 3 x 7
अतः, 144, 630, 756 का HCF = 2 × 3 2 = 18.

उदाहरण 4:  96, 36 और 18 का LCM ज्ञात कीजिए।

96 = 2 × 2 × 2 × 2 × 2 × 3 = 2 5  × 3 1
36 = 2 x 2 x 3 x 3 = 2 2 x 3 2
18 = 2 x 3 x 3 = 2 1 x 3 2
इसलिए, 96, 36 और 18 का एलसीएम सभी अभाज्य कारकों की उच्चतम शक्तियों का गुणनफल है, अर्थात 2 5 x 3 2  = 32 x 9 = 288।
अर्थात्, 288 सबसे छोटा पूर्णांक है जो बिना कोई शेष छोड़े 96, 36 और 18 से विभाज्य है।

उदाहरण 5:  42 और 70 का LCM ज्ञात कीजिए।

42 = 3 × 2 × 7

70 = 5 × 2 × 7

इसलिए, LCM 2 × 3 × 5 × 7 = 210 है।
अभाज्य गुणनखंड विधि के अलावा, दी गई संख्याओं का LCM ज्ञात करने की एक और विधि है, और इस विधि को दीर्घ विभाजन विधि के रूप में जाना जाता है।  यदि तीन या तीन से अधिक संख्याएँ हैं, तो यह विधि LCM को जल्दी से प्राप्त करने में काफी सहायक है।

उदाहरण 6: 48 और 300 का LCM ज्ञात कीजिए।

यहाँ, हमें 48 और 300 का LCM पता लगाना है।
48 = 2 × 2 × 2 × 2 × 3 = 2 4 × 3 1
300 = 2 × 2 × 3 × 5 × 5 = 2 2 × 3 1 × 5 2
सभी पाई गई संख्याओं को सूचीबद्ध करें, जितनी बार वे आती हैं, सबसे अधिक बार कोई एक दी गई संख्या, और LCM खोजने के लिए उन्हें एक साथ गुणा करें।
इस प्रकार, 2 4  × 3 1 × 5 2 = 1200
इसलिए, 48 और 300 का LCM 1200 है।

उदाहरण 7: 12, 18, 30 का LCM ज्ञात कीजिए।

यहां, हमें 12, 18, 30 का LCM ज्ञात करना है।
अब, उपरोक्त तीन संख्याओं के अभाज्य गुणनखंड ज्ञात करते हैं।
12 = 2 × 2 × 3 = 2 2 × 3 1
18 = 2 × 3 × 3 = 2 1 × 3 2
30 = 2 × 3 × 5 = 2 1 × 3 1  × 5 1
अब, किसी भी दी गई संख्या के लिए जितनी बार वे सबसे अधिक बार आते हैं, सभी अभाज्य संख्याओं को सूचीबद्ध करें और LCM ज्ञात करने के लिए उन्हें एक साथ गुणा करें।
अतः, 2 × 2 × 3 × 3 × 5 = 180
इसके बजाय घातांक का उपयोग करते हुए, प्रत्येक अभाज्य संख्या को उच्चतम घात से गुणा करें।
इस प्रकार, 2 2 × 3 2 × 5 1 = 180
अतः, 12, 18, 30 का लघुत्तम समापवर्त्य 180 है।

एडूरेव टिप:
दो अभाज्य संख्याओं का HCF सदैव 1 होता है।
सह-अभाज्य संख्याओं का HCF सदैव 1 होता है।

The document महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams is a part of the Bank Exams Course Quantitative Aptitude/संख्यात्मक योग्यता.
All you need of Bank Exams at this link: Bank Exams
Are you preparing for Bank Exams Exam? Then you should check out the best video lectures, notes, free mock test series, crash course and much more provided by EduRev. You also get your detailed analysis and report cards along with 24x7 doubt solving for you to excel in Bank Exams exam. So join EduRev now and revolutionise the way you learn!
Sign up for Free Download App for Free
223 docs|265 tests
Join Course for Free

Up next

महत्वपूर्ण सूत्र: संख्या प्रणाली
Doc | 23 pages
परिचय: संख्या प्रणाली
Doc | 56 pages
परिचय: संख्या प्रणाली
Doc | 63 pages

FAQs on महत्वपूर्ण सूत्र: संख्या प्रणाली - Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

1. संख्या प्रणाली क्या होती है और इसके प्रकार क्या हैं?
Ans. संख्या प्रणाली एक ऐसी प्रणाली है जिसका उपयोग संख्याओं को व्यक्त करने और गणना करने के लिए किया जाता है। इसके कई प्रकार हैं, जैसे: 1. दशमलव प्रणाली (Decimal System) - जो 0 से 9 तक के अंकों का उपयोग करती है। 2. द्विआधारी प्रणाली (Binary System) - जो केवल 0 और 1 का उपयोग करती है। 3. अष्टाधारी प्रणाली (Octal System) - जो 0 से 7 तक के अंकों का उपयोग करती है। 4. षष्टाधारी प्रणाली (Hexadecimal System) - जो 0 से 9 और A से F तक के अंकों का उपयोग करती है।
2. संख्या प्रणाली के उपयोग क्या हैं?
Ans. संख्या प्रणाली का उपयोग विभिन्न क्षेत्रों में किया जाता है, जैसे: 1. गणित में संख्याओं की गणना के लिए। 2. कंप्यूटर विज्ञान में डेटा को स्टोर और प्रोसेस करने के लिए। 3. संख्यात्मक विश्लेषण और सांख्यिकी में। 4. इंजीनियरिंग और विज्ञान में माप और गणना के लिए।
3. द्विआधारी प्रणाली कैसे काम करती है?
Ans. द्विआधारी प्रणाली केवल दो अंकों, 0 और 1, का उपयोग करती है। इसमें प्रत्येक अंक का स्थान मान 2 की शक्तियों के अनुसार होता है। उदाहरण के लिए, द्विआधारी संख्या 1011 को समझने के लिए: 1. सबसे दाएं अंक का मान 2^0 होता है, 2. अगला अंक 2^1, 3. फिर 2^2, 4. और सबसे बाएं अंक 2^3 होता है। इस प्रकार, 1011 = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11 (दशमलव में)।
4. संख्या प्रणाली का महत्व क्या है?
Ans. संख्या प्रणाली का महत्व विभिन्न कारणों से है: 1. यह गणितीय और तार्किक सोच को विकसित करती है। 2. यह डेटा को कुशलता से संग्रहीत और प्रसंस्कृत करने की अनुमति देती है। 3. यह विभिन्न वैज्ञानिक और तकनीकी अनुप्रयोगों में आवश्यक है। 4. यह संख्यात्मक समस्याओं को हल करने में मदद करती है।
5. संख्या प्रणाली में परिवर्तन कैसे किया जाता है?
Ans. संख्या प्रणाली में परिवर्तन करने के लिए, एक संख्या को उसकी मूल प्रणाली से दूसरी प्रणाली में परिवर्तित करना होता है। उदाहरण के लिए, दशमलव से द्विआधारी में परिवर्तित करने के लिए, संख्या को 2 से विभाजित करके शेष को रिकॉर्ड करते हैं। इसे तब तक करते हैं जब तक संख्या 0 नहीं हो जाती। फिर शेष को उल्टे क्रम में पढ़ते हैं। इसी तरह, अन्य प्रणालियों के बीच भी परिवर्तन किया जा सकता है।
Related Exams
About this Document
4.91/5 Rating
Mar 29, 2025 Last updated
Document Description: महत्वपूर्ण सूत्र: संख्या प्रणाली for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation. The notes and questions for महत्वपूर्ण सूत्र: संख्या प्रणाली have been prepared according to the Bank Exams exam syllabus. Information about महत्वपूर्ण सूत्र: संख्या प्रणाली covers topics like संख्या प्रणाली क्या है?, बीजगणित में महत्वपूर्ण सूत्र, बीजगणित में सूत्रों का दृश्य प्रतिनिधित्व, संख्या प्रणाली में महत्वपूर्ण सूत्र, संख्याओं के प्रकार, विभाज्यता नियम, एचसीएफ और एलसीएम and महत्वपूर्ण सूत्र: संख्या प्रणाली Example, for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for महत्वपूर्ण सूत्र: संख्या प्रणाली.
Introduction of महत्वपूर्ण सूत्र: संख्या प्रणाली in English is available as part of our Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams & महत्वपूर्ण सूत्र: संख्या प्रणाली in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course. Download more important topics related with notes, lectures and mock test series for Bank Exams Exam by signing up for free. Bank Exams: महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
Description
Full syllabus notes, lecture & questions for महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams - Bank Exams | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude/संख्यात्मक योग्यता | Best notes, free PDF download
Information about महत्वपूर्ण सूत्र: संख्या प्रणाली
In this doc you can find the meaning of महत्वपूर्ण सूत्र: संख्या प्रणाली defined & explained in the simplest way possible. Besides explaining types of महत्वपूर्ण सूत्र: संख्या प्रणाली theory, EduRev gives you an ample number of questions to practice महत्वपूर्ण सूत्र: संख्या प्रणाली tests, examples and also practice Bank Exams tests

Up next

महत्वपूर्ण सूत्र: संख्या प्रणाली
Doc | 23 pages
परिचय: संख्या प्रणाली
Doc | 56 pages
परिचय: संख्या प्रणाली
Doc | 63 pages
Explore Courses for Bank Exams exam
Related Searches

mock tests for examination

,

study material

,

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

,

Objective type Questions

,

video lectures

,

Previous Year Questions with Solutions

,

past year papers

,

Important questions

,

shortcuts and tricks

,

Free

,

Viva Questions

,

Extra Questions

,

Exam

,

MCQs

,

ppt

,

Semester Notes

,

Summary

,

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

,

Sample Paper

,

महत्वपूर्ण सूत्र: संख्या प्रणाली | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams

,

pdf

,

practice quizzes

;
Additional Information about महत्वपूर्ण सूत्र: संख्या प्रणाली for Bank Exams Preparation

महत्वपूर्ण सूत्र: संख्या प्रणाली Free PDF Download

The महत्वपूर्ण सूत्र: संख्या प्रणाली is an invaluable resource that delves deep into the core of the Bank Exams exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the महत्वपूर्ण सूत्र: संख्या प्रणाली now and kickstart your journey towards success in the Bank Exams exam.

Importance of महत्वपूर्ण सूत्र: संख्या प्रणाली

The importance of महत्वपूर्ण सूत्र: संख्या प्रणाली cannot be overstated, especially for Bank Exams aspirants. This document holds the key to success in the Bank Exams exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

महत्वपूर्ण सूत्र: संख्या प्रणाली Notes

महत्वपूर्ण सूत्र: संख्या प्रणाली Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to महत्वपूर्ण सूत्र: संख्या प्रणाली. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, महत्वपूर्ण सूत्र: संख्या प्रणाली Notes on EduRev are your ultimate resource for success.

महत्वपूर्ण सूत्र: संख्या प्रणाली Bank Exams Questions

The "महत्वपूर्ण सूत्र: संख्या प्रणाली Bank Exams Questions" guide is a valuable resource for all aspiring students preparing for the Bank Exams exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study महत्वपूर्ण सूत्र: संख्या प्रणाली on the App

Students of Bank Exams can study महत्वपूर्ण सूत्र: संख्या प्रणाली alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the महत्वपूर्ण सूत्र: संख्या प्रणाली, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of महत्वपूर्ण सूत्र: संख्या प्रणाली is prepared as per the latest Bank Exams syllabus.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup