परिचय: संख्या प्रणाली | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
| Table of contents |

|
| संख्या क्या है? |

|
| संख्याओं का वर्गीकरण |

|
| भाग्यता |

|
| सह-प्राइम या सापेक्ष प्राइम संख्याएँ |

|
| एचसीएफ और एलसीएम के सिद्धांत |

|
| शेषफल |

|
| शून्य की संख्या |

|
| आधार प्रणालियाँ |

|
संख्याएँ हमारे जीवन का एक अभिन्न हिस्सा हैं। इस अध्याय में, हम विभिन्न प्रकार की संख्याओं और उन श्रेणियों के बारे में जानेंगे जिनके अंतर्गत वे आती हैं। यहाँ चर्चा किए गए सिद्धांत आपके MBA प्रवेश परीक्षाओं को पास करने के लिए गणित की आवश्यकताओं को समझने की दिशा में आपका पहला कदम होंगे। जैसे-जैसे हम इस अध्याय में आगे बढ़ेंगे, आप महसूस करेंगे कि आपने पहले से ही कई सिद्धांत स्कूल में सीखे हैं। इससे आपकी आत्मविश्वास और बढ़ेगा।
संख्या क्या है?
संख्या एक गणितीय अवधारणा है जिसका उपयोग गिनने, मापने या चीजों को लेबल करने के लिए किया जाता है। संख्याएँ अंकगणितीय गणनाओं में एक प्रमुख भूमिका निभाती हैं।
- ये विभिन्न प्रकारों में आती हैं, जिनमें प्राकृतिक संख्याएँ, पूर्ण संख्याएँ, तर्कसंगत और अतर्कसंगत संख्याएँ शामिल हैं। यहाँ तक कि 0 भी एक संख्या है, जो एक शून्य मान का प्रतिनिधित्व करती है।
- संख्याएँ 2 द्वारा विभाज्यता के आधार पर सम या विषम के रूप में वर्गीकृत की जा सकती हैं, और गुणांक के अनुसार प्राथमिक या यौगिक के रूप में। सम और विषम का संबंध 2 द्वारा विभाज्यता से है, जबकि प्राथमिक संख्याओं के केवल दो गुणांक होते हैं, और यौगिक संख्याओं के दो से अधिक होते हैं।
- संख्या प्रणालियों में, ये संख्याएँ अंक के रूप में कार्य करती हैं। द्विआधारी प्रणाली में सामान्य अंक 0 और 1 होते हैं, जबकि अन्य प्रणालियाँ 0 से 9 तक के अंकों का उपयोग करती हैं। विभिन्न प्रकार की संख्याओं और उनके प्रणालियों को समझना गणित में आवश्यक है।
संख्याओं का वर्गीकरण
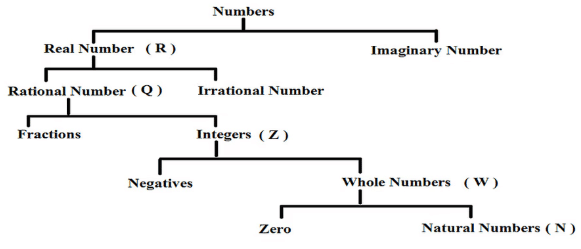
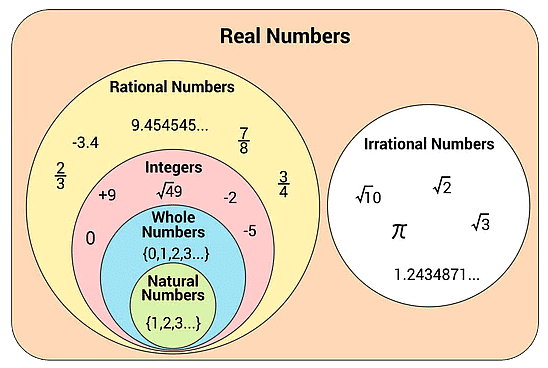
1. वास्तविक संख्याएँ और काल्पनिक संख्याएँ
वास्तविक संख्याएँ तर्कसंगत और अतार्किक संख्याओं के सेट को शामिल करती हैं।
- तर्कसंगत संख्याएँ भिन्नों के रूप में व्यक्त की जा सकती हैं, जैसे कि -3/4 या 5/2, जबकि अतार्किक संख्याएँ, जैसे π (पाई) या √2 (2 का वर्गमूल), को भिन्नों के रूप में दर्शाया नहीं जा सकता और इनकी दशमलव अभिव्यक्तियाँ निरंतर और अपरिवर्तनीय होती हैं।
- वास्तविक संख्याएँ सकारात्मक या नकारात्मक, पूर्ण या भिन्न हो सकती हैं, और ये संख्या रेखा पर स्थित की जा सकती हैं।
- दूसरी ओर, काल्पनिक संख्याएँ काल्पनिक इकाई "i" में शामिल होती हैं, जहाँ i² = -1। जटिल संख्याएँ वास्तविक और काल्पनिक घटकों को मिलाती हैं, जिन्हें a + bi के रूप में लिखा जाता है, जहाँ 'a' और 'b' वास्तविक संख्याएँ होती हैं।
काल्पनिक संख्याओं के उदाहरण में 2i, -3i, और (1 + 4i) शामिल हैं। वास्तविक और काल्पनिक संख्याओं के बीच का संबंध गणित में जटिल विश्लेषण की नींव बनाता है।
2. तार्किक और अतार्किक संख्याएँ
तार्किक संख्याएँ
- तार्किक संख्या एक प्रकार की वास्तविक संख्या है, जो p/q के रूप में होती है जहाँ q शून्य के बराबर नहीं होता। कोई भी भिन्न जिसके गैर-शून्य हर होता है, एक तार्किक संख्या होती है।
- तार्किक संख्याओं के कुछ उदाहरण हैं 1/2, 1/5, 3/4, आदि।
अतार्किक संख्याएँ
- एक संख्या जिसे एक के अनुपात के रूप में व्यक्त नहीं किया जा सकता, उसे अतार्किक संख्याएँ कहा जाता है और इसे "P" प्रतीक द्वारा दर्शाया जाता है। उदाहरण: π (पाई), √2
- प्राकृतिक संख्याओं के सभी वर्ग और घन मूल जो पूर्ण वर्ग या पूर्ण घन नहीं होते, वे अतार्किक होते हैं।
- जोड़ने, घटाने, गुणा करने और विभाजित करने जैसे सभी कार्य जो तार्किक संख्याओं पर लागू होते हैं, वे अतार्किक संख्याओं पर भी लागू होते हैं।
- जब एक सूत्र में एक तार्किक और एक अतार्किक संख्या दोनों शामिल होते हैं, तो उन्हें समाधान के दौरान एक साथ रहना चाहिए। दूसरे शब्दों में, जब एक अतार्किक संख्या प्रकट होती है, तो इसे केवल तभी समाप्त किया जा सकता है जब इसे एक ही अतार्किक संख्या से गुणा या विभाजित किया जाए।
3. पूर्णांक (Z)
वह सेट जिसमें सभी पूर्णांक और उनके नकारात्मक मान शामिल होते हैं, उसे पूर्णांकों का सेट कहा जाता है। इसे Z से दर्शाया जाता है, और Z = {- ∞, … - 3, - 2, - 1, 0, 1, 2, 3, ……. ∞}।
- इन्हें आगे निम्नलिखित वर्गों में वर्गीकृत किया जाता है: नकारात्मक पूर्णांक, तटस्थ पूर्णांक और सकारात्मक पूर्णांक। (a) नकारात्मक पूर्णांक (Z-) वे सभी पूर्णांक जो शून्य से छोटे होते हैं, उन्हें नकारात्मक पूर्णांक कहा जाता है। Z− = {- 1, - 2, - 3…- ∞ } (b) तटस्थ पूर्णांक (Z0) शून्य एकमात्र पूर्णांक है जो न तो नकारात्मक है और न ही सकारात्मक, और इसे तटस्थ पूर्णांक कहा जाता है। (c) सकारात्मक पूर्णांक (Z+) वे सभी पूर्णांक जो शून्य से बड़े होते हैं, उन्हें सकारात्मक पूर्णांक कहा जाता है। Z+ = {1, 2, 3, …….., ∞ }।
4. पूर्ण संख्याएँ
संख्याओं का वह समूह जिसमें सभी प्राकृतिक संख्याएँ और शून्य शामिल हैं, उसे पूर्ण संख्याएँ कहा जाता है।
पूर्ण संख्याओं को गैर-नकारात्मक पूर्णांक भी कहा जाता है।
5. प्राकृतिक संख्याएँ (N)
संख्याएँ 1, 2, 3, 4, 5… को प्राकृतिक संख्याएँ कहा जाता है। प्राकृतिक संख्याओं का समूह N द्वारा प्रदर्शित किया जाता है।
- सभी सकारात्मक पूर्णांक प्राकृतिक संख्याएँ हैं, इसलिए, यहाँ अनंत प्राकृतिक संख्याएँ हैं।
- इसलिए, N = {1, 2, 3, 4…}। प्राकृतिक संख्याएँ और भी वर्गीकृत की जाती हैं जैसे कि सम, विषम, अभाज्य आदि।
- पूर्ण संख्याएँ (W): सभी प्राकृतिक संख्याएँ और ‘0’ मिलाकर पूर्ण संख्याएँ कहलाती हैं। पूर्ण संख्याओं का समूह W द्वारा प्रदर्शित किया जाता है, और W = {0, 1, 2, 3, ……} है।
6. सम और विषम संख्याएँ
2 से विभाज्य सभी संख्याओं को सम संख्याएँ कहा जाता है।
उदाहरण: 2, 4, 6, 8, 10.…
सम संख्याएँ 2n के रूप में व्यक्त की जा सकती हैं, जहाँ n एक पूर्णांक है। इस प्रकार 0, -2, −6 आदि भी सम संख्याएँ हैं।
2 से विभाज्य नहीं होने वाली सभी संख्याओं को विषम संख्याएँ कहा जाता है।
विषम संख्याएँ (2n + 1) के रूप में व्यक्त की जा सकती हैं जहाँ n एक पूर्णांक है।
उदाहरण:
-1, −3, −5…
1, 3, 5, 7, 9…
7. अभाज्य संख्याएँ
एक प्राकृतिक संख्या जिसे केवल स्वयं और एक से विभाजित किया जा सके, उसे अभाज्य संख्या कहा जाता है।
उदाहरण: 2, 3, 5, 7, 11, 13, 17, 19 …
इसके विपरीत, एक संख्या जिसे दो से अधिक कारक होते हैं, उसे सम Composite संख्या कहा जाता है।
अभाज्य संख्याओं के बारे में महत्वपूर्ण अवलोकन
- 3 से बड़ी कोई भी अभाज्य संख्या 6 से विभाजित होने पर या तो 1 या 5 शेष छोड़ती है।
- इसलिए, एक अभाज्य संख्या को 6K ± 1 या 6K ± 5 के रूप में व्यक्त किया जा सकता है।
- लेकिन इस अवलोकन का विपरीत सत्य नहीं है, कि 6 से विभाजित होने पर 1 या 5 शेष छोड़ने वाली संख्या अभाज्य संख्या नहीं हो सकती। उदाहरण: 25, 35 आदि।
अभाज्य संख्याओं की कुछ विशेषताएँ
- सबसे छोटी अभाज्य संख्या 2 है।
- संख्या 2 ही एकमात्र सम अभाज्य संख्या है।
- सबसे छोटी विषम अभाज्य संख्या 3 है।
- जब एक अभाज्य संख्या p ≥ 5 को 6 से विभाजित किया जाता है, तो शेष 1 या 5 होता है।
- एक अभाज्य संख्या p ≥ 5 का वर्ग 24 से विभाजित होने पर शेष 1 होता है।
- अभाज्य संख्याओं के लिए, p > 3, p² - 1 24 से विभाज्य है।
- एक अभाज्य संख्या p ≥ 5 के वर्ग को 12 से विभाजित करने पर शेष 1 होता है।
- यदि a और b कोई भी दो विषम अभाज्य संख्याएँ हैं, तो a2 - b2 और a2 + b2 दोनों Composite संख्याएँ हैं।
कैसे जांचें कि कोई संख्या अभाज्य है या नहीं
किसी संख्या N के अभाज्य होने की जाँच करने के लिए निम्नलिखित प्रक्रिया अपनाएँ:
- संख्या का वर्गमूल लें।
- समीपतम उच्च पूर्णांक में वर्गमूल को गोल करें। इस संख्या को z कहें।
- संख्या N की z से छोटी सभी अभाज्य संख्याओं द्वारा विभाज्यता की जाँच करें।
- यदि z के मान से नीचे कोई अभाज्य संख्या N को विभाजित नहीं करती है, तो संख्या N अभाज्य होगी।
- यदि किसी संख्या का कोई अभाज्य कारक उसके वर्गमूल के बराबर या उससे कम नहीं है, तो वह संख्या अभाज्य संख्या है।
उदाहरण के लिए:
√239 का मान 15 से 16 के बीच है। इसलिए, z का मान 16 लें।
16 से छोटी अभाज्य संख्याएँ 2, 3, 5, 7, 11 और 13 हैं। 239 इनमें से किसी से भी विभाजित नहीं होती।
इसलिए, आप निष्कर्ष निकाल सकते हैं कि 239 एक अभाज्य संख्या है।
अभाज्य संख्याएँ खोजने का त्वरित तरीका
- अधिकांश प्रतिस्पर्धात्मक परीक्षाओं में, यह जाँचना कि कोई संख्या अभाज्य है या नहीं, अक्सर 100 से 200 के बीच 2-अंकीय या 3-अंकीय संख्याओं पर केंद्रित होता है।
- आपको 5 के द्वारा विभाज्यता की जाँच करने की आवश्यकता नहीं है क्योंकि इसे पहचानना आसान है; 5 से विभाजित होने वाली संख्याएँ 0 या 5 पर समाप्त होती हैं।
- इसलिए, ऐसी संख्या को अभाज्य के रूप में पहचानने में गलती करने का कोई जोखिम नहीं है जैसे कि 45।
- इसलिए, जब किसी संख्या के square root के नीचे अभाज्य संख्याओं की जाँच की जाती है, तो 5 को परीक्षण से बाहर रखा जाता है।
- सभी सम संख्याओं (2 को छोड़कर, जो एक अभाज्य संख्या है) को भी इसी तरह बाहर रखा जाता है।
49 से नीचे की संख्याओं की अभाज्यता की जाँच
- 49 से नीचे की संख्याओं के लिए, आपको केवल यह जाँचने की आवश्यकता है कि संख्या 3 से विभाज्य है या नहीं। चूंकि 47 3 से विभाजित नहीं होता, यह एक अभाज्य संख्या है।
- हम 2, 5 या 7 (7 का वर्ग 49 से बड़ा है) द्वारा विभाज्यता की जाँच नहीं कर रहे हैं।
49 से ऊपर और 121 से नीचे की संख्याओं की अभाज्यता की जाँच
- यह 3 और 7 द्वारा विभाज्यता की जाँच करके किया जा सकता है।
- हालांकि, यदि आप याद रखें कि 77, 91, और 119 अभाज्य नहीं हैं, तो आप केवल 3 से विभाज्यता की जाँच करके 121 से नीचे की अभाज्य संख्याओं की पहचान कर सकते हैं।
- यह इसलिए है क्योंकि 49 और 121 के बीच जो विषम संख्याएँ 7 से विभाजित होती हैं, वे 63, 77, 91, 105, और 119 हैं। इनमें से केवल 91 और 119 को गलती से अभाज्य के रूप में देखा जा सकता है। लेकिन 77 और 105 स्पष्ट रूप से अभाज्य नहीं हैं।
- तो, 49 और 121 के बीच की संख्याओं के लिए, केवल यह जाँचें कि वे 3 से विभाजित हैं या नहीं। यदि वे नहीं हैं और वे 91 या 119 नहीं हैं, तो वे अभाज्य संख्याएँ हैं। उदाहरण के लिए, 61 अभाज्य है क्योंकि यह 3 से विभाजित नहीं है और न ही यह 91 या 119 है।
संख्या के प्रमुख होने की जांच (121 से ऊपर और 169 से नीचे के लिए)
- इसकी जांच 3, 7 और 11 द्वारा विभाज्यता परीक्षण करके की जा सकती है।
- हालांकि, यदि आप याद रखें कि 133, 143, और 161 प्रमुख नहीं हैं, तो आप 121 और 169 के बीच प्रमुख संख्याओं की पहचान केवल यह जांचकर कर सकते हैं कि क्या वे 3 से विभाज्य हैं।
- यहाँ कारण है: 121 और 169 के बीच की वे विषम संख्याएँ जो 7 या 11 से विभाज्य हैं, वे हैं 133, 143, 147, 161, और 165। इनमें से, 133, 143, और 161 को प्रमुख समझा जा सकता है यदि आप 7 या 11 द्वारा विभाज्यता की जांच नहीं करते हैं। संख्या 147 को 3 द्वारा विभाज्यता की जांच करते समय प्रमुख नहीं दिखेगी, और आप आसानी से बता सकते हैं कि 165 प्रमुख नहीं है।
- इसलिए, 121 और 169 के बीच की संख्याओं के लिए, आप केवल 3 द्वारा विभाज्यता की जांच करके यह पता कर सकते हैं कि कोई संख्या प्रमुख है या नहीं।
- उदाहरण के लिए, 149 प्रमुख है क्योंकि यह 3 से विभाज्य नहीं है और 133, 143, या 161 में से कोई भी नहीं है।

जानना आवश्यक
1 से 25 ⇒ 9 प्रमुख संख्याएँ
1 से 50 ⇒ 15 प्रमुख संख्याएँ
1 से 100 ⇒ 25 प्रमुख संख्याएँ
1 से 200 ⇒ 45 प्रमुख संख्याएँ
उदाहरण: यदि a, a + 2, a + 4 लगातार प्रमुख संख्याएँ हैं। तो 'a' के कितने समाधान हो सकते हैं?
(a) एक
(b) दो
(c) तीन
(d) तीन से अधिक
उत्तर: सही उत्तर विकल्प (a) है
- कोई भी सम मान 'a' इस शर्त को संतुष्ट नहीं करता। इसलिए 'a' विषम होना चाहिए।
- लेकिन तीन लगातार विषम संख्याओं में से कम से कम एक संख्या 3 का गुणांक होती है।
- तो, एकमात्र संभावना 'a' = 3 है और संख्याएँ हैं 3, 5, 7।
8. यौगिक संख्याएँ
एक यौगिक संख्या में इसके स्वयं और एक के अलावा अन्य गुणांक होते हैं।
- प्रत्येक यौगिक संख्या n को इसके प्रमुख गुणांकों में विभाजित किया जा सकता है।
- इसे इस प्रकार लिखा जा सकता है: n = p1m . p2n ... pks, जहाँ p1, p2 ... pk प्रमुख गुणांक हैं और m, n ... k प्राकृतिक संख्याएँ हैं।
- उदाहरण के लिए, 24 = 23 . 3, और 84 = 7 . 3 . 22
- यौगिक संख्या का यह प्रतिनिधित्व यौगिक संख्या का मानक रूप के रूप में जाना जाता है।
उदाहरण: 8, 72, 39, आदि।
- इस तथ्य के आधार पर कि एक संख्या जिसमें दो से अधिक गुणांक होते हैं वह यौगिक होती है, 1 से 50 तक केवल 34 यौगिक हैं और 51 से 100 तक 40 यौगिक हैं।
नोट: 1 न तो एक प्रमुख संख्या है और न ही एक यौगिक संख्या।
9. पूर्ण संख्याएँ
किसी संख्या को पूर्ण संख्या कहा जाता है यदि इसके सभी गुणांक (खुद को छोड़कर लेकिन 1 को शामिल करते हुए) का योग खुद संख्या के बराबर हो या संख्या के सभी संभावित गुणांकों का योग संख्या के दोगुने के बराबर हो।
- यदि किसी पूर्ण संख्या के 1 को छोड़कर सभी गुणांक लिखे जाएँ और उनके व्युत्क्रम जोड़े जाएँ, तो परिणाम हमेशा एक (Unity) होता है।
- उदाहरण: 6 एक पूर्ण संख्या है क्योंकि 6 के गुणांक, अर्थात् 1, 2 और 3, का योग खुद संख्या 6 के बराबर है।
इसके अलावा, 1/6 + 1/3 + 1/2 = (1 + 2 + 3/6) = 6/6 = 1 (Unity)
अन्य पूर्ण संख्याओं के उदाहरण 28, 496, 8128 आदि हैं।
अब तक 27 पूर्ण संख्याएँ खोजी जा चुकी हैं।
10. भिन्न
भिन्न एक इकाई के भाग या भागों को दर्शाता है।
भिन्नों के कई प्रकार होते हैं:
- सामान्य भिन्न: भिन्न जिनका हर (denominator) 10 या उसके गुणज (multiple) नहीं होते। उदाहरण: 2/3, 17/18
- दशमलव भिन्न: भिन्न जिनका हर 10 या 10 के गुणज होते हैं।
- सही भिन्न: इसमें अंश (numerator) हर से कम होता है। उदाहरण: 2/10, 6/7, 8/9 आदि। इसलिए इसका मान 1 से कम होता है।
- असमान भिन्न: इसमें अंश हर से अधिक होता है। उदाहरण: 10/2, 7/6, 8/7 आदि। इसलिए इसका मान 1 से अधिक होता है।
- मिश्रित भिन्न: जब एक असमान भिन्न को एक पूर्णांक और एक सही भिन्न के रूप में लिखा जाता है, तो इसे मिश्रित भिन्न कहते हैं। उदाहरण: 7/3 को 2 + 1/3 = 2(1/3) के रूप में लिखा जा सकता है।
11. दशमलव संख्या
एक दशमलव संख्या वह संख्या है जिसमें एक दशमलव बिंदु होता है। उदाहरण के लिए, 1.5, 3.22, 829.234
- जब हम किसी संख्या को दूसरी संख्या से विभाजित करते हैं, तो हमेंसमाप्त दशमलव भिन्न या असमाप्त दशमलव भिन्न प्राप्त होती है।
- समाप्त दशमलव भिन्न वे संख्याएँ हैं जिनमें दशमलव बिंदु के बाद निश्चित या सीमित संख्या के अंक होते हैं।
- असमाप्त दशमलव भिन्न को दशमलव के बाद अंकों की आवृत्ति के आधार पर निम्नलिखित प्रकारों में वर्गीकृत किया जा सकता है:
1. शुद्ध पुनरावर्ती दशमलव: एक दशमलव जिसमें दशमलव बिंदु के बाद सभी अंक दोहराते हैं, उसे शुद्ध पुनरावर्ती दशमलव कहा जाता है।
उदाहरण: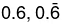 शुद्ध पुनरावर्ती दशमलव के उदाहरण हैं।
शुद्ध पुनरावर्ती दशमलव के उदाहरण हैं। 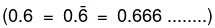
2. मिश्रित पुनरावर्ती दशमलव: एक दशमलव जिसमें कुछ अंक दोहराते हैं और कुछ नहीं, उसे मिश्रित पुनरावर्ती दशमलव कहा जाता है।
उदाहरण: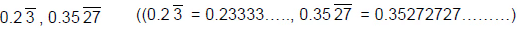
3. गैर-पुनरावर्ती दशमलव: एक दशमलव संख्या जिसमें अंक किसी पैटर्न में नहीं दोहराते हैं, उसे गैर-पुनरावर्ती दशमलव कहा जाता है और इसे असंगत संख्याएँ कहा जाता है।
पुनरावर्ती भिन्न को दशमलव में परिवर्तित करना:
सभी पुनरावर्ती दशमलवों को भिन्नों में परिवर्तित किया जा सकता है। कुछ सामान्य प्रकार हैं 0.33….., 0.1232323…, 5.33…., 14.23636363…. आदि।
(क) शुद्ध पुनरावर्ती से भिन्नों में
फंडा 1: यदि संख्या 0. ababab……. के रूप में है, तो दोहराते अंकों को जितनी बार दोहराया गया है, उतनी 9 से विभाजित करें।
उदाहरण: 0.363636...= 36/99 = 4/11
(ख) मिश्रित पुनरावर्ती से भिन्नों में
फंडा 2: यदि N = 0. abcbcbc…. तो N = abc - a/990 = दोहराए गए एवं गैर-दोहराए गए अंकों का अंतर/ जितनी बार दोहराए गए अंकों की संख्या उतनी 9 के बाद जितने गैर-दोहराए गए अंक हैं।
उदाहरण: 0.25757...= 257 - 2/990 = 255/990 = 17/66
फंडा 3: यदि N = a. bcbc…. तो
लिखें N = a + 0. bcbc…. पहले फंडा 1 के अनुसार आगे बढ़ें।
उदाहरण: 5.3636… = 5 + 0.3636… = 5 + 36/99 = 59/11
12. संख्यात्मक रेखा का सिद्धांत
संख्यात्मक रेखा एक सीधी रेखा है जो दोनों दिशाओं में अनंत विस्तार करती है, बाईं ओर नकारात्मक अनंत और दाईं ओर सकारात्मक अनंत है।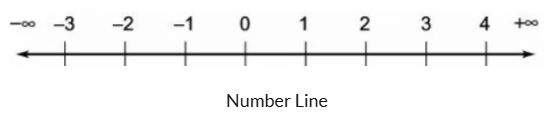
- संख्यात्मक रेखा पर किसी भी दो बिंदुओं के बीच की दूरी घटाने से प्राप्त की जाती है, जिसमें निम्न मान को उच्च मान से घटाया जाता है।
- एक और तरीका यह है कि छोटे संख्या से शुरू करें और देखें कि बड़े संख्या तक पहुँचने के लिए आपको कितना जोड़ना है।
- उदाहरण के लिए: 7 और –4 के बीच की दूरी 7 – (–4) = 11 है।
भाग्यता
- जैसा कि नाम से स्पष्ट है, भाग्यता परीक्षण या गणित में विभाजन नियम यह मदद करते हैं कि कोई संख्या किसी अन्य संख्या द्वारा विभाज्य है या नहीं, बिना वास्तविक विभाजन विधि का उपयोग किए।
- यदि संख्या x को संख्या y द्वारा बिना कोई शेष के विभाजित किया जा सकता है, तो x को y द्वारा भाग्यशाली माना जाता है।
- सामान्यतः, जब एक पूर्णांक 𝐼 को एक प्राकृतिक संख्या 𝑁 द्वारा विभाजित किया जाता है, तो एक अद्वितीय संख्या जोड़ी 𝑄 (उपभाज्य) और 𝑅 (शेष) होती है। इसे इस प्रकार व्यक्त किया जा सकता है:
𝐼 = 𝑄𝑁 + 𝑅 - किसी भी पूर्णांक 𝐼 और किसी भी प्राकृतिक संख्या 𝑁 के लिए, संख्याओं 𝑄 और 𝑅 की एक अद्वितीय जोड़ी होती है जैसे कि 𝐼 =𝑄𝑁 + 𝑅, जहाँ 𝑄 एक पूर्णांक है, 𝑁 एक प्राकृतिक संख्या (या शून्य) है, और 0 ≤ 𝑅 < 𝑁 (जिसका अर्थ है कि शेष 𝑁 से कम एक पूर्ण संख्या होनी चाहिए)। यदि शेष 𝑅 शून्य है, तो हम कहते हैं कि 𝐼 𝑁 से विभाज्य है
नोट: जब हम एक नकारात्मक संख्या को एक प्राकृतिक संख्या N द्वारा विभाजित करते हैं, तो शेष हमेशा नकारात्मक नहीं होता। उदाहरण के लिए, जब हम –32 को 7 से विभाजित करते हैं, तो शेष वास्तव में +3 होता है, न कि –4, जो आश्चर्यजनक हो सकता है। इसका कारण यह है कि शेष हमेशा नकारात्मक नहीं होता। इसलिए, जब हम –32 को 7 से विभाजित करते हैं, तो उपभाज्य –5 होता है और शेष +3 होता है।
भाग होने के प्रमेय

भाग होने के नियम
1.1 का भाग होने का नियम
- प्रत्येक संख्या 1 से भाग होता है। 1 के लिए भाग होने का नियम कोई शर्त नहीं रखता। कोई भी संख्या जब 1 से विभाजित की जाती है, तो वही संख्या प्राप्त होती है, चाहे वह संख्या कितनी भी बड़ी हो।
- उदाहरण: 3 1 से भाग होता है और 3000 भी पूरी तरह से 1 से भाग होता है।
2.2 का भाग होने का नियम
- यदि कोई संख्या सम है या उस संख्या का अंतिम अंक सम है यानी 2, 4, 6, 8, जिसमें 0 भी शामिल है, तो वह हमेशा 2 से पूरी तरह भाग होती है।
- उदाहरण: 508 एक सम संख्या है और 2 से भाग होती है लेकिन 509 नहीं है। यह चेक करने की प्रक्रिया इस तरह है:
⇒ संख्या 508 पर विचार करें
⇒ केवल अंतिम अंक 8 को लें और उसे 2 से विभाजित करें
⇒ यदि अंतिम अंक 8, 2 से भाग होता है तो संख्या 508 भी 2 से भाग होती है।
3.3 के लिए भाग होने के नियम
- 3 के लिए भाग होने का नियम कहता है कि यदि किसी संख्या के अंकों का योग 3 से भाग होता है, तो वह संख्या पूरी तरह से 3 से भाग होती है।
- उदाहरण: एक संख्या पर विचार करें, 308। यह चेक करने के लिए कि 308 3 से भाग होता है या नहीं, अंकों का योग लें (यानी 3+0+8= 11)। अब चेक करें कि क्या योग 3 से भाग होता है। यदि योग 3 का गुणांक है, तो मूल संख्या भी 3 से भाग होती है। यहाँ, चूंकि 11 3 से भाग नहीं होता, 308 भी 3 से भाग नहीं होता।
- इसी प्रकार, 516 पूरी तरह से 3 से भाग होता है क्योंकि इसके अंकों का योग यानी 5+1+6=12, 3 का गुणांक है।
4.4 का भाग होने का नियम
- यदि किसी संख्या के अंतिम दो अंक 4 से भाग होते हैं, तो वह संख्या 4 का गुणांक होती है और पूरी तरह से 4 से भाग होती है।
- उदाहरण: संख्या 2308 लें। अंतिम दो अंकों पर विचार करें यानी 08। चूंकि 08 4 से भाग होता है, मूल संख्या 2308 भी 4 से भाग होती है।
5.5 का भाग होने का नियम
- संख्याएँ, जिनका अंतिम अंक 0 या 5 है, वे हमेशा 5 से भाग होती हैं।
- उदाहरण: 10, 10000, 10000005, 595, 396524850, आदि।
6.6 का भाग होने का नियम
- संख्याएँ जो 2 और 3 दोनों से भाग होती हैं, वे 6 से भी भाग होती हैं। यानी, यदि दी गई संख्या का अंतिम अंक सम है और उसके अंकों का योग 3 का गुणांक है, तो दी गई संख्या भी 6 का गुणांक होती है।
- उदाहरण: 630, संख्या 2 से भाग होती है क्योंकि अंतिम अंक 0 है। अंकों का योग 6+3+0 = 9 है, जो 3 से भी भाग होता है। इस प्रकार, 630 6 से भाग होती है।
7.7 के लिए भाग होने के नियम
7 से भाग होने का नियम थोड़ा जटिल है, जिसे नीचे दिए गए चरणों द्वारा समझा जा सकता है:
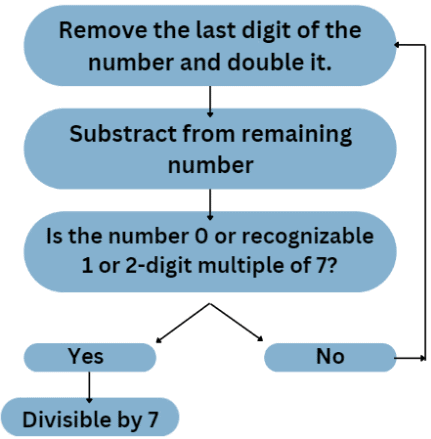
उदाहरण: क्या 1073 7 से भाग होता है?
- प्रस्तावित नियम से 3 को संख्या से हटा दें और उसे दो गुणा करें, जो 6 बनता है।
- शेष संख्या 107 बन जाती है, तो 107-6 = 101।
- एक बार फिर प्रक्रिया को दोहराते हैं, हमें मिलता है 1 x 2 = 2।
- शेष संख्या 10 – 2 = 8।
- चूंकि 8 7 से भाग नहीं होता, इसलिए संख्या 1073 7 से भाग नहीं होती।
8.8 का भाग होने का नियम
- यदि किसी संख्या के अंतिम तीन अंक 8 से भाग होते हैं, तो वह संख्या पूरी तरह से 8 से भाग होती है।
- उदाहरण: संख्या 24344 लें।
अंतिम तीन अंकों पर विचार करें यानी 344।
चूंकि 344 8 से भाग होता है, मूल संख्या 24344 भी 8 से भाग होती है।
9.9 का भाग होने का नियम
- 9 से भाग होने का नियम 3 के भाग होने के नियम के समान है। यानी, यदि संख्या के अंकों का योग 9 से भाग होता है, तो संख्या भी 9 से भाग होती है।
- उदाहरण: 78532 पर विचार करें, चूंकि इसके अंकों का योग (7+8+5+3+2) 25 है, जो 9 से भाग नहीं होता, इसलिए 78532 9 से भाग नहीं होता।
10.10 का भाग होने का नियम
- 10 के लिए भाग होने का नियम कहता है कि कोई भी संख्या जिसका अंतिम अंक 0 है, वह 10 से भाग होती है।
- उदाहरण: 10, 20, 30, 1000, 5000, 60000, आदि।
11.11 के लिए भाग होने के नियम
यदि किसी संख्या के वैकल्पिक अंकों के योग का अंतर 11 से भाग होता है, तो वह संख्या पूरी तरह से 11 से भाग होती है।
जैसे कि 2143 संख्या को 11 से भाग होने की जांच करने के लिए, नीचे दी गई प्रक्रिया का अनुसरण करें:
- वैकल्पिक अंकों को समूहित करें यानी जो अंक विषम स्थानों में हैं उन्हें एक साथ और जो अंक समान स्थानों में हैं उन्हें एक साथ। यहाँ 24 और 13 दो समूह हैं।
- प्रत्येक समूह के अंकों का योग लें यानी 2+4=6 और 1+3= 4
- अब योग का अंतर निकालें; 6-4=2
- यदि अंतर 11 से भाग होता है, तो मूल संख्या भी 11 से भाग होती है। यहाँ 2 अंतर है जो 11 से भाग नहीं होता।
- इसलिए, 2143 11 से भाग नहीं होता।
12.12 का विभाजन नियम
- यदि कोई संख्या 3 और 4 दोनों से विभाज्य है, तो वह संख्या 12 से भी बिल्कुल विभाज्य है।
- उदाहरण: 5864
⇒ अंकों का योग = 5 + 8 + 6 + 4 = 23 (3 का गुणज नहीं)
⇒ अंतिम दो अंक = 64 (4 से विभाज्य)
⇒ दी गई संख्या 5846, 4 से विभाज्य है लेकिन 3 से नहीं; इसलिए, यह 12 से विभाज्य नहीं है।
13.13 के लिए विभाजन नियम
- किसी भी संख्या के लिए, यह जांचने के लिए कि क्या यह 13 से विभाज्य है, हमें संख्या के अंतिम अंक को चार गुना कर के शेष संख्या में जोड़ना होगा और इस प्रक्रिया को दो अंकों की संख्या प्राप्त होने तक दोहराना होगा।
- अब जांचें कि क्या वह दो अंकों की संख्या 13 से विभाज्य है या नहीं। यदि यह विभाज्य है, तो दी गई संख्या 13 से विभाज्य है।
- उदाहरण: 2795 ⇒ 279 + (5 x 4)
⇒ 279 + (20) ⇒ 299 ⇒ 29 + (9 x 4) = 29 + 36 = 65
संख्या 65, 13 से विभाज्य है, 13 x 5 = 65.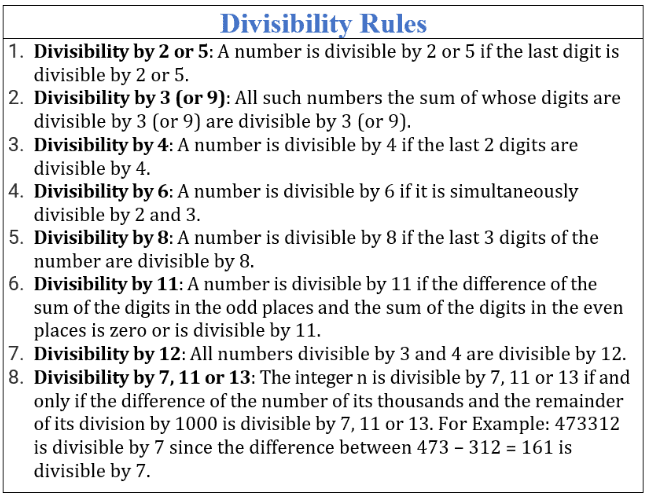
संख्याओं के गुण
- हर संख्या केपांचवें घात में इकाई का अंक वही होता है जो उसके पहले घात में होता है। इसलिए, एक सामान्य विधि यह है कि दिए गए घात को 4 से विभाजित करें, शेष घात ज्ञात करें और उस संख्या में इकाई का अंक जांचें। यह शॉर्टकट इसलिए लागू किया जा सकता है क्योंकि आपको हमेशा वही इकाई का अंक मिलेगा।
- किसी संख्या के फैक्ट्रियल के अंत में शून्यों की संख्या ज्ञात करने के लिए, आपको संख्या को 5 से विभाजित करना चाहिए, प्राप्त भाग को फिर से 5 से विभाजित करें और इसी तरह तब तक जारी रखें जब तक अंतिम भाग 5 से छोटा न हो जाए। सभी भागों का योग 5 की संख्या है, जो तब दी गई संख्या में शून्यों की संख्या बन जाती है।
- किसी संख्या की डिजिटल जड़ अंक का योग है, बार-बार, जब तक यह एक एकल अंक संख्या नहीं बन जाती। उदाहरण के लिए, 87984 की डिजिटल जड़ होगी 8 + 7 + 9 + 8 + 4 ⇒ 36 = 3 + 6 ⇒ 9।
- जब यूलेर संख्या का उपयोग किया जाता है और भाज्य और भाजक सह-प्राइम होते हैं, तो शेष प्रश्न बहुत आसान हो जाते हैं।
- तीन लगातार प्राकृतिक संख्याओं का गुणनफल6 से विभाज्य होता है।
उदाहरण के लिए, मान लीजिए n, n+1 और n+2 तीन लगातार प्राकृतिक संख्याएँ हैं और P(n) उनका गुणनफल है।
तब, P(n)=n(n+1)(n+2) है।
हमारे पास,
P(1)=1×2×3=6, जो 3 और 6 से विभाज्य है।
P(2)=2×3×4=24, जो 3, 8 और 6 से विभाज्य है।
P(3)=3×4×5=60, जो 3 और 6 से विभाज्य है।
P(4)=4×5×6=120, जो 3, 8 और 6 से विभाज्य है।
इसलिए, P(n) सभी n∈ N के लिए 3 और 6 से विभाज्य है। - तीन लगातार प्राकृतिक संख्याओं का गुणनफल, जिनमें से पहली सम संख्या है, 24 से विभाज्य होती है।
- एक दो-अंक संख्या और उसकी अंकों को उलटकर बनायी गई संख्या का योग 11 से विभाज्य होता है।
- xn - yn = (x + y) (xn-1 - xn-2.y + ... yn-1) जब n सम हो। इसलिए, जब n सम होता है, xn - yn x + y से विभाज्य होता है। उदाहरण: 72 - 32 = 40, जो 10 (7+3) से विभाज्य है।
- xn - yn = (x - y) (xn-1 + xn-2.y + ... yn-1) दोनों विषम और सम n के लिए। इसलिए, xn - yn x - y से विभाज्य होता है। उदाहरण: 94 - 24 = 6545, जो 7 (9 – 2) से विभाज्य है।
संख्याएँ का निरपेक्ष मान
- किसी संख्या का मोड्यूलस उस संख्या का निरपेक्ष मान है या हम कह सकते हैं कि यह संख्या का मूल से दूरी है। किसी संख्या का निरपेक्ष मान इस प्रकार परिभाषित किया गया है:
|a| = a, यदि a ≥ 0
= - a, यदि a ≤ 0
|a| को मोड्यूलस (MODULUS) के रूप में पढ़ा जाता है। - उदाहरण: |79| = 79 एवं | - 45| = - (- 45) = 45
इसके अलावा, | x - 3 | = x - 3, यदि x ≥ 3
= 3 - x, यदि x <3.
समाधान किए गए उदाहरण
उदाहरण 1. N = (18n2 + 9n + 8)/n; जहाँ N पूर्णांक है। N के कितने पूर्णांक समाधान संभव हैं?
उत्तर: दी गई अभिव्यक्ति को इस प्रकार तोड़ा जा सकता है: 18n2/n + 9n/n + 8/n। इससे हमें प्राप्त होता है: 18n + 9 + 8/n।
- अब हम देख सकते हैं कि चाहे ‘n’ का कोई भी मान हो, 18n + 9 हमेशा एक पूर्णांक मान देगा। इसलिए, यह अब 8/n पर निर्भर करता है ⇒ n किसी भी पूर्णांक मान को ले सकता है, जो 8 का गुणांक हो।
- जो पूर्णांक इस शर्त को पूरा करेंगे वे हैं ±1, ±2, ±8, ±4। इस प्रकार, कुल मिलाकर, n 8 मान ले सकता है।
उदाहरण 2. N = 960। N के कुल गुणांकों की संख्या ज्ञात करें।
उत्तर:
- एक समग्र संख्या के गुणांक की संख्या: यदि D एक समग्र संख्या है, जो इस रूप में है D = ap × bq × cr, जहाँ a, b, c अभाज्य हैं, तो D के गुणांकों की संख्या, जिसे n से दर्शाया गया है, इस प्रकार दी जाती है: n = (p+1)(q+1)(r +1)।
- इसी प्रकार, 960 को अभाज्य गुणकों में विभाजित करने के बाद: 26 × 31 × 51, हम गुणांकों की कुल संख्या की गणना कर सकते हैं: (6+1)(1+1)(1+1) = 28।
उदाहरण 3. निम्नलिखित अभिव्यक्ति का इकाई अंक ज्ञात करें: (123)34 × (876)456 × (45)86.
उत्तर: जब भी एक सम संख्या का इकाई अंक और एक संख्या जिसका इकाई अंक 5 है उपस्थित होता है, वे हमेशा इकाई अंक में 0 देंगे, चाहे कोई अन्य संख्या उपस्थित हो या न हो।
उदाहरण 4. पहले 100 प्राकृतिक संख्याओं के उत्पाद के अंत में शून्य की संख्या क्या होगी?
उत्तर:

उदाहरण 5. 2347$98 में $ को कौन सा अक्षर प्रतिस्थापित करना चाहिए, ताकि यह 9 का गुणांक बन जाए?
उत्तर:
- जैसा कि आप जानते हैं कि यदि सभी अंकों का योग 9 से विभाज्य है, तो संख्या 9 से विभाज्य होती है।
- अब दिए गए अंकों का योग है: 2 + 3 + 4 + 7 + 9 + 8 = 33 + $। अब 33 के बाद के 9 के गुणांक यानी 36 के बारे में सोचें। इसका मतलब है कि आपको इसमें 3 जोड़ना है। $ का मान 3 है।
उदाहरण 6. एक पार्टी में, 20 लोग उपस्थित हैं। यदि उनमें से प्रत्येक अन्य व्यक्तियों के साथ हाथ मिलाता है, तो कुल कितने हाथ मिलेंगे?
उत्तर:
- 20 व्यक्तियों में से, पहला व्यक्ति 19 व्यक्तियों के साथ हाथ मिलाएगा।
- दूसरा व्यक्ति 18 व्यक्तियों के साथ हाथ मिलाएगा (क्योंकि उसने पहले व्यक्ति के साथ पहले ही हाथ मिलाया है)।
- तीसरा व्यक्ति 17 व्यक्तियों के साथ हाथ मिलाएगा और इसी तरह।
- दूसरा अंतिम व्यक्ति केवल एक व्यक्ति के साथ हाथ मिलाएगा।
- और अंतिम व्यक्ति किसी के साथ हाथ नहीं मिलाएगा (क्योंकि उसने पहले ही सभी व्यक्तियों के साथ हाथ मिला लिया है)।
- कुल हाथ मिलाने की संख्या ज्ञात करने के लिए, आपको 1 से 19 तक सभी स्वाभाविक संख्याओं को जोड़ना होगा, यानी ∑ 19। ∑19 = 19 x 20/2 = 190 हाथ मिलाने।
उदाहरण 7. 2354789341 को 11 से विभाजित करने पर शेषफल क्या है?
उत्तर:
- अजीब स्थान के अंकों का योग (O) = 1 + 3 + 8 + 4 + 3 = 19।
- सम स्थान के अंकों का योग (E) = 4 + 9 + 7 + 5 + 2 = 27।
- अंतर (D) = 19 - 27 = - 8
- शेषफल = 11 - 8 = 3।
टिप: जब किसी संख्या के अजीब संख्या के अंकों को उसके उल्टे के साथ जोड़ा जाता है, तो योग हमेशा 11 से विभाज्य होता है। उदाहरण: 2341 + 1432 = 3773, जो 11 से विभाज्य है।
⇒ कोई भी संख्या जो 6 बार लगातार लिखी गई है, 7 और 13 से विभाज्य होगी।
उदाहरण 8. यदि 567P55Q 88 से विभाज्य है; तो P + Q का मान ज्ञात करें।
(a) 11
(b) 12
(c) 5
(d) 6
(e) 10
उत्तर: सही उत्तर विकल्प (e) है।
- संख्या 8 से विभाज्य है, इसका मतलब है; अंतिम 3 अंकों द्वारा बनी संख्या 8 से विभाज्य होनी चाहिए, जो 55 Q हैं। केवल Q = 2 इस शर्त को पूरा करता है।
- 11 के विभाजन के नियम से, (2 + 5 + 7 + 5) - (5 + P + 6) 11 से विभाज्य है। इसलिए 8-P 11 से विभाज्य है।
- यदि P= 8, तो ही यह संभव है। इसलिए P = 8 और Q = 2।
- इसलिए, P + Q = 10।
उदाहरण 9. यदि पहले 100 प्राकृतिक संख्याएँ एक साथ लिखी जाती हैं ताकि एक बड़ा संख्या बने और इसे 8 से विभाजित किया जाए। तो शेषफल क्या होगा?
(a) 1
(b) 2
(c) 4
(d) 7
(e) ज्ञात नहीं किया जा सकता
उत्तर: सही उत्तर विकल्प (c) है।
- संख्या है 1234…..9899100।
- 8 के विभाजन के नियम के अनुसार, हम केवल अंतिम 3 अंकों की जांच करेंगे।
- यदि 100 को 8 से विभाजित किया जाए, तो शेषफल 4 होगा।
उदाहरण 10. जब 4444……..44 बार को 7 से विभाजित किया जाएगा, तो शेषफल क्या होगा? (क) 1 (ख) 2 (ग) 5 (घ) 6 (ङ) 0
उत्तर: सही उत्तर विकल्प (ख) है
- यदि 4 को 7 से विभाजित किया जाए, तो शेषफल 4 है।
- यदि 44 को 7 से विभाजित किया जाए, तो शेषफल 2 है।
- यदि 444 को 7 से विभाजित किया जाए, तो शेषफल 3 है।
- इस तरह जांचने पर, हम जान पाते हैं कि 444444 को 7 से ठीक से विभाजित किया जा सकता है।
- तो यदि हम छह 4 लेते हैं, तो यह 7 से ठीक से विभाजित होगा।
- इसी तरह, बारह 4 भी 7 से ठीक से विभाजित होंगे और 42 4 भी 7 से ठीक से विभाजित होंगे। तो 44 में से बचने वाले दो 4, शेषफल 2 देंगे।
सह-प्राइम या सापेक्ष प्राइम संख्याएँ
दो या अधिक संख्याएँ जो कोई सामान्य गुणांक साझा नहीं करतीं, उन्हें सह-प्राइम या सापेक्ष प्राइम कहा जाता है। दूसरे शब्दों में, उनका सबसे बड़ा सामान्य गुणांक 1 है।
यदि दो संख्याएँ m और n सापेक्ष प्राइम हैं, और एक प्राकृतिक संख्या x दोनों m और n द्वारा व्यक्तिगत रूप से विभाज्य है, तो x भी mn द्वारा विभाज्य है।
मुख्य अवधारणा 1: दो संख्याओं को सह-प्राइम के रूप में पहचानना महत्वपूर्ण है जब वे भिन्नों के हर में दिखाई देती हैं।
- यह अवधारणा एकउदाहरणसे सबसे अच्छे तरीके से समझाई जाती है: मान लीजिए M/8 + N/9, जहाँ M 8 द्वारा विभाज्य नहीं है और N 9 द्वारा विभाज्य नहीं है। ये संख्याएँ सह-प्राइम हैं, जिसका अर्थ है कि उनके पास 1 के अतिरिक्त कोई सामान्य गुणांक नहीं है। जब दो संख्याएँ सह-प्राइम होती हैं, तो परिणाम एक दशमलव भिन्न होता है, न कि एक पूर्णांक। इसका कारण यह है कि 8 और 9 सह-प्राइम हैं, और सह-प्राइम संख्याओं द्वारा विभाजित करने पर दशमलव परिणाम एक-दूसरे से मेल नहीं खाते।
- यह अवधारणा समस्याओं को हल करते समय विशेष रूप से महत्वपूर्ण होती है, खासकर शब्द समस्याओं में रैखिक समीकरणों से संबंधित मामलों में।
उदाहरण: 25x7y के रूप में सभी चार अंकों की संख्याएँ खोजें जो 36 द्वारा विभाज्य हैं।
उत्तर: चूँकि 36 दो सह-प्राइम संख्याओं, 4 और 9 का गुणनफल है, संख्या 25x7y को 36 द्वारा विभाजित होने के लिए 4 और 9 दोनों द्वारा विभाज्य होना चाहिए।
4 द्वारा विभाज्यता: 4 द्वारा विभाज्यता के लिए, संख्या के अंतिम दो अंक (7y) 4 द्वारा विभाज्य होने चाहिए। 7y को 4 द्वारा विभाज्य बनाने के लिए संभव मान y के लिए 2 और 6 हैं। इसलिए, y 2 या 6 हो सकता है।
9 द्वारा विभाज्यता: 9 द्वारा विभाज्यता के लिए, संख्या के अंकों का योग 9 द्वारा विभाज्य होना चाहिए। अंकों का योग है
यदि y = 2 है, तो योग है 2+5+x+7+2=16 + x. इसके 9 द्वारा विभाज्य होने के लिए, 16 + x का 9 का गुणज होना चाहिए। x का संभव मान 2 है (क्योंकि 16 + 2 = 18, जो 9 द्वारा विभाज्य है)। यदि y=6 है, तो योग है 2+5+x+7+6=20 + x. इसके 9 द्वारा विभाज्य होने के लिए, 20 + x का 9 का गुणज होना चाहिए। x के लिए संभव मान 7 है (क्योंकि 27 9 द्वारा विभाज्य है)।
इस प्रकार, संख्याएँ 25272 और 25776 36 द्वारा विभाज्य हैं।
मुख्य अवधारणा 2: दो संख्याओं को सह-प्राइम निर्धारित करने का एक अन्य तरीका उनके प्राथमिक गुणकों की जांच करना है। दो या अधिक संख्याएँ सह-प्राइम होने के लिए, उनके प्राथमिक गुणकों में कोई सामान्य तत्व नहीं होना चाहिए।
उदाहरण के लिए, यदि A और B सह-प्राइम हैं, और A = 2nx 3m है, तो B के प्राथमिक गुणकों में 2 या 3 शामिल नहीं होने चाहिए। इसके बजाय, यह अन्य प्राथमिक संख्याओं जैसे 5, 7, 11, आदि से बना होना चाहिए, लेकिन इसमें 2 या 3 गुणक के रूप में नहीं हो सकते।
हमेशा ध्यान में रखें
- संख्या 1 न तो प्रमुख है और न ही समुच्चय।
- 2 एकमात्र सम संख्या है जो प्रमुख है।
- (xn + yn) (x + y) से विभाज्य है, जब n विषम संख्या हो।
- (xn - yn) (x + y) से विभाज्य है, जब n सम संख्या हो।
- (xn - yn) (x - y) से विभाज्य है, जब n विषम या सम संख्या हो।
- 5 लगातार पूर्ण संख्याओं का योग हमेशा 5 से विभाज्य होगा।
- 2 संख्याओं के बीच का अंतर (xy) - (yx) हमेशा 9 से विभाज्य होगा।
- एक विषम संख्या का वर्ग जब 8 से विभाजित किया जाता है, तो हमेशा 1 शेषफल देता है।
- हर वर्ग संख्या 3 का गुणांक है या 3 के गुणांक से एक अधिक है।
- हर वर्ग संख्या 4 का गुणांक है या 4 के गुणांक से एक अधिक है।
- यदि एक वर्ग संख्या 9 पर समाप्त होती है, तो पूर्ववर्ती अंक सम है।
- यदि m और n दो पूर्णांक हैं, तो (m + n)! m! n! से विभाज्य है।
- (a)n / (a + 1) शेषफल छोड़ता है
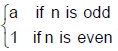
- n लगातार संख्याओं का गुणनफल हमेशा n! से विभाज्य होता है।
उदाहरण 1. यदि ‘X’ एक सम संख्या है; Y एक विषम संख्या है, तो निम्नलिखित में से कौन सी सम है?
(a) X2 + Y
(b) X + Y2
(c) X2 + Y2
(d) X2Y2
(e) इनमें से कोई नहीं
उत्तर: सही उत्तर विकल्प (d) है
- चूंकि X सम है, X2 सम है।
- Y विषम है, Y2 विषम है।
- इसलिए विकल्प (1), (2), (3) सम + विषम = विषम।
- विकल्प (4) है (सम) (विषम) = सम।
उदाहरण 2. 0.343434....… और 0.2343434…… के बीच का अंतर भिन्न रूप में क्या है?
(a) 6/55
(b) 6/11
(c) 9/55
(d) 9/13
(e) 5/11
उत्तर: सही उत्तर विकल्प (a)
0.343434.....= 34/99 और 0.23434.... = 234 - 2/990 = 232/990
∴ अंतर = 34/99 - 232/990 = 108/990 = 6/55
उदाहरण 3. निम्नलिखित संख्याओं में से कितनी कम से कम 3 विभिन्न प्रमुख संख्याओं द्वारा विभाज्य हैं: 231, 750, 288 और 1372?
(a) 0
(b) 1
(c) 2
(d) 3
(e) 4
उत्तर: सही उत्तर विकल्प (सी) है
- 231 = 3 × 7 × 11 (3 प्रमुख कारक)
- 750 = 2 × 3 × 53 (3 प्रमुख कारक)
- 288 = 25 × 32 (केवल 2 प्रमुख कारक)
- 1372 = 22 × 73 (केवल 2 प्रमुख कारक)
इसलिए, केवल 231 और 750 में 3 प्रमुख कारक हैं।
उदाहरण 4. n3 + 6n2 + 11n + 6 (जहां n एक पूर्ण संख्या है) हमेशा किससे विभाज्य है?
(a) 4
(b) 5
(c) 6
(d) 8
(e) 12
उत्तर: सही उत्तर विकल्प (सी) है
- n3 + 6n2 + 11n + 6 = (n + 1) (n + 2) (n + 3)।
- 3 लगातार संख्याओं का गुणनफल हमेशा 3! = 6 से विभाज्य होता है। (या) n = 0, 1, 2, 3 लेकर जांचें कि यह हमेशा 6 से विभाज्य है।
उदाहरण 5. यदि 351 × 352 × 353 × - - - - - - - × 356 को 360 से विभाजित किया जाए, तो शेषफल क्या होगा?
(a) 0
(b) 1
(c) 2
(d) 3
(e) 359
उत्तर: सही उत्तर विकल्प (ए) है
- चूंकि दिए गए 6 लगातार संख्याओं का गुणनफल है, यह हमेशा 6! = 720 से विभाज्य होता है।
- यह 360 से भी विभाज्य है। इसलिए, शेषफल 0 होगा।
एचसीएफ और एलसीएम के सिद्धांत
सर्वाधिक सामान्य गुणांक (HCF)
- सामान्य गुणांक: यदि दो संख्याएँ A और B किसी संख्या X द्वारा पूर्णतः विभाजित होती हैं, तो X A और B का एक सामान्य गुणांक या विभाजक है।
- सर्वाधिक सामान्य गुणांक: यह दो या अधिक संख्याओं का सबसे बड़ा गुणांक है। इसे GCF या GCD (सर्वाधिक सामान्य गुणांक या सर्वाधिक सामान्य विभाजक) भी कहा जाता है। उदाहरण के लिए, 4 और 8 का HCF = 4, 125 और 200 का HCF = 25।
- दिए गए संख्याओं का HCF निकालने के लिए:
1. दिए गए संख्याओं को उनके प्राइम फैक्टर में तोड़ें।
2. HCF सभी संख्याओं में सामान्य प्राइम फैक्टर का गुणनफल होगा।
आइए कुछ हल किए गए उदाहरणों की मदद से HCF निकालने की प्रक्रिया सीखते हैं।
प्रश्न: 96, 36 और 18 का HCF निकालिए।
उत्तर: सबसे पहले प्रत्येक संख्या को उनके प्राइम फैक्टर में तोड़ते हैं।
96 = 2 x 3 x 2 x 2 x 2 x 2,
36 = 2 x 3 x 2 x 3,
18 = 2 x 3 x 3।
इन संख्याओं के सभी सामान्य गुणांक लें और उन्हें गुणा करें।
इसलिए, 96, 36 और 18 का HCF उन संख्याओं में सामान्य गुणांकों की सबसे बड़ी संख्या का गुणनफल है, अर्थात् 2 x 3 = 6। दूसरे शब्दों में, 6 सबसे बड़ा पूर्णांक है, जो 96, 36 और 18 को बिना किसी शेष के विभाजित कर सकता है।
प्रश्न: 42 और 70 का HCF निकालिए।
उत्तर: 42 = 3 x 2 x 7,
70 = 5 x 2 x 7।
इसलिए, HCF = 7 = 14।
प्रश्न: 144, 630 और 756 का HCF निकालिए।
उत्तर: 144 = 24 x 32,
630 = 2 x 32 x 5 x 7,
756 = 22 x 33 x 7।
इसलिए, 144, 630, और 756 का HCF = 2 x 32 = 18.
महत्वपूर्ण:
- दो प्राइम संख्याओं का HCF हमेशा 1 होता है।
- को-प्राइम संख्याओं का HCF हमेशा 1 होता है।
एचसीएफ खोजने की शॉर्टकट विधि
चलो उदाहरणों का उपयोग करके संख्याओं के सेट का एचसीएफ (अधिकतम सामान्य भाजक) खोजने का एक तेज़ तरीका सीखते हैं।
उदाहरण 1: 39, 78, और 195 का एचसीएफ खोजें।
उत्तर: चरण-दर-चरण विधि पर ध्यान दें:
संख्याओं के बीच के अंतर पर ध्यान दें।
- किसी भी दो संख्याओं के बीच का अंतर लें। एचसीएफ को इन अंतरों का भाजक होना चाहिए।
- अंतर हैं:
- 78 − 39 = 39
- 195 − 39 = 156
- 195 − 78 = 117
- तो, एचसीएफ को 39, 156, और 117 को विभाजित करना चाहिए।
छोटे अंतर (39) से शुरू करें।
- एचसीएफ को 39 का भाजक होना चाहिए। 39 के भाजक हैं:
- 1, 3, 13, और 39।
- एचसीएफ को 39 का भाजक होना चाहिए। 39 के भाजक हैं:
सबसे बड़े भाजक (39) को सभी संख्याओं में विभाजित करें।
- क्या 39, 78 को विभाजित करता है? हाँ।
- क्या 39, 195 को विभाजित करता है? हाँ।
- तो, 39, 78, और 195 का एचसीएफ 39 है।
उदाहरण 2: 39, 78, और 182 का HCF ज्ञात करें।
उत्तर:
- संख्याओं के बीच का अंतर ज्ञात करें।
- 78−39=39
- 182−39=143
- 182−78=104
- 39 के गुणांक जांचें (1, 3, 13, 39)।
- क्या 39, 182 को विभाजित करता है? नहीं।
- क्या 39, 182 को विभाजित करता है? नहीं।
- अगले सबसे बड़े गुणांक, 13 को आजमाएं।
- क्या 13, 39 को विभाजित करता है? हाँ।
- क्या 13, 182 को विभाजित करता है? हाँ।
इसलिए, 39, 78, और 182 का HCF 13 है।
यह प्रक्रिया क्यों काम करती है?
- जब हम दो संख्याओं के बीच का अंतर ज्ञात करते हैं, तो उन संख्याओं का HCF उस अंतर का गुणांक होना चाहिए। इसका कारण यह है कि केवल वही संख्याएँ जो दोनों संख्याओं को विभाजित करती हैं, उनके अंतर को भी विभाजित करेंगी।
- छोटे अंतर से शुरू करके और इसके गुणांकों की जांच करके, हम बिना हर संख्या के लिए लंबी विभाजन विधि का उपयोग किए HCF को जल्दी से ज्ञात कर सकते हैं।
- यह विधि समय बचाती है और HCF को खोजना सरल बनाती है!
एलसीएम
किसी भी दो या अधिक संख्याओं का न्यूनतम समापवर्त्य (LCM) वह smallest संख्या है जो सभी द्वारा सही रूप से विभाजित होती है। दूसरे शब्दों में, यह दी गई संख्याओं के सभी प्रमुख गुणांकों की उच्चतम शक्तियों का गुणनफल है।
दी गई संख्याओं का LCM ज्ञात करने के लिए:
- दी गई संख्याओं को उनके प्रमुख गुणांकों में विभाजित करें।
- LCM सभी गुणांकों की उच्चतम शक्ति का गुणनफल होगा जो दी गई संख्याओं में मौजूद हैं।
आइए कुछ हल किए गए उदाहरण लेते हैं।
प्रश्न: 96, 36 और 18 का LCM ज्ञात करें।
उत्तर: पहले, प्रत्येक संख्या को उनके प्रमुख गुणांकों में विभाजित करें:
96 = 2 x 2 x 2 x 2 x 2 x 3 = 25 x 31,
36 = 2 x 2 x 3 x 3 = 22 x 32,
18 = 2 x 3 x 3 = 21 x 32
इसलिए, 96, 36 और 18 का LCM सभी प्रमुख गुणांकों की उच्चतम शक्तियों का गुणनफल है, अर्थात् 25 x 32 = 32 x 9 = 288।
अर्थात्, 288 वह smallest पूर्णांक है, जो 96, 36 और 18 द्वारा बिना कोई शेष छोड़ते विभाजित होता है।
प्रश्न: 42 और 70 का LCM ज्ञात करें।
उत्तर: 42 = 3 x 2 x 7,
70 = 5 x 2 x 7।
इसलिए, LCM = 2 x 3 x 5 x 7 = 210।
प्रमुख गुणांकरण की विधि के अलावा, दी गई संख्याओं का LCM ज्ञात करने के लिए एक और विधि है जिसे लंबी विभाजन विधि कहा जाता है। यह विधि तीन या अधिक संख्याओं के लिए LCM जल्दी प्राप्त करने में काफी सहायक है।
भाग विधि द्वारा LCM
संख्याएँ लिखें, उन्हें कोमा से अलग करें। फिर उन्हें बढ़ते क्रम में अभाज्य गुणकों (जैसे, 2, 3, 5, 7, आदि) द्वारा एक-एक करके विभाजित करें। फिर, प्रत्येक विभाजन के बाद, 'विभाजक (अभाज्य संख्या)' द्वारा पूरी तरह से विभाजित होने वाली प्रत्येक संख्या का भाग नीचे लिखें। जो संख्याएँ विभाजित नहीं हुई हैं, उन्हें वैसे ही छोड़ दें। ऐसा तब तक करते रहें जब तक प्रत्येक कॉलम में भाग के रूप में अभाज्य गुणक न मिल जाएं। सभी अभाज्य गुणकों (विभाजक और भाग) का गुणनफल LCM होगा।
प्रश्न: 8, 12, 15 और 21 का LCM ज्ञात करें
उत्तर:

इसलिए, LCM है 2 x 2 x 2 x 3 x 5 x 7 = 840।
महत्वपूर्ण:
- A, B और C का HCF सबसे बड़ा विभाजक है जो A, B, और C को पूरी तरह से विभाजित कर सकता है।
- A, B और C का LCM सबसे छोटा भाज्य है जो A, B, और C द्वारा पूरी तरह से विभाज्य है।
दो संख्याओं और उनके HCF और LCM के बीच एक बहुत महत्वपूर्ण संबंध है, जो नीचे दिया गया है।
इस संबंध पर आधारित कई समस्याएँ विभिन्न प्रतियोगी परीक्षाओं में आई हैं।
उदाहरण: दो संख्याओं का LCM और HCF क्रमशः 2079 और 27 है। यदि एक संख्या 189 है, तो दूसरी संख्या ज्ञात करें।
उत्तर: दूसरी संख्या होगी = 
इसलिए, आवश्यक संख्या = 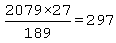
उदाहरण: दो संख्याएँ 3: 5 के अनुपात में हैं और उनका LCM 1500 है। संख्याओं का HCF ज्ञात करें।
उत्तर: मान लीजिए, दो संख्याएँ 3X और 5X हैं।
इसलिए, उनका HCF = X है, उपरोक्त दिए गए सूत्र का उपयोग करते हुए, हमें मिलता है LCM = 3 × 5 × X = 15X या, 15X = 1500 ⇒ X = 100.
इसलिए, संख्याओं का HCF 100 है।
भिन्नों का HCF और LCM
हम निम्नलिखित सीधे सूत्र का उपयोग कर सकते हैं।
भिन्नों का HCF = 
इसी प्रकार, भिन्नों का LCM = 
उदाहरण:दो भिन्नों 6/9, 12/15 का HCF और LCM ज्ञात करें।
उत्तर: अंश 6 और 12 हैं, उनका HCF = 6 और LCM = 12 है।
हर का 9 और 15 हैं, उनका LCM = 45 और HCF = 3 है।
इसलिए, आवश्यक HCF = 6/45 और LCM = 12/3 = 4।
उदाहरण: एक व्यक्ति 51 किमी और 85 किमी को एक निश्चित संख्या में मिनटों में चलाने की सबसे बड़ी संभव गति क्या है?
उत्तर: एक व्यक्ति की 51 किमी और 85 किमी को एक निश्चित संख्या में मिनटों में चलाने की सबसे बड़ी संभव गति ज्ञात करने के लिए, हमें 51 और 85 का सबसे बड़ा सामान्य कारक ज्ञात करना होगा। यह समस्या 51 किमी और 85 किमी की दूरी का HCF (Highest Common Factor) मांग रही है।
चरण-दर-चरण प्रक्रिया:
1. 51 और 85 का HCF ज्ञात करें:
- 51 के प्राथमिक गुणांक हैं: 51 = 3 × 17
- 85 के प्राथमिक गुणांक हैं: 85 = 5 × 17
51 और 85 के बीच सामान्य कारक 17 है।
2. परिणाम: एक व्यक्ति की एक निश्चित संख्या में मिनटों में चलाने की सबसे बड़ी संभव गति 17 किमी प्रति मिनट है, क्योंकि 17 वह सबसे बड़ा संख्या है जो 51 और 85 दोनों को ठीक से विभाजित करता है।
इसलिए, सबसे बड़ी संभव गति 17 किलोमीटर प्रति मिनट है।
शेषफल
- हम जानते हैं कि जब एक संख्या M को दूसरी संख्या N से विभाजित किया जाता है, और यदि M > N है, तो शेषफल की गणना M से N के अधिकतम संभव गुणांक को घटाकर की जाती है।
- इस प्रक्रिया में घटाने के बाद बची हुई अधिशेष राशि को शेषफल कहा जाता है, N का अधिकतम गुणांक उत्पादक कहा जाता है, और M और N को क्रमशः आय और भाजक कहा जाता है।
- इनके बीच निम्नलिखित संबंध है:
आय = उत्पादक x भाजक + शेषफल
शेषफल के बारे में महत्वपूर्ण बिंदु
- शेषफल हमेशा भाजक से कम होता है।
- यदि शेषफल 0 है, तो भाजक को आय का गुणनखंड कहा जाता है।
- यदि आय भाजक से कम है, तो शेषफल स्वयं आय है।
उदाहरण: 6 से 5 विभाजित करने पर शेषफल केवल 5 है।
- शेषफल हमेशा इसके वास्तविक रूप में ही गणना किया जाना चाहिए। अर्थात् इसे सबसे सरल रूप में नहीं घटाना चाहिए।
उदाहरण: जब 6 से 4 विभाजित किया जाता है, तो शेषफल 4 है और NOT 2।
शेष प्रमेय
शेष प्रमेय हमें बिना पूरे उत्पाद को गणना किए हुए यह जानने में मदद करता है कि एक संख्या द्वारा भाग देने पर शेषफल क्या होगा। आइए इसे 12 से विभाजित 17 x 23 के उदाहरण के साथ समझते हैं।
चरण-दर-चरण व्याख्या:
संख्याओं को फिर से लिखें: हम 17 और 23 को इस तरह व्यक्त कर सकते हैं कि वे 12 को शामिल करें:
17 = 12 + 5,
23 = 12 + 11।
इसलिए, हम अभिव्यक्ति को फिर से लिख सकते हैं:
17 x 23 = (12 + 5) x (12 + 11)अभिव्यक्ति का विस्तार करें: वितरणीय गुण का उपयोग करते हुए, अभिव्यक्ति का विस्तार करें:
(12+5)(12+11) = 12 x 12 + 12 x 11 + 5 x 12 + 5 x 11संख्याओं की पहचान करें:
12 x 12 (12 से विभाज्य है, इसलिए इसका शेषफल 0 है)
12 x 11 (12 से विभाज्य)
5 x 12 (12 से विभाज्य)
अंतिम पद: 5 x 11अंतिम पद पर ध्यान केंद्रित करें: 12 से विभाजित करते समय शेषफल पर प्रभाव डालने वाला एकमात्र पद 5 x 11 है।
5 x 11 = 55शेषफल ज्ञात करें: अब, हमें यह ज्ञात करना है कि 55 को 12 से भाग देने पर शेषफल क्या होगा:
55 / 12 = 4 और शेष 7
इस प्रकार, 17 x 23 को 12 से विभाजित करने पर शेषफल 7 है।
शेष प्रमेय शेषफल ज्ञात करने की प्रक्रिया को सरल बनाता है, क्योंकि यह केवल संबंधित पदों पर ध्यान केंद्रित करता है जब संख्याओं को भाजक के सापेक्ष फिर से लिखा जाता है। हमारे उदाहरण में, हमें केवल अंतिम पद 5×11 पर विचार करने की आवश्यकता थी ताकि शेषफल ज्ञात हो सके।
नकारात्मक शेष का अवधारणा
गणित में, शेष हमेशा गैर-ऋणात्मक पूर्णांक होता है। हालाँकि, हम ऋणात्मक पूर्णांक की अवधारणा का उपयोग कई प्रश्नों को आसानी से और कम गणना के साथ हल करने के लिए कर सकते हैं।
इसे समझने के लिए एक उदाहरण लेते हैं:
हमें पता है कि 15 को 4 से विभाजित करने पर प्राप्त शेष 3 है क्योंकि 15, 4 का निकटतम गुणांक, अर्थात् 12 से 3 अधिक है। यहाँ हम 15 की तुलना 12 से कर रहे हैं (जो 15 से कम या उसके बराबर 4 का सबसे बड़ा गुणांक है) और पाया कि 15, 12 से 3 अधिक है और इसलिए अधिकता 3 है, जो शेष है। यदि हम 12 की तुलना में 15 की तुलना 16 से करते हैं (जो 15 के निकट 4 का एक और गुणांक है), तो हम कह सकते हैं कि 15, 16 से 1 कम है। या 15 को 4 से विभाजित करने के लिए 1 की कमी है। इस कमी वाले संख्या को नकारात्मक शेष कहा जाता है। अर्थात्, हम कह सकते हैं कि जब 15 को 4 से विभाजित किया जाता है, तो शेष -1 है।
नकारात्मक शेष से संबंधित सकारात्मक शेष में परिवर्तन और इसके विपरीत
- यदि N को 5 से विभाजित करने पर प्राप्त शेष -2 है, तो सकारात्मक शेष 5-2 = 3 है। इसी प्रकार, यदि 7 से किसी संख्या को विभाजित करने पर प्राप्त सकारात्मक शेष 4 है, तो नकारात्मक शेष 4-7 = -3 होगा।
- हम इस अवधारणा का उपयोग कुछ उदाहरणों को हल करने में करेंगे ताकि नकारात्मक शेष के अनुप्रयोग को समझ सकें।
नोट: किसी भी दो या अधिक संख्याओं का गुणन, जोड़ और घटाव किसी भी प्राकृतिक संख्या द्वारा विभाजित करने पर वही शेष देता है, जैसे कि उनके शेषों का संबंधित गुणन, जोड़ और घटाव।
आइए इसे एक उदाहरण से समझते हैं:
एक संख्या N = लें।
(24 x 8 + 12 - 7)
अब N को 5 से विभाजित करने पर शेषफल ज्ञात करें।एक तरीका यह है कि हम सबसे पहले N = i.e का मान ज्ञात करें(24 x 8 + 12 - 7)
जो 197 के बराबर है। और फिर इस संख्या को 5 से विभाजित करने पर शेषफल = 2 प्राप्त करें।दूसरा तरीका यह है कि हम N में दी गई प्रत्येक संख्या को 5 से विभाजित करके उसके शेषफल की गणना करते हैं और फिर इन शेषफलों के साथ संगत गणितीय ऑपरेटरों का उपयोग करते हैं।
24 को 5 से विभाजित करने पर प्राप्त शेष = 4,
8 को 5 से विभाजित करने पर प्राप्त शेष = 3,
12 को 5 से विभाजित करने पर प्राप्त शेष = 2,
7 को 5 से विभाजित करने पर प्राप्त शेष = 2
संख्याओं को उनके संगत शेष से प्रतिस्थापित करने पर,(4 x 3 + 2 - 2) = 12
चूँकि 12, 5 से बड़ा है, इसलिए हमने 12 को पुनः 5 से विभाजित करके अंतिम शेष = 2 प्राप्त किया।
नोट: दिए गए उदाहरण के लिए दूसरा तरीका कठिन या निरर्थक लग सकता है। लेकिन विस्तृत स्पष्टीकरण समझने के उद्देश्य से दिए गए हैं, हम देखेंगे कि इस दूसरे तरीके को लागू करके हम कैसे उन्नत समस्याओं को हल कर सकते हैं।
दूसरे दृष्टिकोण के साथ उपरोक्त समस्या में सकारात्मक शेष और ऋणात्मक शेष की अवधारणा दोनों को एक साथ लागू करना:
24 को 5 से विभाजित करने पर प्राप्त शेष = -1
8 को 5 से विभाजित करने पर प्राप्त
शेष = -2 12 को 5 से विभाजित करने पर प्राप्त शेष = 2
7 को 5 से विभाजित करने पर प्राप्त शेष = 2
संख्याओं को उनके संगत शेष के साथ बदलने पर हमें प्राप्त होता है,
((-1) x (-2) + 2 - 2) = 1
परिचय: संख्या प्रणाली इसलिए अंतिम शेष = 2.
हल किये गए उदाहरण
प्रश्न: 123 × 124 × 125 को 9 से विभाजित करने पर शेष क्या है?उत्तर: जब 123 को 9 से विभाजित किया जाता है तो प्राप्त शेष = -3 है।
जब 124 को 9 से विभाजित किया जाता है तो प्राप्त शेष = -2 है।
जब 123 को 9 से विभाजित किया जाता है तो प्राप्त शेष = -1 है।
अंतिम शेष = (-3)(-2)(-1) = -6। आवश्यक सकारात्मक शेष = 9-6 = 3।
प्रश्न: 1! + 2! + 3! + …. + 100! को 5 से विभाजित करने पर शेष क्या है।
उत्तर: देखिए कि श्रृंखला में 5! से आगे हर संख्या 5 से विभाजित है, अर्थात् प्रत्येक मामले में शेष 0 है।
तो आवश्यक शेष केवल पहले 4 संख्याओं को विभाजित करके प्राप्त किया जाता है।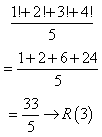
चक्रवातिता
1. अंक 0, 1, 5 और 6:
जब हम इन अंकों के व्यवहार का अवलोकन करते हैं, तो ये सभी किसी भी घात में उठाए जाने पर अपने स्वयं के अंक के समान इकाई अंक रखते हैं, अर्थात् 0n = 0, 1n = 1, 5n = 5, 6n = 6।
52 = 25: इकाई अंक 5 है, जो स्वयं संख्या है।
16 = 1: इकाई अंक 1 है, जो स्वयं संख्या है।
04 = 0: इकाई अंक 0 है, जो स्वयं संख्या है।
63 = 216: इकाई अंक 6 है, जो स्वयं संख्या है।
आइए इस अवधारणा को निम्नलिखित उदाहरण पर लागू करें।
उदाहरण: निम्नलिखित अंकों का इकाई अंक खोजें:
- 185563
उत्तर = 5 - 2716987
उत्तर = 1 - 15625369
उत्तर = 6 - 190654789321
उत्तर = 0
2. अंकों 4 और 9:
इन दोनों अंकों में केवल दो विभिन्न अंकों की चक्रता होती है, जो कि उनके एकक अंक के रूप में होती है।
- 42 = 16: इकाई अंक है 6।
- 43 = 64: इकाई अंक है 4।
- 44 = 256: इकाई अंक है 6।
- 45 = 1024: इकाई अंक है 4।
- 92 = 81: इकाई अंक है 1।
- 93 = 729: इकाई अंक है 9।
यह देखा जा सकता है कि एकक अंक 6 और 4 एक विषम-सम क्रम में दोहराए जा रहे हैं। अतः, 4 की चक्रता 2 है। 9 के लिए भी ऐसा ही है।
इसे निम्नलिखित रूप में सामान्यीकृत किया जा सकता है:
उदाहरण: निम्नलिखित संख्याओं का एकक अंक ज्ञात करें:
- 189562589743
उत्तर = 9 (क्योंकि घात विषम है) - 279698745832
उत्तर = 1 (क्योंकि घात सम है) - 154258741369
उत्तर = 4 (क्योंकि घात विषम है) - 19465478932
उत्तर = 6 (क्योंकि घात सम है)

3. अंक 2, 3, 7 और 8:
ये अंक 4 विभिन्न संख्याओं का पावर चक्र रखते हैं।
2 1 = 2 , 2 2 = 4 , 2 3 = 8 और 2 4 = 1 6 और उसके बाद यह दोहराना शुरू हो जाता है ।
तो, 2 की चक्रीयता में 4 अलग-अलग संख्याएँ 2, 4, 8, 6 हैं।
3 1 = 3 , 3 2 = 9 , 3 3 = 2 7 और 3 4 = 8 1 और उसके बाद यह दोहराना शुरू हो जाता है।
तो, 3 की चक्रीयता में 4 अलग-अलग संख्याएँ 3, 9, 7, 1 हैं।
7 और 8 समान तर्क का पालन करते हैं।
इसलिए इन चार अंकों यानी 2, 3, 7 और 8 में चार चरणों की एक इकाई अंक चक्रीयता है।
चक्रता तालिका
उपरोक्त चर्चा किए गए विचारों का सारांश दिए गए तालिका में प्रस्तुत किया गया है।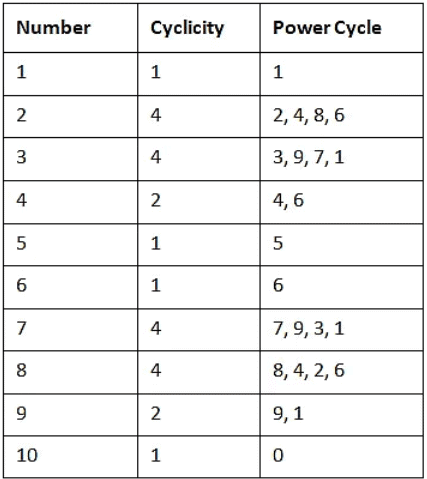
किसी संख्या की पावर की अवधारणा या चक्रता हमें बिना पूरे गणना किए एक बड़ी शक्ति में उठाई गई संख्या का अंतिम अंक जानने में मदद करती है। यह अंतिम अंक की संख्या पर निर्भर करते हुए दोहराने वाले पैटर्न पर आधारित है। एक तालिका हमें इस अंतिम अंक की भविष्यवाणी करने में मदद करती है। इसके अलावा, जो अंक एक या दो बार आते हैं, वे हर चार बार में दोहराए जाते हैं। इसलिए, प्रत्येक अंक हर चार बार में दोहराता है।
शून्य की संख्या
1. एक अभिव्यक्ति में शून्य की संख्या
चरण 1
- मान लीजिए कि आपको गुणन में शून्य की संख्या ज्ञात करनी है: 24 × 32 × 17 × 23 × 19।
- हम पहले इसे इसके प्रधान गुणांक के रूप में प्राप्त करते हैं, अर्थात् 23∗31∗25∗171∗19∗23।
- जैसा कि आप देख सकते हैं, इस उत्पाद में कोई शून्य नहीं होगा क्योंकि इसमें 5 का अभाव है।
- हालांकि, यदि आपके पास एक अभिव्यक्ति है जैसे 8 × 15 × 23 × 17 × 25 × 22।
- उपरोक्त अभिव्यक्ति को मानक रूप में फिर से लिखा जा सकता है: 23∗31∗51∗23∗17∗52∗21∗111
चरण 2
- शून्य 2 × 5 के संयोजन से बनते हैं।
- इसलिए, शून्य की संख्या उस 2’s और 5’s के जोड़ों की संख्या पर निर्भर करेगी जो बन सकते हैं।
- उपर्युक्त उत्पाद में चार 2 हैं और तीन 5 हैं। इसलिए, हम केवल तीन (2 × 5) के जोड़े बना सकेंगे।
- इसलिए, उत्पाद में 3 शून्य होंगे।
2. फैक्ट्रियल मान में शून्य की संख्या खोजना
- विधि 1: मान लीजिए कि आपको 6! में शून्य की संख्या खोजना है। 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1)।
5 की संख्या गिनने से उत्तर मिलेगा। - विधि 2: 6! में शून्य खोजने के लिए हम का उपयोग करते हैं।
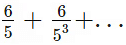
इसलिए हमें उत्तर 1 मिलता है क्योंकि श्रृंखला में पहले पद के बाद सभी विभाजन दशमलव में हैं जिन्हें हम नजरअंदाज करते हैं।
प्रश्न: 12 × 15 × 5 × 24 × 13 × 17
(क) 0
(ख) 1
(ग) 2
(घ) 3
उत्तर: (ग)
हल: 2 2 ∗3∗3∗5∗5∗2 3 ∗3∗13∗17 = इसलिए (5*2) के जोड़े 2 हैं, इसलिए हमारे पास 2 शून्य हैं।
3. एक विशेष अर्थ
- जब हम 45!, 46!, 47!, 48!, 49! का समाधान करते हैं, तो हर एक मामले में शून्यों की संख्या 10 के बराबर होगी।
- यह समझना मुश्किल नहीं है कि इन सभी फैक्टोरियल्स में फाइव की संख्या 10 के बराबर है। शून्यों की संख्या केवल 50! पर बदलेगी (यह 12 हो जाएगी)।
- वास्तव में, यह सभी फैक्टोरियल मानों के लिए सच होगा जो 5 के दो लगातार गुणन के बीच हैं।
- इस प्रकार, 50!, 51!, 52!, 53! और 54! में 12 शून्य होंगे (क्योंकि इनमें सभी में 12 फाइव हैं)। इसी तरह, 55!, 56!, 57!, 58! और 59! में प्रत्येक में 13 शून्य होंगे।
- जबकि 49! में 10 शून्य हैं, वहीं 50! में सीधे 12 शून्य हैं। इसका मतलब है कि कोई भी फैक्टोरियल मान ऐसा नहीं होगा जो 11 शून्य दे। यह इसलिए होता है क्योंकि 50! प्राप्त करने के लिए हम 49! के मान को 50 से गुणा करते हैं। जब आप ऐसा करते हैं, तो उत्पाद में दो 5 का परिचय होता है। इसलिए, शून्यों की संख्या दो से बढ़ जाती है।
- नोट: 124! पर आपको 24 + 4 = 28 शून्य मिलेंगे। 125! पर आपको 25 + 5 + 1 = 31 शून्य मिलेंगे। (3 शून्यों की छलांग।)
उदाहरण: n! में 13 शून्य हैं। n के उच्चतम और न्यूनतम मान क्या हैं?
(क) 57 और 58
(ख) 59 और 55
(ग) 59 और 6
(घ) 79 और 55
उत्तर: (ख)
हल: 55 पर हमें 13 शून्य मिलते हैं, क्योंकि हमें पता है कि 50! में 12 शून्य हैं, इसलिए 54! तक हमें 12 शून्य मिलेंगे। तो 55 से 59! में 13 शून्य होंगे।
आधार प्रणालियाँ
1. दशमलव संख्या प्रणाली (आधार-10)
2. द्विआधारी संख्या प्रणाली (आधार-2)
3. ऑक्टल संख्या प्रणाली (आधार-8)
4. हेक्साडेसिमल संख्या प्रणाली (आधार-16)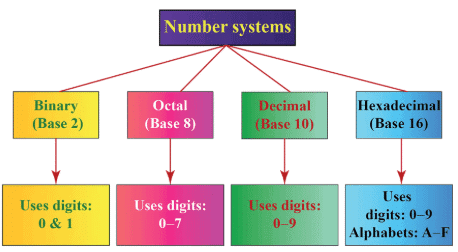
1. दशमलव संख्या प्रणाली (आधार-10)
दशमलव संख्या प्रणाली, जिसका आधार 10 है, में 0 से 9 तक अंक होते हैं। दशमलव बिंदु के बाईं ओर की स्थितियां 10 की शक्तियों को दर्शाती हैं, जो इकाइयों, दहाई, सैकड़ों आदि को इंगित करती हैं।
उदाहरण: 3567.89
इस उदाहरण में, अंक 3 हजार के स्थान पर है (10 3 ), अंक 5 सैकड़ों के स्थान पर है (10 2 ), अंक 6 दहाई के स्थान पर है (10 1 ), अंक 7 इकाइयों के स्थान पर है (10 0 या 1 ), अंक 8 दसवें स्थान पर है और अंक 9 सौवें स्थान पर है।
2. द्विआधारी संख्या प्रणाली (आधार-2)
बाइनरी या आधार-2 में केवल दो अंक होते हैं, 0 और 1. बाइनरी संख्याएँ, जैसे 110101, इन दो अंकों के संयोजन से बनी होती हैं.
उदाहरण: 110101
सबसे दायाँ अंक 2 0 है , अगला 2 1 है , फिर 2 2 है , और इसी तरह आगे भी. बाइनरी संख्या 110101 दशमलव प्रणाली में (1 * 2 5 ) + (1 * 2 4 ) + (0 * 2 3 ) + (1 * 2 2 ) + (0 * 2 1 ) + (1 * 2 0 ) = 53 के बराबर है.
3. ऑक्टल संख्या प्रणाली (आधार-8)
8 के आधार और 0 से 7 अंकों वाले ऑक्टल का उपयोग कंप्यूटिंग में किया जाता है। ऑक्टल को दशमलव में बदलने की प्रक्रिया मानक दशमलव रूपांतरण के समान ही है।
उदाहरण: 745
उदाहरण 745 में, सबसे दायाँ अंक 8 0 है , अगला 8 1 है , और सबसे बायाँ अंक 8 2 है । इसे दशमलव में बदलने पर, दशमलव प्रणाली में ऑक्टल संख्या 745 (7 * 8 2 ) + (4 * 8 1 ) + (5 * 8 0 ) = 485 के बराबर है।
4. हेक्साडेसिमल संख्या प्रणाली (आधार-16)
हेक्साडेसिमल में आधार 16 का उपयोग किया जाता है और यह 0 से 9 तक की संख्याओं को दर्शाता है, फिर 10 से 15 तक के मानों के लिए A से F का उपयोग करता है। यह एक ऐसी प्रणाली है जिसका उपयोग आम तौर पर कंप्यूटिंग में किया जाता है।
उदाहरण: 1A3F
उदाहरण 1A3F में, यह दशमलव प्रणाली में (1 * 16 3 ) + (10 * 16 2 ) + (3 * 16 1 ) + (15 * 16 0 ) = 6719 के बराबर है।
प्रश्न 1: 55552345 + 66665678 का अंतिम अंक खोजें
(क) 1
(ख) 3
(ग) 5
(घ) 7
उत्तर: (क)
चूंकि अंतिम अंक केवल अंतिम अंकों पर निर्भर करता है, इसलिए केवल अंतिम अंकों की घातों पर विचार करें, अर्थात 5 2345 + 6 5678।
जैसा कि हम जानते हैं, 5 की कोई भी घात केवल 5 पर समाप्त होती है और 6 की कोई भी घात केवल 6 पर समाप्त होती है।
52345 + 65678 का अंतिम अंक = 5 + 6 = 11 = 1
इसलिए, विकल्प (A) सही उत्तर है।
प्रश्न 2: यदि एक दो अंकों की संख्या में, इकाई स्थान पर अंक z है और दस स्थान पर अंक 8 है, तो संख्या है
(क) 80z + z
(ख) 80 + z
(ग) 8z + 8
(घ) 80z + 1
उत्तर: (ख)
इकाई स्थान पर अंक = z
दस स्थान पर अंक = 8
= 2-अंकीय संख्या = (10×8) + (1×z)
= 80 + z
प्रश्न 3: 60! में कितने अंतिम शून्य (संख्या के अंत में शून्य) हैं?
(क) 14
(ख) 12
(ग) 10
(घ) 8
उत्तर: (क)
- सबसे पहले, किसी संख्या के दशमलव निरूपण में अंतिम शून्यों की संख्या = 10 की उच्चतम घात जो संख्या को विभाजित कर सकती है।
उदाहरण के लिए,
3600 = 36 * 102
45000 = 45 * 103- इस प्रश्न का उत्तर देने के लिए, आइए सबसे पहले वह सबसे छोटा फैक्टोरियल देखें जो शून्य पर समाप्त होता है।
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
अब, 5! शून्य पर समाप्त होता है क्योंकि 1 * 2 * 3 * 4 * 5 की गणना करने पर हमें 10 का गुणनफल प्राप्त होता है।
10 = 2 * 5, इसलिए जब भी फैक्टोरियल में 2 और 5 आता है, हमें 10 का एक फैक्टर मिलता है।
तो, 5! में 1 शून्य है। 2 शून्य पर समाप्त होने वाला फैक्टोरियल 10 है!
15! में 3 शून्य हैं।
20! में 4 शून्य हैं और इसी तरह आगे भी।
2 और 5 के मिलने पर हर बार एक अतिरिक्त शून्य बनता है। प्रत्येक सम संख्या दो देती है, जबकि प्रत्येक पांचवीं संख्या हमें 5 देती है।- अब, यहाँ महत्वपूर्ण बात यह है कि चूँकि प्रत्येक सम संख्या फैक्टोरियल में कम से कम 2 का योगदान करती है, इसलिए 2 5 की तुलना में अधिक बार आता है। इसलिए, 10 की वह उच्चतम शक्ति ज्ञात करने के लिए जो किसी संख्या को विभाजित कर सकती है, हमें 5 की वह उच्चतम शक्ति गिननी होगी जो उस संख्या को विभाजित कर सकती है। हमें सिस्टम में 2 की संख्या गिनने की आवश्यकता नहीं है क्योंकि किसी भी फैक्टोरियल में 5 की तुलना में 2 अधिक होंगे।
- अब, 5 का हर गुणक फैक्टोरियल में एक शून्य जोड़ेगा। 1 * 2 * 3 *.......59 * 60 में 5 के बारह गुणक हैं। तो, ऐसा लगता है कि 60! 12 शून्यों पर समाप्त होगा। लेकिन हमें यहाँ एक और समायोजन करने की आवश्यकता है।
- 25 = 5 2 , इसलिए 25 अकेले दो 5 का योगदान देगा, और इसलिए सिस्टम में दो शून्य जोड़ देगा। इसी तरह, 25 का कोई भी गुणक एक अतिरिक्त शून्य का योगदान देगा।
- तो, 20! में 4 शून्य हैं, 25! में 6 शून्य हैं।
60! में [60/5] शून्य होंगे जो के गुणकों के कारण उत्पन्न होंगे और 25 और 50 की उपस्थिति के कारण एक अतिरिक्त [60/25] होगा।
{हम [60/25] के केवल पूर्णांक घटक को बनाए रखते हैं क्योंकि दशमलव भाग का कोई मान नहीं है}- अतः 60! का अंत 12 + 2 शून्य = 14 शून्य पर होगा।
- सामान्यतः, कोई भी n!
शून्य पर समाप्त होगा।
- आगे सामान्यीकरण करते हुए, यदि हम 3 की उच्चतम घात ज्ञात करना चाहते हैं जो n! को विभाजित करती है, तो यह कुछ और नहीं बल्कि है
- 7 की वह उच्चतम घात जो n! को विभाजित करती है, है
- किसी भाज्य संख्या के मामले में, हमें उसके अवयवी अभाज्य संख्याओं को तोड़ना होगा तथा संख्या को विभाजित करने वाली उच्चतम घात की गणना करनी होगी।
- उदाहरण के लिए, यदि हम 15 की सबसे बड़ी शक्ति ज्ञात करना चाहते हैं जो n! को विभाजित करती है, तो यह 3 और 5 की उच्चतम शक्तियों द्वारा संचालित होगी जो n! को विभाजित करती हैं। पिछले शून्यों के साथ हमने जो परिदृश्य देखा, उसके समान, हम देख सकते हैं कि किसी भी फैक्टोरियल में 5 की तुलना में कम से कम 3 अवश्य होंगे। इसलिए, 15 की उच्चतम शक्ति जो n! को विभाजित करती है, वह बस [n/5] + [n/25] + [n/125] + [n/625] है............
- अतः उत्तर "14" है

प्रश्न 4: गुणनफल के अंत में शून्यों की संख्या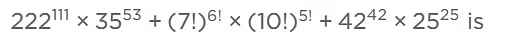
(ए) 42
(बी) 53
(सी) 1055
(डी) इनमें से कोई नहीं
उत्तर: (ए)
222 111 × 35 53 के अंत में शून्यों की संख्या 53 है
। (7!) 6! ×(10!) 5! के अंत में शून्यों की संख्या 960 है । 42 42 ×25 25 के
अंत में शून्यों की संख्या 42 है । इस प्रकार पूरे व्यंजक के अंत में शून्यों की संख्या 42 है।
प्रश्न 5. 100 ≤ n ≤ 200 में कितने सम पूर्णांक n हैं, जो न तो सात से और न ही नौ से विभाज्य हैं
(ए) 40
(बी) 37
(सी) 39
(डी) 38
उत्तर: (सी)
100 और 200 के बीच, दोनों शामिल हैं, कुल 51 सम संख्या हैं। इनमें से 7 सम संख्या हैं जो 7 से विभाज्य हैं और 6 संख्या जो 9 से विभाज्य हैं तथा 1 संख्या जो दोनों से विभाज्य है। इसलिए कुल मिलाकर 51 - (7+6-1) = 39। एक और विधि है जिसके माध्यम से हम उत्तर प्राप्त कर सकते हैं। चूंकि हमें सम संख्याएँ खोजनी हैं, इसलिए 100 और 200 के बीच 14, 18 और 126 से विभाजित संख्याओं पर विचार करें। ये क्रमशः 7, 6 और 1 हैं।
प्रश्न 6. सकारात्मक पूर्णांक (a, b) की कितनी जोड़ी हैं, ऐसी कि a ≤ b और ab = 42017?
(ए) 2018
(बी) 2019
(सी) 2017
(डी) 2020
उत्तर: (सी)
ab = 4 2017 = 2 4034
कुल कारकों की संख्या = 4035.
इन 4035 कारकों में से, हम दो संख्याएँ a, b चुन सकते हैं जैसे कि a < b in [4035/2] = 2017.
और चूँकि दी गई संख्या एक पूर्ण वर्ग है, इसलिए हमारे पास बराबर कारकों का एक समूह है।
∴ कई सकारात्मक पूर्णांकों के जोड़े (a, b) ऐसे हैं जैसे कि a ≤ b और ab = 4 2017 = 2018.
|
142 videos|172 docs|185 tests
|
FAQs on परिचय: संख्या प्रणाली - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
| 1. सर्वाधिक सामान्य गुणांक (HCF) और न्यूनतम सामान्य गुणांक (LCM) क्या होते हैं? |  |
| 2. HCF और LCM को कैसे निकाला जाता है? |  |
| 3. HCF और LCM का एक दूसरे से क्या संबंध है? |  |
| 4. HCF और LCM का उपयोग कहाँ होता है? |  |
| 5. HCF और LCM की गणना में आम गलतियाँ क्या हैं? |  |