Best Study Material for Bank Exams Exam
Bank Exams Exam > Bank Exams Notes > Quantitative Aptitude/संख्यात्मक योग्यता > संख्यात्मक प्रणाली: शेषफल खोजना
संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams PDF Download
GMAT में, शेष समस्याओं में यह समझना शामिल है कि जब एक संख्या को दूसरी संख्या से विभाजित किया जाता है तो शेष राशि कैसे ज्ञात की जाती है।
ये समस्याएँ संख्या गुणों, विभाज्यता नियमों और कुशल गणना विधियों की आपकी समझ का परीक्षण करती हैं।
जब किसी संख्या A को किसी संख्या B से विभाजित किया जाता है, तो इसे इस रूप में दर्शाया जा सकता है: A = B × Q + R
कहाँ,
- A लाभांश है ,
- B भाजक है
- Q भागफल (विभाजन का परिणाम) है , और
- R शेष है , जो संतुष्ट करना चाहिए 0 ≤ आर< बी.
शेष क्या है?
- जब आप एक संख्या, जिसे " लाभांश " कहते हैं, को दूसरी संख्या, जिसे " भाजक " कहते हैं, से विभाजित करते हैं, तो परिणाम को भिन्न के रूप में व्यक्त किया जाता है, जैसे "लाभांश/भाजक।"
- एक सरल उदाहरण में, जैसे 6 को 3 से भाग देना (6/3), उत्तर 2 है, जो कि " भागफल " है।
- हालांकि, सभी विभाजन समस्याएं 6/3 की तरह सीधी नहीं होतीं; कुछ का परिणाम " शेष" होता है, जो मूलतः तब होता है जब एक संख्या दूसरी संख्या को पूरी तरह से विभाजित नहीं करती है, तथा पीछे एक संख्या छोड़ती है, जिसे शेष कहा जाता है।
- सरल शब्दों में कहें तो, शेष वह भिन्नात्मक भाग है जो दो संख्याओं को विभाजित करने पर बचता है, तथा विभाजन के फलस्वरूप पूर्ण संख्या भागफल प्राप्त नहीं होता है ।
- उदाहरण के लिए, जब आप 15 को 4 से विभाजित करते हैं, तो शेषफल 3 बचता है।
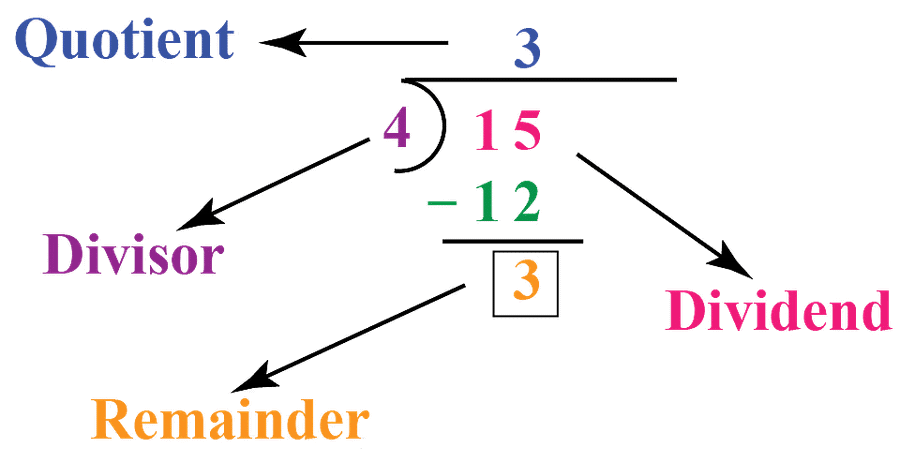
- शेष को मिश्रित संख्याओं के रूप में सोचना मददगार हो सकता है। उदाहरण के लिए, भिन्न 8/3 मिश्रित संख्या 2 के बराबर है 2/3.। यहाँ, 2/3 शेष को दर्शाता है, जो दर्शाता है कि पूर्ण संख्या बनाने के लिए आवश्यक 3 भागों में से 2 भाग बचे हैं। भिन्न का हर हमेशा भाजक के समान होगा।
गुणनफल का शेषफल ज्ञात करना (शेषफल व्युत्पन्न प्रमेय)
(i) यदि ' a1 ' को ' n ' से भाग दिया जाए तो शेष ' r1 ' प्राप्त होगा तथा यदि ' a2 ' को ' n ' से भाग दिया जाए तो शेष r2 प्राप्त होगा । तब,
(a) यदि a1 + a2 को n से विभाजित किया जाए, तो शेष r1 + r2 होगा ।
(b) यदि a1 - a2 को n से विभाजित किया जाए, तो शेष r1 - r2 होगा ।
(c) यदि a1 × a2 को n से विभाजित किया जाए, तो शेष r1 × r2 होगा ।
ऋणात्मक शेष की अवधारणा
- जब आप किसी ऋणात्मक संख्या को किसी धनात्मक संख्या से विभाजित करते हैं, तो कभी-कभी शेषफल ऋणात्मक हो सकता है।
- लेकिन हमें आमतौर पर शेष राशि को सकारात्मक और 0 और भाजक के बीच रखना होता है। इसलिए हम इसे सकारात्मक करने के लिए समायोजित करते हैं।
उदाहरण के लिए, -8 को 5 से भाग दें।
हल:
चरण 1: -8 को 5 से भाग दें: -8 ÷ 5 का भागफल -2 है, और शेष -3 है। इसे इस प्रकार लिखा जा सकता है:
-8 = 5 × (-2) + (-3)
चरण 2: शेष ऋणात्मक (-3) है। शेष को धनात्मक बनाने के लिए, 5 को -3 में जोड़ें:
-3 + 5 = 2
चरण 3: अब शेष धनात्मक है, और यह 2 है।
इसलिए, जब -8 को 5 से विभाजित किया जाता है तो शेष 2 होता है।
(ii) यदि दो संख्याएँ ' a1 ' तथा 'a2 ' n से पूर्णतः विभाज्य हैं। तो उनका योग, अंतर तथा गुणनफल भी n से पूर्णतः विभाज्य होगा।
अर्थात्, यदि ' a1 ' तथा ' a2 ' n से विभाज्य हैं, तो
(a) a1 + a2 भी n से विभाज्य है।
(b) a1 - a2 भी n से विभाज्य है।
(c) a1 × a2 भी n से विभाज्य है।
उदाहरण के लिए: 12, 3 से विभाज्य है और 21 भी 3 से विभाज्य है।
अतः, उनका योग भी 3 से विभाज्य होगा अर्थात
12 + 21 = 33
अंतर भी 3 से विभाज्य है
12 - 21 = - 9 और
गुणनफल भी 3 से विभाज्य है
12 × 21 = 252
शेषफल प्रमेय की सहायता से घातों का शेषफल ज्ञात करना
हम इस अवधारणा को निम्नलिखित उदाहरणों का उपयोग करके समझेंगे
उदाहरण 1: यदि 7 25 को 6 से विभाजित किया जाए तो शेषफल क्या होगा ?
हल: यदि 7 को 6 से विभाजित किया जाए तो शेषफल 1 होगा। इसलिए यदि 7 25 को 6 से विभाजित किया जाए तो शेषफल 1 होगा (क्योंकि 7 25 = 7 × 7 × 7… 25 बार। इसलिए शेषफल = 1 × 1 × 1…. 25 बार = 125)।
उदाहरण 2: यदि 363 को 14 से विभाजित किया जाए तो शेषफल क्या होगा ।
हल: यदि 33 को 14 से विभाजित किया जाए तो शेषफल - 1 होगा। इसलिए 363 को (33)21 के रूप में लिखा जा सकता है ।
इसलिए शेषफल (- 1) 21 = - 1 होगा
। यदि भाजक 14 है तो शेषफल - 1 का अर्थ 13 है। पैटर्न विधि से (14 - 1 = 13)।
 |
Download the notes
संख्यात्मक प्रणाली: शेषफल खोजना
|
Download as PDF |
Download as PDF
शेषफल ज्ञात करने में द्विपद प्रमेय का अनुप्रयोग
- किसी भी अभिव्यक्ति का द्विपद विस्तार
- (a + b) n = n C o a n + n C 1 a n-1 × b 1 + n C 2 × a n-2 × b 2 ..... + n C n-1 × a 1 × b n-1 + n C n × b n
- जहाँ n C o , n C 1 , n C 2 , .... सभी को द्विपद गुणांक कहा जाता है
- सामान्यतः, n C r = n!/r!(n - r)!
कुछ मौलिक निष्कर्ष हैं जो याद रखने पर सहायक होते हैं:
(a) (n + 1) पद हैं।
(b) विस्तार के पहले पद में केवल a है।
(c) विस्तार के अंतिम पद में केवल b है।
(d) अन्य सभी (n - 1) पदों में a और b दोनों होते हैं।
(e) यदि (a + b) n को a से विभाजित किया जाता है, तो शेषफल b n होगा , जिससे b n < a.
उदाहरण : यदि 7 25 को 6 से विभाजित किया जाए तो शेष क्या होगा ?
- हल: (7) 25 को (6 + 1) 25 लिखा जा सकता है ।
- अतः द्विपद विस्तार में, सभी प्रथम 25 पदों में 6 होंगे।
- 26वाँ पद (1) 25 है । अतः विस्तार 6x + 1 लिखा जा सकता है।
- 6x सभी प्रथम 25 पदों का योग दर्शाता है।
- चूँकि उनमें से प्रत्येक 6 से विभाज्य है, इसलिए उनका योग भी 6 से विभाज्य है, और इसलिए, इसे 6x लिखा जा सकता है, जहाँ x कोई भी प्राकृतिक संख्या है।
- अतः 6x + 1 को 6 से भाग देने पर शेषफल 1 बचता है।
(अथवा)- जब 7 को 6 से भाग दिया जाता है तो शेष 1 बचता है। अतः जब 7 25 को 6 से भाग दिया जाता है तो शेष 125 = 1 बचेगा ।
 |
Take a Practice Test
Test yourself on topics from Bank Exams exam
|
Practice Now |
Practice Now
महत्वपूर्ण बिंदु
- लगातार पाँच पूर्ण संख्याओं का योग हमेशा 5 से विभाज्य होता है।
- किसी भी विषम संख्या के वर्ग को 8 से भाग देने पर शेष 1 बचेगा
- किसी भी तीन क्रमागत प्राकृतिक संख्याओं का गुणनफल 6 से विभाज्य होता है।
- किसी भी नौ क्रमागत संख्याओं के गुणनफल का इकाई अंक सदैव शून्य होता है।
- किसी भी प्राकृतिक संख्या n के लिए, 10n - 7, 3 से विभाज्य है।
- कोई भी तीन अंकों वाली संख्या जिसके सभी अंक समान हों, सदैव 37 से विभाज्य होगी।
The document संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams is a part of the Bank Exams Course Quantitative Aptitude/संख्यात्मक योग्यता.
All you need of Bank Exams at this link: Bank Exams
|
223 docs|265 tests
|
FAQs on संख्यात्मक प्रणाली: शेषफल खोजना - Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
| 1. संख्यात्मक प्रणाली में शेषफल क्या होता है? |  |
| 2. शेषफल कैसे निकाला जाता है? | |
Ans. शेषफल निकालने के लिए, सबसे पहले आपको उस संख्या को विभाजित करना होता है जिसे आप विभाजित कर रहे हैं। फिर, उस संख्या को उसके गुणांक (quotient) से गुणा करें और अंतिम परिणाम को मूल संख्या से घटाएं। यह प्रक्रिया आपको शेषफल देगी।
| 3. क्या शेषफल हमेशा सकारात्मक होता है? | |
Ans. हाँ, शेषफल हमेशा सकारात्मक या शून्य होता है। जब हम किसी संख्या को विभाजित करते हैं, तो शेषफल उस संख्या से कम होता है और कभी भी नकारात्मक नहीं होता।
| 4. शेषफल का उपयोग किस प्रकार के गणित में किया जाता है? | |
Ans. शेषफल का उपयोग विभाजन, संख्यात्मक विश्लेषण, और गणितीय समस्याओं में किया जाता है। यह विशेष रूप से संख्याओं के गुणन और विभाजन में महत्वपूर्ण है, जैसे कि लघुतम समापवर्तक (LCM) और महत्तम समापवर्तक (GCD) निकालने में।
| 5. क्या शेषफल को किसी अन्य संख्या प्रणाली में भी लागू किया जा सकता है? | |
Ans. हाँ, शेषफल को विभिन्न संख्या प्रणालियों में लागू किया जा सकता है, जैसे कि द्विआधारी (binary) या अष्टाधारी (octal) संख्या प्रणाली। हर प्रणाली में, शेषफल निकालने की प्रक्रिया समान रहती है, लेकिन संख्याओं की प्रणाली के अनुसार परिणाम भिन्न हो सकते हैं।
Related Exams
About this Document
4.70/5
Rating
Mar 29, 2025
Last updated
Document Description: संख्यात्मक प्रणाली: शेषफल खोजना for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation.
The notes and questions for संख्यात्मक प्रणाली: शेषफल खोजना have been prepared according to the Bank Exams exam syllabus. Information about संख्यात्मक प्रणाली: शेषफल खोजना covers topics
like शेष क्या है?, गुणनफल का शेषफल ज्ञात करना (शेषफल व्युत्पन्न प्रमेय), शेषफल प्रमेय की सहायता से घातों का शेषफल ज्ञात करना, शेषफल ज्ञात करने में द्विपद प्रमेय का अनुप्रयोग, महत्वपूर्ण बिंदु and संख्यात्मक प्रणाली: शेषफल खोजना Example, for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for संख्यात्मक प्रणाली: शेषफल खोजना.
Introduction of संख्यात्मक प्रणाली: शेषफल खोजना in English is available as part of our Quantitative Aptitude/संख्यात्मक योग्यता
for Bank Exams & संख्यात्मक प्रणाली: शेषफल खोजना in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course.
Download more important topics related with notes, lectures and mock test series for Bank Exams
Exam by signing up for free. Bank Exams: संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
Description
Full syllabus notes, lecture & questions for संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams - Bank Exams | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude/संख्यात्मक योग्यता | Best notes, free PDF download
Information about संख्यात्मक प्रणाली: शेषफल खोजना
In this doc you can find the meaning of संख्यात्मक प्रणाली: शेषफल खोजना defined & explained in the simplest way possible. Besides explaining types of
संख्यात्मक प्रणाली: शेषफल खोजना theory, EduRev gives you an ample number of questions to practice संख्यात्मक प्रणाली: शेषफल खोजना tests, examples and also practice Bank Exams
tests
Related Searches
Important questions
,MCQs
,Free
,Summary
,Sample Paper
,video lectures
,Semester Notes
,Previous Year Questions with Solutions
,mock tests for examination
,Viva Questions
,Exam
,practice quizzes
,past year papers
,study material
,संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,shortcuts and tricks
,ppt
,संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,Extra Questions
,Objective type Questions
,संख्यात्मक प्रणाली: शेषफल खोजना | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
;
Additional Information about संख्यात्मक प्रणाली: शेषफल खोजना for Bank Exams Preparation
संख्यात्मक प्रणाली: शेषफल खोजना Free PDF Download
The संख्यात्मक प्रणाली: शेषफल खोजना is an invaluable resource that delves deep into the core of the Bank Exams exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the संख्यात्मक प्रणाली: शेषफल खोजना now and kickstart your journey towards success in the Bank Exams exam.
Importance of संख्यात्मक प्रणाली: शेषफल खोजना
The importance of संख्यात्मक प्रणाली: शेषफल खोजना cannot be overstated, especially for Bank Exams aspirants.
This document holds the key to success in the Bank Exams exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
संख्यात्मक प्रणाली: शेषफल खोजना Notes
संख्यात्मक प्रणाली: शेषफल खोजना Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to संख्यात्मक प्रणाली: शेषफल खोजना.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, संख्यात्मक प्रणाली: शेषफल खोजना Notes on EduRev are your ultimate resource for success.
संख्यात्मक प्रणाली: शेषफल खोजना Bank Exams Questions
The "संख्यात्मक प्रणाली: शेषफल खोजना Bank Exams Questions" guide is a valuable resource for all aspiring students preparing for the
Bank Exams exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study संख्यात्मक प्रणाली: शेषफल खोजना on the App
Students of Bank Exams can study संख्यात्मक प्रणाली: शेषफल खोजना alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the संख्यात्मक प्रणाली: शेषफल खोजना,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of संख्यात्मक प्रणाली: शेषफल खोजना is prepared as per the latest Bank Exams syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily